Класифікація диф. р-нь першого порядку та приклади

 Сьогодні поговоримо про те як класифікувати диференціальні рівняння (ДР) першого порядку, загальні означення та розберемо готові приклади на ряд ДР першого порядку. Класифікація потрібна для того, щоб далі розуміти в який спосіб те чи інше рівняння можна розв'язати. Без розуміння, "що за диференціальне рівняння Вам задано?" буде важко відшукати його загальний чи частинний розв'язок.
Що таке загальний і частинний розв'язок ДР, загальний інтеграл ДР та частинний інтеграл Ви можете пригадати з наступної теорії:

Щоб швидко класифікувати диференціальне рівняння та знати як його обчислювати ми вибрали гарні таблиці з літератури, з яких Ви швидко можете знайти відповіді на питання:
Що таке найпростіше диференціальне рівняння?
Які ДР називають рівняннями з віокремлюваними змінними, а які з відокремленими?
Який вигляд мають однорідні ДР?
В чому різниця між однорідними та неоднорідними ДР?
Яке ДР називають рівнянням Бернуллі?
Як перевірити чи маємо рівняння в повних диференціалах?
На ці питання Ви повинні вміти відповідати, бо їх часто задають на практичних та тестах, і за відповіддю викладач швидко може перевірити наскільки добре Ви знаєте основи ДР. Тому перегляньте та запам'ятайте вміст наступних таблиць, а далі уважно розберіть приклади, що ми для Вас підготували.

Класифікація ДР першого порядку

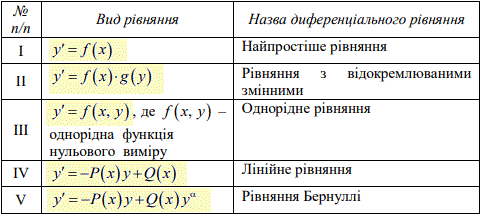
Таблиці 2, 3. Види диференціальних рівнянь

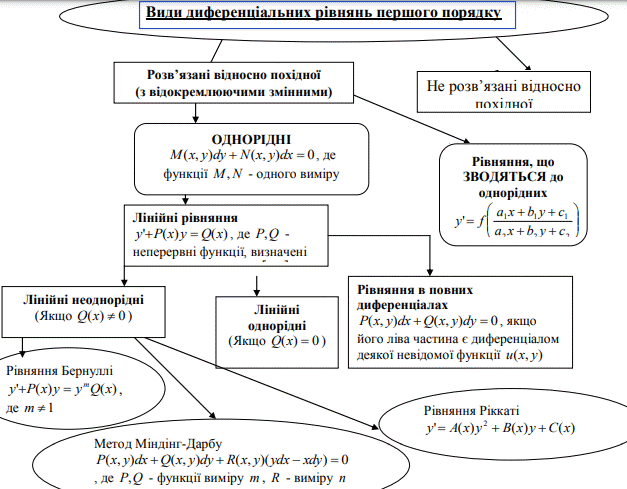
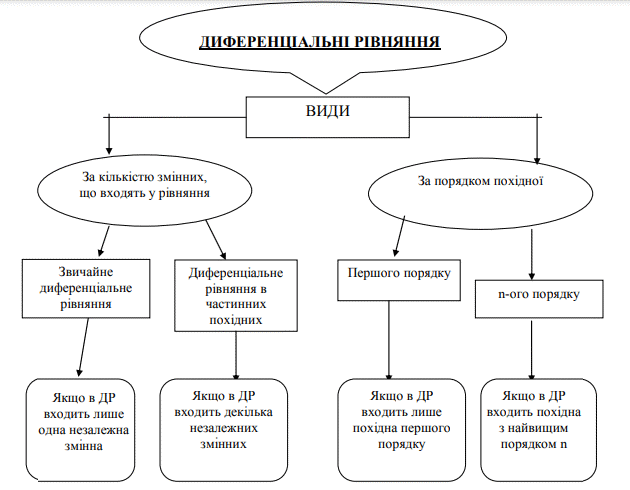
Найпростіші диференціальні рівняння

Приклад 1. Знайти розв'язок ДР
y'=4x
Розв'язування: Маємо найпростіше ДР першого порядку.
При інтегруванні обох її частин отримаємо
y=4x²/2+C=2x²+C - загальний розв'язок ДР.
де C - довільна стала.

Приклад 2. Знайти розв'язок ДР
y'=8^x
Розв'язування: З вигляду р-ня робимо висновок що це найпростіше ДР першого порядку.
Похідну y' замінюємо приростом функції до приросту аргументу y'=dy/dx, розділяємо змінні та інтегруємо

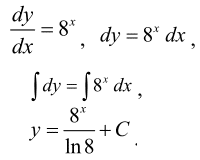
Не забувайте, що невизначений інтеграл рівний значенню інтегралу + стала С.

Приклад 3. Розв'язати задачу Коші
y'=cos(x), y(0)=π.
Розв'язування: Інтегруємо найпростіше ДР першого порядку.

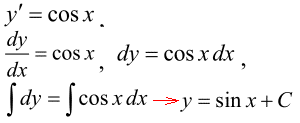
Записуємо y=sin(x)+C - загальний розв'язок ДР.
Обчислимо розв'язок задачі Коші
y(0)=Pi.->π=sin(0)+C,
π=0+C,
C=π.
Підставивиши C=π в загальний розв'язок ДР, отримаємо
y=sin(x)+π - частинний розв'язок заданого ДР.
І подібних умов можна навести тисячі.
При інтегруванні лівої частини отримаєте функцію, а праву слід звести до одного з відомих табличних інтегралів +С.
Ось і вся методика обчислення найпростіших ДР.

Рівняння з відокремлюваними змінними

Приклад 4. Знайти загальний розв'язок ДР
y'=x*(y-1)
Розв'язування: Маємо ДР з відокремлюваними змінними, оскільки права сторона має вигляд f(x)*g(y)
Замінюємо y'=dy/dx, розділяємо змінні та інтегруємо

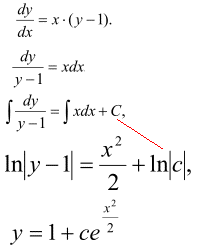
де C=ln(c) - довільна стала.
При розв'язуванні ДР часто сталу С вносять під логарифм чи експоненту, перепепозначають і вже оперують новою сталою.
В такий спосіб добиваються компактного вигляду загального розв'язку ДР та простоти обчислень.

Приклад 5. Знайти розв'язок задачі Коші

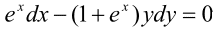
y(0)=2.
Розв'язування: Маємо ДР з відокремлюваними змінними.
В другому рядку формул розділили змінні, тому таке р-ня вже називається - ДР з відокремленими змінними.

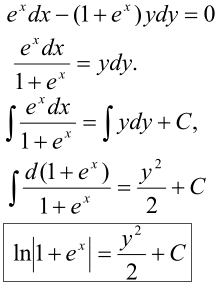
Останніій запис не містить явно вираженої функції y(x) - тому такий запис розв'язку називають загальний інтеграл ДР.
Розв'яжемо задачу Коші:
y(0)=2
Підставляємо в загальний інтеграл ДР
ln(1+1)=2²/2+C,
C=ln(2)-4/2=ln(2)-2.
Заміняєємо сталу в загальниому інтегралі ДР та отримаємо
ln(|1+ex|)=y2/2+ln(2)-2 - частинний інтеграл диференціального рівняння.
Розглянемо, ще один приклад де в результаті інтегрування отримаємо загальний інтеграл ДР.

Приклад 6. Розв'язати диференціальне рівняння
x+y*y'=0.
Розв'язування: Бачимо, що можемо розділити змінні, тому таке рівняння є ДР з відокремлюваними змінними.
При інтегруванні обох її частин отримаємо

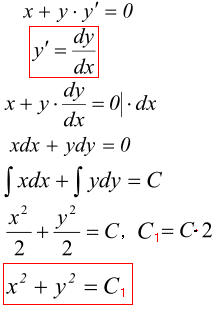
y=4x²/2+C=2x²+C -загальний розв'язок ДР.
 C - довільна стала.

Приклад 7. Зінтегрувати рівняння
(1+x^2)y*dx+(1+y^2)x*dy=0
Розв'язування: Розділяємо змінні в ДР та інтегруємо.
При інтегруванні обох її частин отримаємо логарифми, які групуємо за правилом суми логарифмів

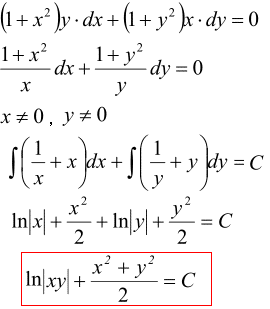
Остання формула містить загальний інтеграл ДР.
(не плутати з загальним розв'язком y(x)=...).
Слід відзначити, що всюди потрібно перевіряти вирази на які ділимо.
Так тут виконували ділення на "x, y", тому слід перевірити чи пара x=0, y=0 не перетворює задане ДР в тотожність.
(1+0)*0*dx+(1+0)*0*dy=0.
Таким чином, точка x=0,y=0 - є особливим розв'язком диференціального рівняння.

Приклад 8. Знайти розв'язок ДР
y'=(4x+y+5)²
Розв'язування: Дане рівняння є звідним до рівнянь з відокремлюваними змінними.
Для цього слід ввести заміну змінних
z=4x+y або z=4x+y+5.
Вибираємо першу з них, диференціюємо, покладаючи z, y за функції, а x -за змінну.
Далі виражаємо y', підставляємо в рівняння, після чого розділяємо змінні та інтегруємо

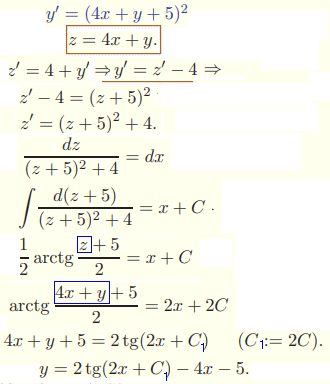
Остання формула має явний вигляд функції y тому це загальний розв'язок ДР.
Тут ми ділили на (z+5)²+4, але оскільки цей вираз завжди додатний, то перевіряти чи він буде особливим розв'язком ДР немає змісту.
В наступних уроках продовжимо знайомитися з методами розв'язування ДР та різними алгоритмами, що дозволяють це робити швидко та правильно.