Сьогодні продовжимо розв'язувати ірраціональні рівняння із ЗНО підготовки та розберемо приклади в яких явно маємо квадратні рівняння під коренями, або в процесі розкриття коренів отримуємо квадратні рівняння. Такі завдання зустрічалися і раніше, але вони були не важкими та їх не об'єднували в окрему статтю. Деякі приклади увійшли в наступну публікацію, де розв'язані складні ірраціональні рівняння з параметром.
Приклад 12.31 Розв'язати рівняння 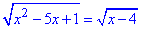 Обчислення: Для коренів квадратних записуємо ОДЗ:
Обчислення: Для коренів квадратних записуємо ОДЗ:
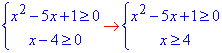
Далі підносимо обидві частини до квадрату та розписуємо
x2-5x+1=x-4,
x2-5x+1-x+4=0,
x2-6x+5=0,
За теоремою Вієта знаходимо розв'язки квадратного рівняння:
x1=1 (не належить ОДЗ) і x2=5.
Відповідь: 5.
Хто вивчає математичні пакети як Мaple, Mathcad, MatLab ... то може не тільки розв'язувати в них задані рівняння, але й будувати графіки функцій. Для розглянутого прикладу побудуємо різницю коренів на проміжку від 4 до 10 в пакеті Мaple та розв'яжемо рівняння.
Щоб це зробити можете скористатися кодом
> restart;
> solve(sqrt(x^2-5*x+1)-sqrt(x-4)=0,x);
> plot(sqrt(x^2-5*x+1)-sqrt(x-4),x=4..10,thickness=2,color=blue);
В результаті компіляцї отримаєте розв'язки та графік
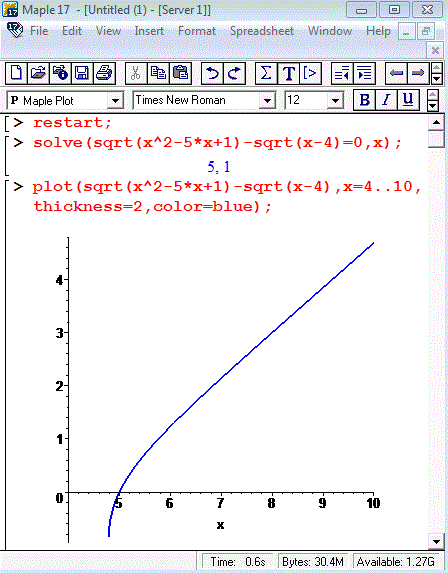
Бачимо, що математичні пакети теж можуть давати зайві корені. Щоб цього уникнути вони мають ряд команд, щоб врахувати області визначення і т.д., але про це піде мова в інших уроках.
Приклад 12.32 Розв'язати рівняння 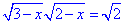 Обчислення: Записуємо систему нерівностей для ОДЗ:
Обчислення: Записуємо систему нерівностей для ОДЗ:
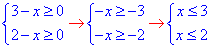
звідси x≤2.
Далі без змін підносимо обидві частини до квадрату
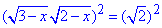
(3-x)(2-x)=2,
6-3x-2x+x2-2=0,
x2-5x+4=0,
За формулою Вієта отримаємо:
x1=1 і x2=4 (не належить ОДЗ).
Відповідь: 1.
Приклад 12.33 Розв'язати рівняння 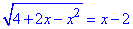 Обчислення: Підкоренева функція не повинна приймати від'ємних значень + права сторона також.
Обчислення: Підкоренева функція не повинна приймати від'ємних значень + права сторона також.
З цього маємо дві нерівності для ОДЗ:
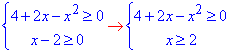
Для розкриття ірраціональності обидві сторони підносимо до квадрату
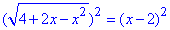
та розписуємо
4+2x-x2=x2-4x+4,
x2+x2-4x-2x-4+4=0,
2x2-6x=0,
2x(x-3)=0,
x1=0 (не належить ОДЗ) і x2=3,
Відповідь: 3.
Приклад 12.34 Розв'язати рівняння 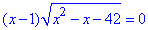 У відповідь записати модуль різниці коренів.
У відповідь записати модуль різниці коренів.
Обчислення: Встановлюємо ОДЗ:
x2-x-42≥0, (x+1)(x-7)≥0,
звідси x∈(-∞;-6] ∪[7;+∞).
Далі шляхом піднесення до квадрату позбуваємося радикала
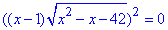
(x-1)2(x2-x-42)=0,
(x-1)2(x+6)(x-7)=0,
x1=1 (не належить ОДЗ), x2=-6 і x3=7.
Знайдемо модуль різниці коренів x2=-6 і x3=7:
|x2-x3|=|-6-7|=|-13|=13.
Відповідь: 13.
Приклад 12.35 Розв'язати рівняння 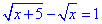 Обчислення: Схема розрахунків не змінюється і є універсальною для всіх ірраціональних рівнянь, тому постарайтеся її не забути.
Обчислення: Схема розрахунків не змінюється і є універсальною для всіх ірраціональних рівнянь, тому постарайтеся її не забути.
Визначаємо область визначення:
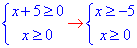
звідси x≥0.
Позбуваємося ірраціональності та розв'язуємо рівняння
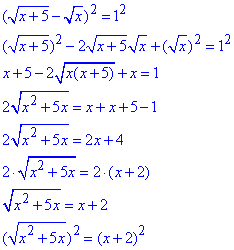
x2+5x=x2+4x+4,
x2+5x-x2-4x=4,
x=4.
Відповідь: 4.
Приклад 12.36 Розв'язати рівняння 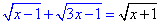 Обчислення: Складаємо нерівності для ОДЗ:
Обчислення: Складаємо нерівності для ОДЗ:
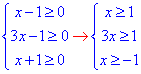
звідси сумарно x≥1.
Щоб позбутися коренів підносимо рівняння до квадрату
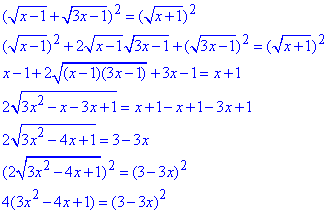
Розписуємо до квадратного рівняння
12x2-16x+4=9-18x+9x2,
12x2-9x2-16x+18x+4-9=0,
3x2+2x-5=0
та через дискримінант знаходимо його розв'язки
D=22-4•3•(-5)=4+60=64=(±8)2,
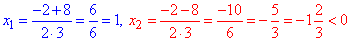
(другий не належить ОДЗ).
Відповідь: 1.
Приклад 12.41 Розв'язати систему рівнянь
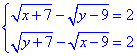 У відповідь записати найбільше зі значень x0 або y0, де пара (x0;y0) – розв'язок системи.
У відповідь записати найбільше зі значень x0 або y0, де пара (x0;y0) – розв'язок системи.
Обчислення: Маємо систему ірраціональних рівнянь в якому змінні "ікс, ігрик" містяться під коренями квадратними, причому в лінійних залежностях. Причому змінні розділені, тому можемо визначити область визначення для кожної змінної:
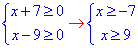
звідси x≥9;
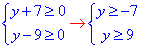
звідси y≥9.
Далі один з коренів (зі знаком мінус) переносимо за знак рівності та методом підняття до квадрату починаємо розкривати корені
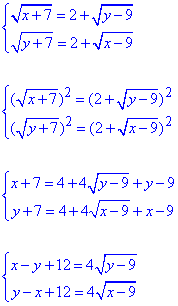
Додамо обидва рівняння і результат запишемо у першому рівнянні.
Далі одне з рівнянь з двома кореневими функціями повторно підносимо до квадрату та спрощуємо:
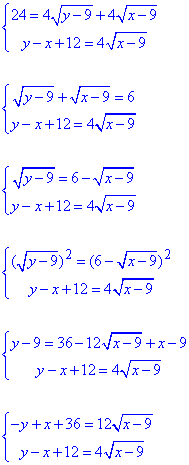
Додамо обидва рівняння і результат запишемо у першому рівнянні. Далі це рівняння підносимо до квадрату та визначаємо "ікс", а далі "ігрик" з другого:
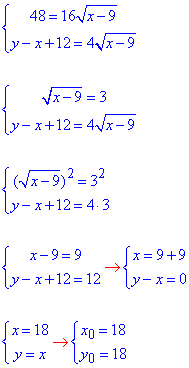
Перш за все запам'ятайте, що перед піднесенням до квадрату слід рознести корені квадратні по різні сторони від знаку рівності.
Відповідь: 18.
Приклад 12.42 Розв'язати рівняння
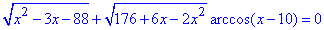
Обчислення: В рівнянні під коренем маємо дві квадратичні залежності та арккосинус.
З цього слідує, що отримаємо три нерівності для області визначення:
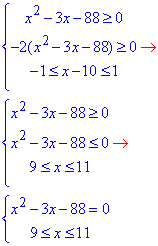
Отже, задані нерівності рівносильні рівнянню
x2-3x-88=0,
де змінна повинна належати проміжку 9≤x≤11.
Обчислюємо дискримінант
D=(-3)2-4•1•(-88)=9+352=361=(±19)2
та корені квадратного рівняння
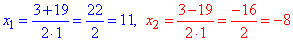
(другий не належить ОДЗ), x=11.
Отримана відповідь є одночасно розв'язком ОДЗ і коренем заданого рівняння.
Відповідь: 11.
Наведені завдання вимагають добрих знань властивостей кореневих функцій та ефективних способів для обчислення квадратних рівнянь. Схеми розрахунків для ірраціональних рівнянь давалися раніше і є досить простими. В наступній статті розв'яжемо кілька рівнянь з параметрами, а далі перейдемо до обчислень ірраціональних нерівностей.


