Сьогодні розберемо перші завдання з курсу ЗНО підготовки, які методом нескладних перетворень можна звести до показникових рівнянь з однаковими основами:
af(x)=ab,
подальші обчислення зводяться до прирівняння показників, і якщо немає обмежень на ОДЗ функції f(x) у вsдповідь записуємо корені рівняння f(x)=b.
Необхідний мінімум властивостей показникових функцій, якими Ви повинні вміти оперувати наведено на рисунку нижче
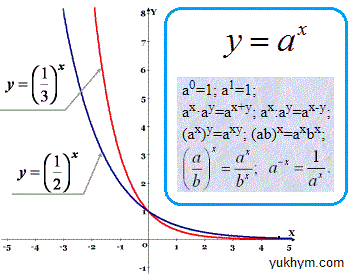
Далі ідуть пояснення до прикладів із ЗНО тестів.
Приклад 14.1 Розв'язати рівняння 4x=8.
А | Б | В | Г | Д |
1/2 | 2/3 | 3/2 | 2 | 32 |
Розв'язування: Маємо показникове рівняння найпростішого типу, яке розв’язуємо методом зведення до однакової основи обох частинах рівняння:
4x=8,
(22)x=8,
22x=23
далі при рівних основах прирівняємо показники:
2x=3, звідси x=3/2.
Відповідь: 3/2 – В.
Приклад 14.2 Розв'язати рівняння 5x-9=5 і 3x-3=0 та вказати суму їх коренів.
А | Б | В | Г | Д |
0 | 1 | 8 | 9 | 11 |
Розв'язування: Бачимо, що основи в рівнянь рівні між собою, тому прирівнюємо степені та знаходими "ікси"
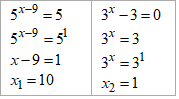
x1+x2=10+1=11 – сума коренів.
Відповідь: 11 – Д.
Приклад 14.3 Розв'язати рівняння (1/2)x+2=42x і 43x+1=8-2x-1 та вказати інтервал, який містить їх корені. 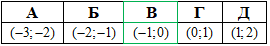
Розв'язування: Алгоритм обчислень один і той самий: через елементарні перетворення перетворюємо основи до спільної для обох сторін рівняння, після чого прирівнюємо показники.
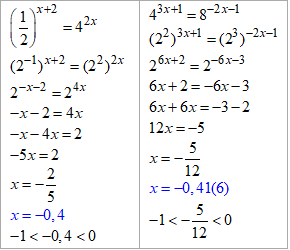
Далі перевіряємо, якому із запропонованих у ЗНО відповідях інтервалів належать обидва розв'язки: (-1,0).
Відповідь: (-1,0) – В.
Приклад 14.9 Розв'язати рівняння 6^(x+1)=3^(x+1) і 2^(x-5)=8^(x-5) і знайти суму їх коренів.
А | Б | В | Г | Д |
4 | -4 | 5 | -5 | 53 |
Розв'язування: Даний тип показникових рівнянь розв'язуємо методом ділення однієї з частин рівняння на менший з виразів, що містить "ікси" в показнику.
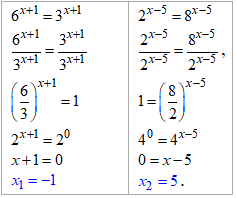
За властивістю показникових функцій одиницю всюди заміняйте основою в нульовому степені.
x1+x2=-1+5=4 – сума коренів.
Відповідь: 4 – А.
Приклад 14.11 Знайти суму коренів рівняння 5^2x-6•5^x+5=0.
А | Б | В | Г | Д |
1 | 0 | -6 | 6 | -5 |
Розв'язування: Перепишемо рівняння у вигляді
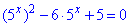
та зведемо до квадратного заміною змінних 5x=t, де t>0:
t2-6t+5=0.
За формулами Вієта:
t1+t2=6 – сума коренів квадратного рівняння:
t1•t2=5 – їх добуток.
Підбираємо розв'язки
t1=1 і t2=5.
повертаємося до заміни t=5x та обчислюємо показникове рівняння
5x=1,
5x=50,
x1=0.
5x=5
5x=51,
x2=1.
корені рівняння x1=0 і x2=1
x1+x2=1 – шукана сума.
Відповідь: 1 – А.
Приклад 14.12 Встановити кількість коренів рівняння
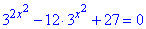
А | Б | В | Г | Д |
Жодного | один | два | три | чотири |
Розв'язування: Перетворимо перший доданок за властивостями показників
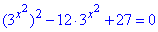
Бачимо, яку заміну змінних слід застосувати:
3^x2=t (де t>0)
щоб звести задане рівняння до квадратного
t2-12t+27=0.
За формулами Вієта запишемо:
t1+t2=12 – суму коренів р-ня;
t1•t2=27 – їх добуток.
Звідси отримаємо
t1=3 і t2=9 – розв'язки квадратного рівняння.
Повертаємося до заміни t=3^x2 та розписуємо прості показникові рівняння:
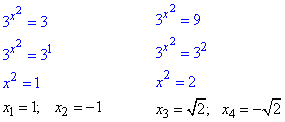
x1=1; x2=-1; x3=√2; x4=-√2 – корені рівняння, їх кількість = 4.
Відповідь: чотири – Д.
Приклад 14.28 Установити відповідність між рівняннями (1–4) та сумами їх коренів (А–Д).
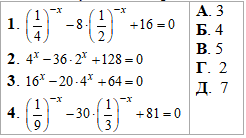
Рівняння зводимо до простих показникових методом виділення НСК, який рівний 2x для усіх заданих прикладів. Після цього, множники при 2x переносимо в праву сторону та спрощуємо.
Весь хід розрахунків детально розписаний далі:
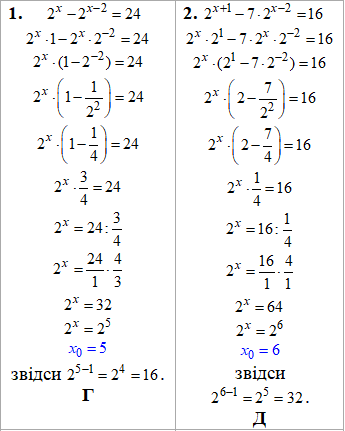

Приклад 14.29 Розв'язати рівняння
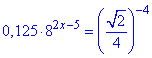
Розв'язування: Зведемо дроби до спільної основи =2 в певному степені:
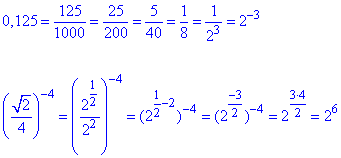
В такий спосіб отримаємо просте показникове рівняння відносно змінної x.
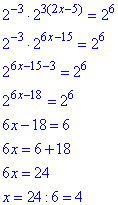
Його розв'язок рівний 4.
Відповідь: 4.
Приклад 14.42 Розв'язати рівняння
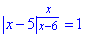
У відповідь записати найбільший корінь рівняння.
Розв'язування: Маємо змінну під модулем у степені рівному дробовій функції, а права частина рівна нулю. Для показникових функцій це рівносильно тому, що або основа рівна 1 або показник =0.
Спершу обмежуємо множину розв'язків умовою, що знаменник в показнику не дорівнює нулю:
ОДЗ: x-6≠0, x≠6.
Далі виписуємо два рівняння та розв'язуємо їх:
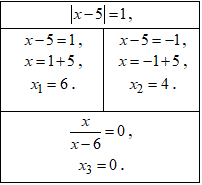
Дехто з учнів без вагань запише x1=6 , як найбільший розв'язок завдання серед знайдених.
Але Ви не перевіряли ОДЗ, або можливо при розв'язуванні опустили цю процедуру.
ОДЗ виключає даний корінь x≠6.
Тому x2=4 – найбільший корінь рівняння.
Якщо не виписуєте ОДЗ, тоді після розрахунків виконуйте підстановку та перевіряйте чи отримуєте тотожність, чи особливість.
На ЗНО тестах є багато завдань, де Ви можете добре обчислити, але неправильно трактувати, що від Вас вимагають і вписати помилкову відповідь. Про це у нас є окрема стаття, яка якраз вчить на чому Вас можуть підловити на тестах, контрольних, олімпіадах.
Відповідь: 4.
Попереду ще десятки розв'язаних прикладів, які навчать обчислювати показникові рівняння при різних основах, познайомлять з рівняннями звідними до квадратних та іншими методами розкриття показникових рівнянь.


