Знаходження рівняння прямої регресії та інтервалу довіри

З другого індивідуального завдання з теорії ймовірностей Ви навчитеся знаходити рівняння прямої регресії двох ознак та знаходити межі інтервалу довіри. Ці дві величини між собою не пов'язані, однак на практиці в контрольних чи тестах зустрічаються одночасно.

Практикум з ТМС. Варіант-8

Завдання 1. Зв'язок між ознаками Х і Y генеральної сукупності задається таблицею:

Записати вибіркове рівняння прямої регресії Y на X.
Розв'язання: Для побудови прямої регресії Y на X слід спершу знайти середнє значення кожної з ознак:

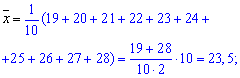
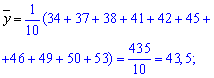
Далі суму їх попарних добутків

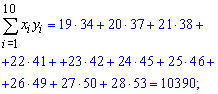
та квадратів значень ознаки X

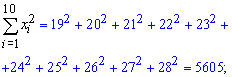
Після цього можемо порахувати самі коефіцієнти, що фігурують в рівнянні регресії

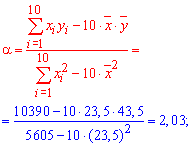
Ну і сама легша частина - це все підставити у рівняння y=2,02*x-4,205. З вигляду формул бачимо, що надзвичайно складних операцій виконувати тут не приходиться. Однак і тут багато хто з Вас умудряється наробити помилок.
Для підтвердження лінійного зв'язку між ознаками Y на X слід ще знайти вибірковий коефіцієнт кореляції:

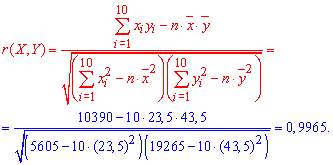
Чим він ближче до одиниці, тим краще лінійна функція описує залежність між ознаками. В нашому випадку вибірковий коефіцієнт кореляції r(X, Y) практично співпадає з одиницею, тому робимо висновок, що припущення про лінійність зв'язку між X і Y правильне. Також r>0, що свідчить про додатний зв'язок між X і Y,є тобто ці випадкові величини збільшуються одночасно.

Завдання 2. Знайти інтервал довіри для оцінки з надійністю γ невідомого математичного сподівання а нормально розподіленої ознаки Х генеральної сукупності:

а) якщо γ=0,96, генеральне середнє квадратичне відхилення σ=5,0, вибіркове середнє =28,0, а обсяг вибірки n=25;
б) якщо γ=0,99, підправлене середнє квадратичне відхилення s=12,0, вибіркове середнє =65,0, а обсяг вибірки n=16.

Розв'язання: а) З рівняння за допомогою функції Лапласа методом інтерполяції із сусідніх значень знаходимо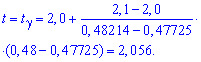

Межі інтервалу довіри знаходимо із формулами:

Записуємо інтервал довіри

з надійністю

б) Оскільки n=16<30 і середнє квадратичне відхилення невідоме, то для знаходження меж інтервалу довіри використаємо формулу
,
де значення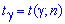шукаємо за допомогою таблиць (розподіл Ст'юдента):

Отже, інтервал довіри рівний з надійністю .

Завдання 3. Знайти інтервал довіри для оцінки з надійністю γ=0,99 невідомого середнього квадратичного відхилення σ нормально розподіленої ознаки Х генеральної сукупності, якщо обсяг вибірки n=35, а підправлене середнє квадратичне відхилення s=10,3.
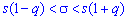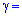Розв'язання: Задача зводиться до відшукання інтервалу довіри , який покриває з заданою надійністю 0,99.
За таблицею функції q знаходимо

Шуканий інтервал довіри лежить в межах

або

Дочитайте відповіді до кінця і теорія ймовірності стане для Вас зрозуміліша і доступна.