Відповіді до контрольної роботи з теорії ймовірності допоможуть студентам перших курсів, що вивчають математичні дисципліни. Завдання охоплюють багато теоретичного матеріалу, а обґрунтування їх розв'язання стане в нагоді кожному студенту.
Завдання 1.Куб, всі грані якого замальовані, розпиляний на 1000 кубиків однакового розміру. Визначити ймовірність того, що кубик, витягнутий навмання, матиме :
- а) одну замальовану грань;
- б) дві замальовані грані.
Обчислення: Якщо куб розпиляти на кубики однакового розміру, то всі грані будуть поділені на 100 квадратів. (Приблизно як на малюнку)
Далі за умовою кубик повинен мати одну замальовану грань – це означає, що кубики повинні належати зовнішній поверхні, але не лежати на ребрах куба (2 замальовані поверхні) і не на кутах – мають три поверхні.
Отже шукана кількість рівна добутку 6 граней на кількість кубиків в квадраті розміром 8*8.
6*8*8=384 – кубики з 1 замальованою поверхнею.
Ймовірність рівна кількості сприятливих подій до загальної їх кількості P=384/1000=0,384.
б) Дві замальовані грані мають кубики по ребрах без вершин куба. На одному ребрі буде 8 таких кубиків. Всього в кубі 12 ребер, тому дві замальовані грані матимуть
8*12=96 кубиків.
А ймовірність витягнути їх серед 1000 всіх рівна
P=96/1000=0,096.
Завдання 2. На однакових картках написані букви А, А, А, Н, Н, С. Яка ймовірність того, що випадково розмістивши картки в ряд, отримаємо слово АНАНАС?
Обчислення: Потрібно розмірковувати завжди від того, що відомо. Дано 3 букви А, 2-Н,та 1 – С, всього їх 6. Почнемо вибирати букви для слова "ананас". Першою йде буква А, її можемо вибрати 3 способами із 6, бо є 3 букви А серед 6 відомих. Тому ймовірність витягнути першою А рівна
P1=3/6=1/2.
Друга буква Н, але слід не забувати, що після того як витягнули А залишається 5 букв для вибору. Тому ймовірність витягнути під 2 номером Н рівна
P2=2/5.
Наступну А ймовірність витягнути серед 4, що лишилося
P3=2/4.
Далі Н можна витягнути з ймовірністю
P4=1/3.
Чим ближче до кінця тим більша ймовірність, і вже А можемо витягнути при
P5=1/2.
Після цього залишається одна картка С, тому ймовірність її витягнути рівна 100 процентам або
P6=1.
Ймовірність скласти слово АНАНАС рівна добутку ймовірностей
P=3/6*2/5*2/4*1/3*1/2*1=1/60=0,016(6).
На цьому і базуються подібні завдання із теорії ймовірностей.
Завдання 3. З партії виробів товарознавець навмання вибирає зразки. Ймовірність того, що навмання узятий виріб опиниться вищого сорту рівна 0,8. Знайти ймовірність того, що серед 3 відібраних виробів буде два вироби вищого сорту?
Обчислення: Даний приклад на застосування формули Бернуллі.
p=0,8; q=1-0,8=0,2.
Ймовірність обчислюємо за формулою 
Якщо пояснювати не мовою формул, то потрібно скласти комбінації з трьох подій, дві з яких сприятливі, а одна ні. Це можна записати сумою добутків
Обидва варіанти є рівносильні, тільки перший можемо застосувати в усіх завданнях, а другий в подібних до цього.
Завдання 4. З п'яти стрільців двоє попадають в ціль з ймовірністю 0,6 і троє з ймовірністю 0,4. Що вірогідніше: навмання вибраний стрілець попадає в ціль чи ні?
Обчислення: За формулою повної імовірності визначаємо ймовірність, що стрілець попаде.
P=2/5*0,6+3/5*0,4=0,24+0,24=0,48.
Ймовірність менша P<0,5, отже вірогідніше, що навмання вибраний стрілець не попаде у ціль.
Ймовірність, що не влучить становить
або
P=2/5*(1-0,6)+3/5*(1-0,4)=0,16+0,36=0,52.
Отже, робимо висновок, що вірогідніше стрілець не влучить.
Завдання 5. З 20 студентів, що прийшли на іспит, 10 підготовлені відмінно(знають всі питання), 7 добре(знають по 35 питань), а 3 погано (10 питань). У програмі 40питань. Навмання викликаний студент відповів на три питання квитка. Яка ймовірність того, що він підготовлений на
- а) відмінно;
- б) погано.
Обчислення: Суть задачі полягає в тому, що студент відповів на три питання квитка, тобто на всі що були задані, а от яка ймовірність їх витягнути ми зараз обчислимо.
Знайдемо ймовірність, що студент відповів на три питання. Це буде відношення кількості студентів до всієї групи помножене на ймовірність витягнути білети, що вони знають серед всієї їх кількості
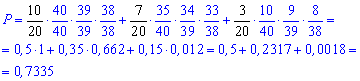
Тепер знайдемо ймовірність, що студент належить групі, що підготовлена на відмінно. Це рівносильно частці першого доданку попередньої ймовірності, до цієї ймовірності
б) Ймовірність, що студент належить групі, що погано підготувалася досить мала і рівна 0,00216.
На цьому завдання виконано. Добре його розберіть та запам'ятайте як обчислювати його, оскільки на контрольних і тестах воно поширене.
Завдання 6. Монету кидають 5 разів. Знайти ймовірність того, що герб падає менше 3 разів?
Обчислення: Ймовірність витягнути герб чи решку рівносильна і рівна 0,5. Менше 3 разів означає, що герб може випасти або 0, або 1, або 2 рази. "Або" завжди в ймовірності в операціях позначається додаванням.
Ймовірності знаходимо за формулою Бернуллі
Оскільки p=q=0,5, то ймовірність рівна
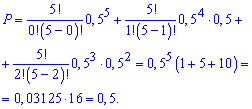
Ймовірність рівна 0,5.
Завдання 7. При штампуванні металевих клем виходить в середньому 90% стандартних. Знайти ймовірність того, що серед 900 клем стандартними будуть не менше 790 і не більше 820 клем.
Обчислення: Обчислення необхідно проводити за інтегральною теоремою Муавра-Лапласа.
Записуємо відомі величини
n=900; p=0,9; q=1-0,9=0,1; k1=790; k2=820.
Ймовірність знаходимо за формулою
де 
інтегральна функція Лапласа
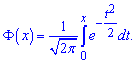
Значення x1, x2 обчислюємо за формулою
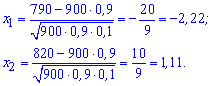
Далі знаходимо ймовірність, що серед 900 клем стандартними будуть не менше 790 і не більше 820 клем
Значення функції Лапласа беремо з таблиці.
Якщо поясните подібні завдання так як тут написано, то за контрольну з ймовірності отримаєте оцінку "відмінно".
