Сьогодні навчимо Вас відновлювати функцію через інтеграл від її повного диференціала. Алгоритм який описує що за чим потрібно робити детально розписаний в наведеній далі статті.
Формула Ньютона-Лейбніца для криволінійного інтеграла від повного диференціала має вигляд
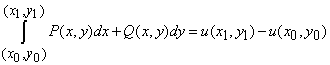 (1)
(1)
де P(x,y) часткова похідна функції u за змінною y,
Q(x,y) часткова похідна функції u за змінною x.
Для її використання необхідно лише переконатися, що часткові похідні P(x,y), Q(x,y) рівні між собою
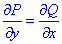
Криволінійний інтеграл 2 роду (1) спрощується,якщо контур інтегрування від точки M0(x0,y0) до M(x,y) по прямій замінити ламаною, що складається з прямих паралельних до осей координат M0M1 та M1M або M0M2 та M2M.
З однієї сторони це дозволяють властивості криволінійних інтегралів. З іншої такий спосіб має практичну вигоду.
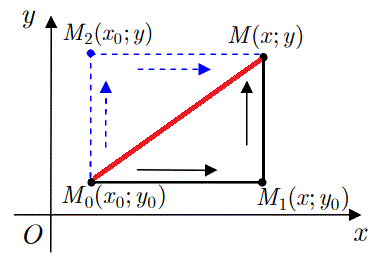
На практиці можемо перетворити в нуль один з диференціалів під інтегралом, якщо інтегрувати вздовж прямих паралельних осям, в замін доводиться інтегрувати вздовж двох відрізків прямих тобто обчислювати суму двох інтегралів. Детальніше про це можете почитати в статті про інтегрування повних диференціалів.
Завдання 1 Знайти функцію z, якщо відомий повний диференціал функції dz=(ydx-xdy)/(3x2-2xy+3y2)

Розв'язання: Розділяємо доданки при dx, dy та виписуємо для функції z диференціали P,Q:

Знайдемо часткові похідні першого порядку функцій P(x,y), Q(x,y):
З рівності часткових похідних 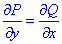 робимо висновок, що вираз dz є повним диференціалом.
робимо висновок, що вираз dz є повним диференціалом.
Функцію z знайдемо за допомогою криволінійного інтегралу 2-го роду: 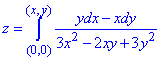
Наведений криволінійний інтеграл від точки (0,0) до точки (x,y) будемо обчислювати вздовж прямих x=0 і y=y0.
Так криволінійний інтеграл не залежить від контуру інтегрування, то криву інтегрування будемо будувати у вигляді ламаної з прямих, які паралельні осям і з'єднують крайні точки.
Це робиться з метою позбутися одного з диференціалів на кожному з проміжків інтегрування.
В цьому випадку ламану можна вибрати з наступних прямих
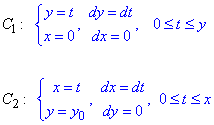
Тут також записано чому рівні відповідні диференціали.
Обчислимо криволінійний інтеграл 2 роду для відновлення функції z через повний диференціал:
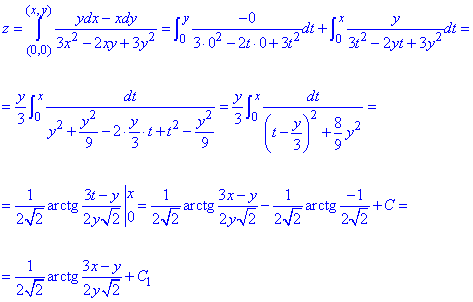
Уважно розберіть інтегрування.
Завдання 2 Знайти функцію z, якщо
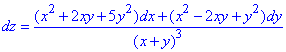
Розв'язання: Маємо диференціал:
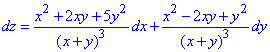
Тут позначимо
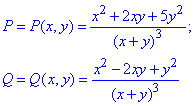
Знайдемо часткові похідні першого порядку функцій P(x,y) та Q(x,y):
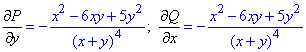
Як бачимо 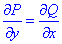 , тому вираз dz є повним диференціалом.
, тому вираз dz є повним диференціалом.
І функцію z знайдемо за допомогою криволінійного інтегралу 2-го роду:
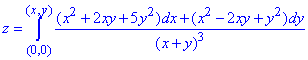
Отриманий криволінійний інтеграл від точки (1,0) до точки (x,y) будемо обчислювати вздовж прямих y=1 і x=x0.
Тобто
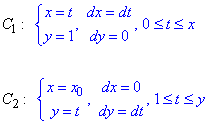
Відновимо функцію z за її повним диференціалом з допомогою криволінійного інтегралу другого роду
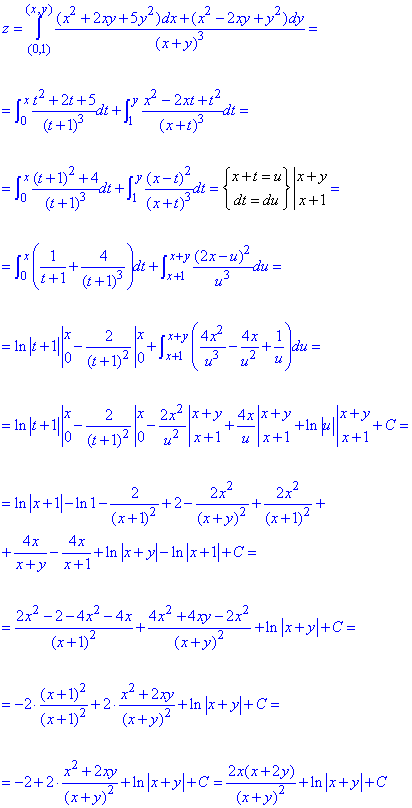
При інтегруванні виконали заміну змінних
Виписуємо кінцеве значення інтегралу рівне
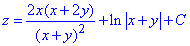
Попереду Вас чекають нові розв'язки на криволінійні, поверхневі, потрійні та інші інтеграли.


