Продовжуємо серію практичних уроків на знаходження криволінійних інтегралів І та ІІ роду. З цієї статті Ви навчитеся знаходити криволінійний інтеграл 2 роду.
У попередній статті дані основні формули, тому тут на них зупинятися не будемо і одразу переходимо до аналізу готових відповідей.
Після прочитання розв'язків Ви точно будете знати, як знайти криволінійний інтеграл ІІ роду.
Практика знаходження криволінійних інтегралів другого роду
ЗАВДАННЯ 2.6 Обчислити криволінійний інтеграл int((x2-2y)*dx+(y2-2xy)*dy,L) вздовж дуги L: y=x2 від точки A(-1;1) до точки B(1;1).
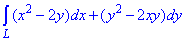
Розв'язання: За рівнянням функції y=x2 знаходимо її похідну dy=2x*dx, а з координат точок виписуємо проміжок інтегрування xє[-1;1].
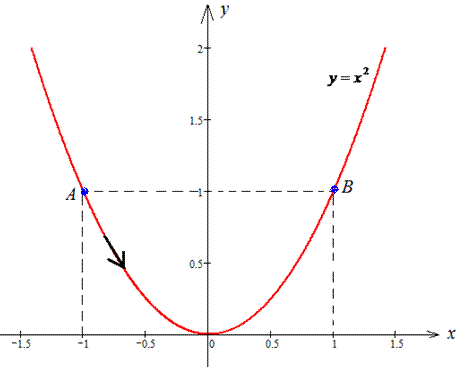
Необхідно обчислити криволінійний інтеграл ІІ роду, який спершу перетворюємо до визначеного інтегралу. Далі групуємо подібні доданки та знаходимо його значення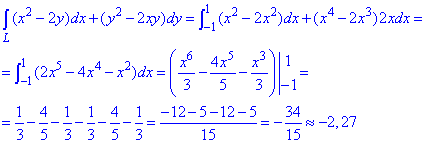
Такі інтеграли Ви повинні знаходити без помилок, вони найлегші з усіх тут наведених.
ЗАВДАННЯ 2.9 Обчислити криволінійний інтеграл int(y*dx+x/y*dy,L) вздовж дуги L: y=e-x від точки A(0;1) до точки B(-1;e).
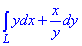
Розв'язання: Побудуємо дугу експоненту: y=e-x.
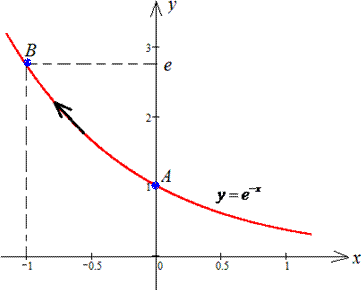
Виразимо диференціал dy=e-xdx та обмежимо проміжок [0;-1].
Переходимо до знаходження криволінійного інтегралу ІІ роду. 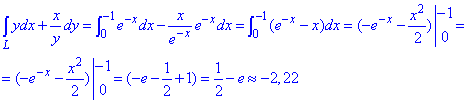
Експонента інтегрується без проблем, тому кому важко це вдається, аналізуйте формулу.
ЗАВДАННЯ 2.11 Обчислити криволінійний інтеграл int(x*cos(y)*dx-y*sin(x)*dy,L) вздовж дуги L: , де L - відрізок прямої від точки A(0;0) до точки B(3;6).
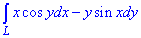
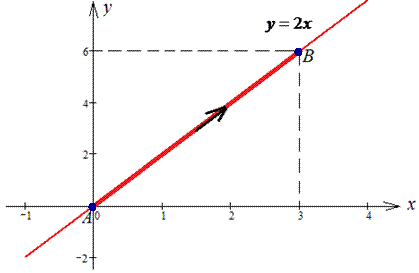
Розв'язання: Складемо рівняння прямої, що проходить через задані точки A(0;0) і B(3;6): 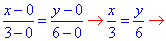
отримали y=2x, звідси dy=2dx . Аргумент змінюється від 1 до 3.
Для повного уявлення наводимо графік дуги
Криволінійний інтеграл ІІ роду зводимо до визначеного, який розкриваємо методом інтегрування частинами.
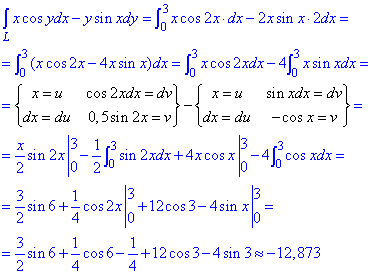
Так як з інтегруванням синусів і косинусів більшість студентів має труднощі, просимо проаналізувати формули. Це допоможе краще зрозуміти матеріал та легко виконати завдання на контрольній чи індивідуальній роботі.
ЗАВДАННЯ 2.13 Обчислити криволінійний інтеграл int((x+y)*dx-x*dy,L) вздовж дуги L: , де L: y=x2- відрізок прямої від точки A(-1;1) до B(1;1).

Розв'язання: Маємо y=x2, звідси dy=2dx. Графік дуги зображено нижче

Перетворюємо криволінійний інтеграл ІІ роду та обчислюємо значення. 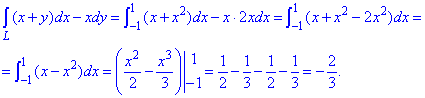
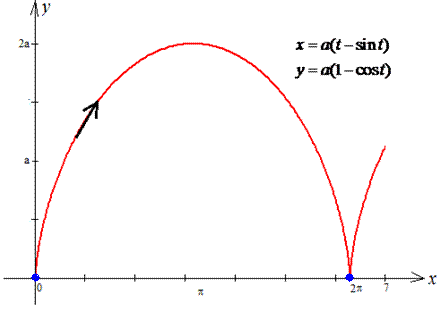
ЗАВДАННЯ 2.19 Обчислити криволінійний інтеграл int((2a-y)*dx-(a-y)*dy,L) вздовж дуги L: перша арка циклоїди x=a(t-sin(t)), y=a(1-cos(t)).
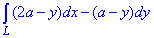
Розв'язання: Перша арка циклоїди знаходиться в межах tє[0;2Pi].
Похідні за параметром приймають значення dx=a*(1-cos(t))dt, dy=a*sin(t)dt.
Графік циклоїди в декартових координатах має вигляд
Криволінійний інтеграл ІІ роду за формулою рівний. 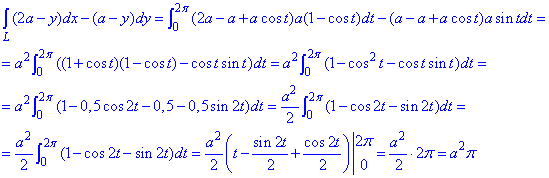
Тут понижували степінь косинуса за відомою тригонометричною формулою.
ЗАВДАННЯ 2.20 Обчислити криволінійний інтеграл int(y/(2x)*dx-x*dy,L) вздовж дуги L: y=ln(x) від точки A(1;0) до точки B(e2;2).
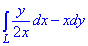
Розв'язання: Маємо логарифмічну функцію y=ln(x), звідси dy=dx/x . За умовою межі інтегрування рівні xє[0;e2]. Графік логарифма з точками A, B наведено нижче
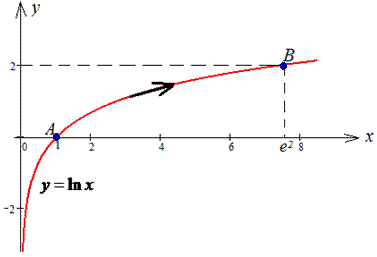
Як і у попередньому прикладі, перетворюємо криволінійний інтеграл ІІ роду до визначеного та обчислюємо його значення.
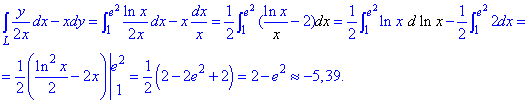
При цьому виконали досить поширений прийом, щоб внести логарифм під диференціал.
ЗАВДАННЯ 2.22 Обчислити криволінійний інтеграл int(sin(y)*dx+sin(x)*dy,L) вздовж дуги L: , де L - відрізок прямої від точки A(0;Pi) до точки B(Pi;0).
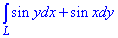
Розв'язання: Будуємо рівняння прямої, що проходить через задані точки A(0;Pi) і B(Pi;0): 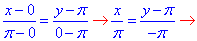
отримали y=-x+Pi. Для наочності наведемо вигляд прямої
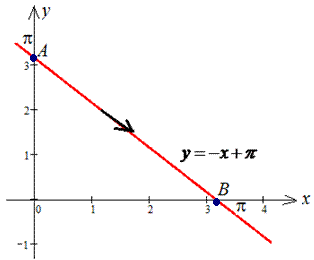
За рівнянням визначаємо диференціал дуги dy=-dx, а за координатами точок A(0;Pi), B(Pi;0) проміжок інтегрування [0;Pi].
За відомими формулами переходимо від криволінійного інтегралу ІІ роду до визначеного та знаходимо його
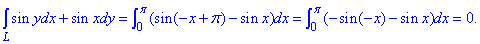
В результаті обчислень отримали нуль.
Як можна переконатися із схеми обчислень криволінійні інтеграли 2 роду досить легко знаходити.
Шукайте більше завдань на цю тему в наступних публікаціях.


