Розберемо розв'язки прикладів на обчислення криволінійних інтегралів другого роду вздовж просторових кривих.
Алгоритм обчислень Вам швидше запам'ятається з аналізу готових відповідей, основні переходи добре закоментовані та пояснені.
Завдання 1 Обчислити криволінійний інтеграл 2-го роду вздовж просторової кривої: int[(y-z)dx+(z-x)dy+(x-y)dz, C]
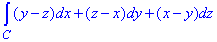
де C - коло x2+y2+z2=a2, y=x•tg(a) (0< alpha< π), що пробігається проти ходу годинникової стрілки, якщо дивитись з боку додатної частини осі Ox.
Розв'язання: Перше, що потрібно зробити це максимально спростити рівняння просторової дуги та знайти, якщо можливо криву перетину рівнянь.
Для цього підставимо y=x•tg(a) в рівняння сфери
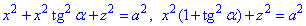
та зведемо отримане рівняння коло
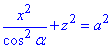
до параметричного вигляду.
Для цього виконаємо наступні перетворення координат
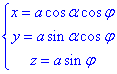
y таке, тому що
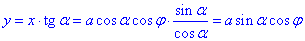
Межі зміни параметра φ все коло, тому кут пробігає значення 0≤φ ≤2π.
Далі в інтегралі потрібно замінити диференціали на такі, що залежні від кута φ .
Для цього знайдемо диференціали по змінній φ від функцій x=x(φ), y=y(φ), z=z(φ):

До цього все більш менш зрозуміло та всі розрахунки Ви можете повторити.
Кінцевим і найважчим етапом є обчислення криволінійного інтегралу 2-го роду вздовж просторової кривої:
під інтегралом x, y, z замінюємо на параметричні функції від кута φ, підставляємо знайдені диференціали, спрощуємо підінтегральну функцію та інтегруємо
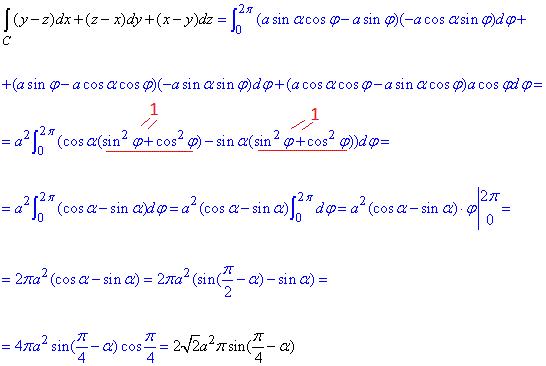
На словах це звучить досить просто, а от формула вже може більше розказати, що Вас чекає.
Та це ще не найскладніше, що Вас може чекати, родзинки ще попереду.
Завдання 2 Обчислити криволінійний інтеграл 2-го роду вздовж просторової кривої: int[ydx+zdy+xdz, C]
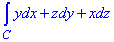
де C - частина гвинтової лінії x=a•cos(t), y=a•sin(t), z=b•t, що пробігається у напрямку зростання параметра 0≤t≤2π.
Розв'язання: Тут зразу маємо параметризоване рівняння просторової кривої, яке вже немає куди далі спрощувати.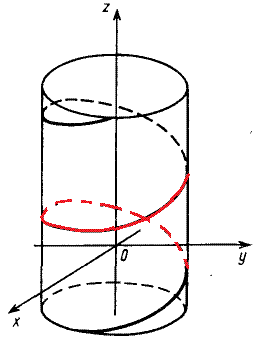
Тому переходимо до обчислення диференціалів по змінній t від функцій x=x(t), y=y(t), z=z(t):
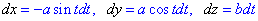
Підставляємо та обчислюємо криволінійний інтеграл 2-го роду вздовж гвинтової лінії:
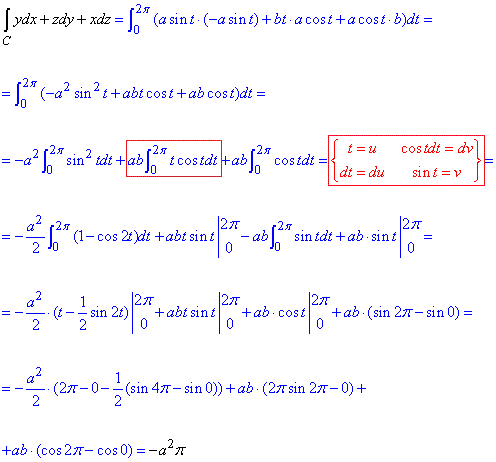
При обчисленні застосували інтегрування частинами.
І наостанок, розв'яжемо складний криволінійний інтеграл 2 порядку вздовж кривої Вівіані.
Завдання 3 Обчислити криволінійний інтеграл 2-го роду вздовж просторової кривої: int[y2dx+z2dy+x2dz, C]
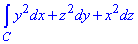
де C - частина кривої Вівіані x2+y2+z2=a2, x2+y2=ax (z≥0, a>0), що пробігається проти ходу годинникової стрілки, якщо дивитись з боку додатної частини (x>a) осі Ox.
Розв'язання: Зведемо задане коло до параметричного вигляду за допомогою формул переходу до полярної системи координат:
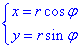
тоді рівняння x2+y2=ax матиме простий вигляд
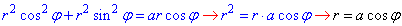
Рівняння сфери x2+y2+z2=a2 перетворимо підстановкою полярних координат:
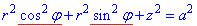
звідси r2+z2=a2, далі підставляємо r=a•cos(φ) і виражаємо третю координату z як функцію кута:
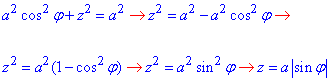 ,
,
В підсумку отримали параметризовану криву:
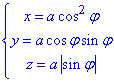
де –π/2≤φ≤π/2.
Запишемо диференціали по змінній φ від функцій x=x(φ), y=y(φ), z=z(φ):
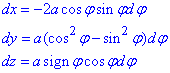
А далі наберіть побільше повітря і дочитайте обчислення криволінійного інтегралу 2-го роду до кінця:
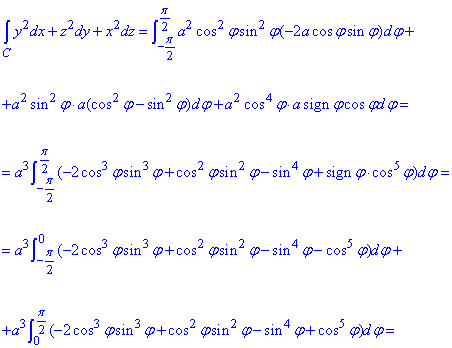
Тут зробимо заміну змінних:
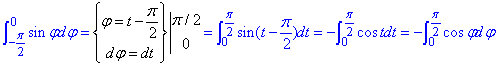
продовжуємо інтегрування
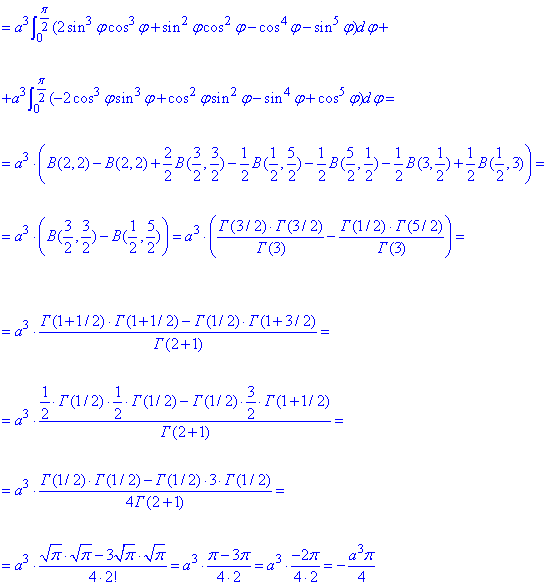
Не лякайтеся наведених Бета та Гамма функцій, до такого в Вашій практиці навряд чи дійде, але якщо Ви маєте бажання пов'язати майбутнє з математикою то обов'язково маєте познайомитися з наступними функціями.
В цьому завданні були використані Ейлерові інтеграли (гама і бета функції):
Гама-функція Ейлера:
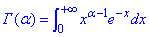
Деякі властивості гама-функції (зокрема, які використано в цьому прикладі):
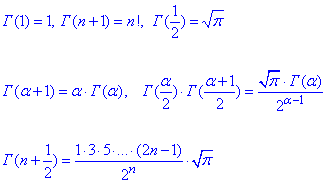
Тут n- натуральне число.
Бета-функція Ейлера:
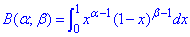
Деякі властивості бета-функції:
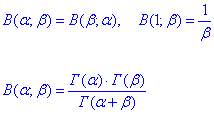
З наведених прикладів Ви повинні запам'ятати методику обчислення криволінійних інтегралів вздовж просторових кривих.
У Вас будуть зовсім інші криві, як і підінтегральні функції, тому наведена стаття буде слугувати лиш доброю інструкцією, все решта залежатиме від Ваших умінь інтегрувати.
Тому інтегруйте самостійно та розв'язуйте побільше подібних завдань!


