Задачі з дослідження векторного поля, що включають знаходження циркуляції, потоку розглянуті на попередніх уроках. Тут ми покажемо, як швидко перевірити, а якщо й потрібно то і довести, що поле є потенціальним та соленоїдальним. Умови за яких це виконується детально розписані в поясненнях до обчислень.
Детальний аналіз кожного з прикладів дозволяє самостійно освоїти дану тему кожному студентові.
ЗАВДАННЯ 10.4 Перевірити чи буде векторне поле F=(5x+4yz)*i+(5y+4xz)*j+(5z+4xy)*k
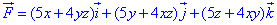потенціальним і соленоїдним. Якщо поле
потенціальне, то знайти його потенціал.
Розв'язання: Для того, щоб задане поле було потенціальним, необхідно і достатньо, щоб ротор векторного поля був рівний нулю rot(F)=0.
За умовою виписуємо функції, які необхідні для подальших розрахунків
P=P(x;y;z)=5x+4yz, Q=Q(x;y;z)=5y+4zx, R=R(x;y;z)=5z+4xy.
Звідси ротор векторного поля через часткові похідні знаходимо за формулою
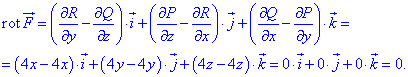З обчислень бачимо, що векторне поле є потенціальним.
Знайдемо потенціал u=u(x;y;z) заданого векторного поля .
Згідно з теорією векторне поле рівне градієнту потенціалу:
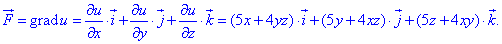Випишемо компоненти градієнту з початкової умови F=(5x+4yz)*i+(5y+4xz)*j+(5z+4xy)*k
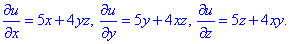
Далі інтегруванням відновлюємо потенціал, спершу інтегруємо похідну по x, далі знайдений потенціал диференціюємо по y та прирівнюємо до 2 часткової похідної, і т.д.
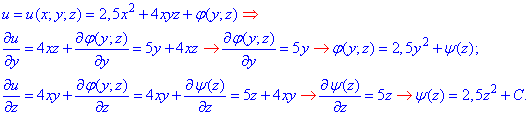Тут не писали знак інтегрування, оскільки маємо справу з простими табличними інтегралами, а такий запис економить час, зберігаючи при цьому суть операцій.
Остаточно записуємо потенціал u векторного поля :
u(x;y;z)=2,5(x2+y2+z2)+4xyz+C, де C - довільна константа.
Для того, щоб векторне поле було соленоїдним, необхідно і достатньо, щоб його дивергенція була рівна нулю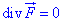 
Перевіряємо цю умову:
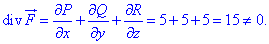Вона не виконується, отже розглянуте векторне поле не є соленоїдним.
ЗАВДАННЯ 10.5 Перевірити, чи буде векторне поле F=(x+2yz)*i+(y+2xz)*j+(z+2xy)*k
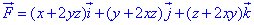потенціальним і соленоїдним. Якщо поле потенціальне, то знайти його потенціал.
Розв'язання: Необхідною і достатньою умовою, що векторне поле - потенціальне є рівність нулю ротора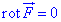 
.
З початкової умови записуємо P=P(x;y;z)=x+2yz, Q=Q(x;y;z)=y+2xz, R=R(x;y;z)=z+2xy.
За формулою знаходимо ротор векторного поля
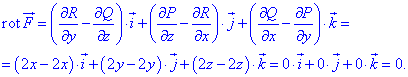Робимо висновок про те, що поле є потенціальним.
Знайдемо потенціал u(x,y,z).
Градієнт рівний:
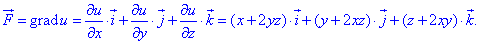Виписуємо часткові похідні
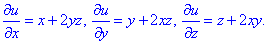
а далі інтегруванням відновлюємо функцію
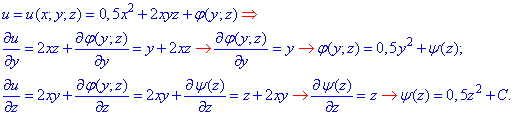Потенціалу векторного поля приймає значення
u(x;y;z)=0,5(x2+y2+z2)+2xyz+C,
де C - довільна константа.
Умова що векторне поле соленоїдальне рівносильна рівності нулю його дивергенції 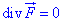. Виконуємо необхідні розрахунки
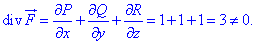
З запису бачимо, що умова не виконується, отже задане векторне поле не є соленоїдним.
ЗАВДАННЯ 10.6 Перевірити, чи буде векторне поле F=(4x-7yz)*i+(4y-7xz)*j+(4z-7xy)*k
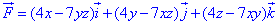потенціальним і соленоїдним. Якщо поле потенціальне, то знайти його потенціал.
Розв'язання: Поле F є потенціальним, якщо його ротор рівний нулю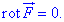 
За умовою виписуємо складові P=P(x;y;z)=4x-7yz, Q=Q(x;y;z)=4y+7xz, R=R(x;y;z)=4z-7xy
та підставляємо у формулу ротора
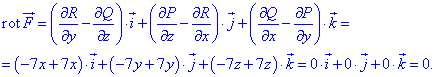Отримали в результаті нуль, можемо зробити висновок, що векторне поле є потенціальним.
Потенціал u=u(x;y;z) векторного поля знаходимо через формулу градієнта:
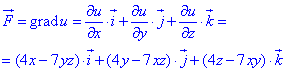Часткові похідні, згідно початкової умови, мають наступні значення
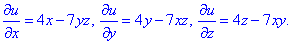
Повторно інтегруючи їх визначаємо функцію u(x;y;z)
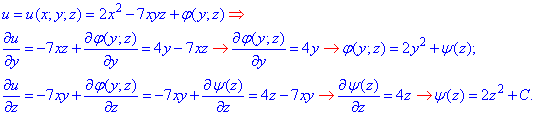Уважно перегляньте та розберіть, в чому суть наведених вище формул. Інтегруванням за змінною 'х' ми отримуємо потенціал + функцію від двох інших координат phi(y,z). Знайшовши часткову похідну потенціалу за змінною 'y' і, прирівнявши до часткової похідної з векторного поля, довизначаємо функцію phi(y,z), одна залишається невідома psi(z). Для її визначення знаходимо часткову похідну потенціалу за 'z' та прирівнянням до третьої компоненти векторного поля, отримуємо її часткову похідну. Далі через інтеграл її довизначаємо. Вкінці залишається підставити всі знайдені функції в початковий запис.
Таким чином, потенціал поля рівний
u(x;y;z)=2(x2+y2+z2)-7xyz+C, де C - довільна константа.
Перевірка заданого поля на соленоїдальність рівносильна знаходженню дивергенції і перевірці чи вона рівна нулю.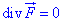
Самі обчислення не складні, варто лише знати або мати під рукою формулу дивергенції
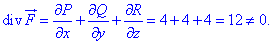
Бачимо, що дане поле не є соленоїдним.
ЗАВДАННЯ 10.7 Перевірити, чи буде векторне поле F=(12x+yz)*i+(12y+xz)*j+(12z+xy)*k
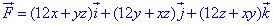потенціальним і соленоїдним. Якщо поле 
потенціальне, то знайти його потенціал.
Розв'язання: Перевіряємо чи ротор векторного поля рівний нулю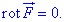 
Маємо функції P=P(x;y;z)=12x+yz, Q=Q(x;y;z)=12y+xz, R=R(x;y;z)=12z+xy
які підставляємо у формулу
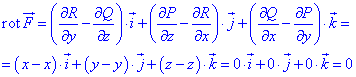Умова рівності нулю ротора виконується, отже векторне поле є потенціальним.
Відшукаємо потенціал u(x;y;z).
Для цього застосовуємо форму запису векторного поля через градієнт потенціалу:
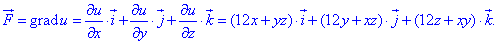Таким чином отримаємо часткові похідні
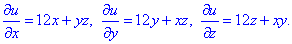
Методика знаходження потенціалу векторного поля детально розписана в попередніх задачах.
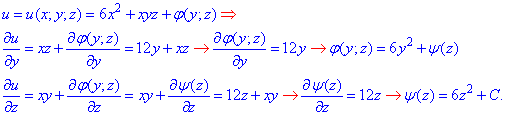Слід зазначити, що за перше наближення можна брати будь-яку з трьох часткових похідних. Вибирати порядок Вам, кінцевий інтеграл від цього не зміниться.
Формула потенціалу векторного поля прийме вигляд:
u(x;y;z)=6(x2+y2+z2)+xyz+C , де C - довільна константа.
Перевіримо чи векторне поле буде соленоїдним.
Для цього повинна виконуватися умова div(F)=0:
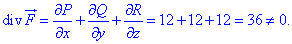З розрахунків бачимо, що дивергенція відмінна від нуля, отже робимо висновок що поле не є соленоїдним.
ЗАВДАННЯ 10.10 Перевірити, чи буде векторне поле F=(6x+7yz)*i+(6y+7xz)*j+(6z+7xy)*k
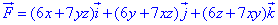потенціальним і соленоїдним. Якщо поле потенціальне, то знайти його потенціал.
Розв'язання: З попередніх прикладів Ви вже можливо запам'ятали що спершу потрібно знайти ротор векторного поля.
Виписуємо функції
P=P(x;y;z)=6x+7yz, Q=Q(x;y;z)=6y+7xz, R=R(x;y;z)=6z+7xy
та за формулою знаходимо ротор
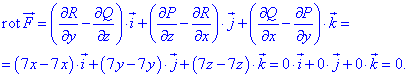Він рівний нулю, а це значить, що досліджуване векторне поле є потенціальним.
Для відшукання потенціалу u(x;y;z) скористаємося схемою, яка детально повторюється з прикладу в приклад.
Виписуємо рівняння градієнту потенціалу:
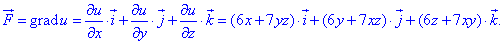з нього маємо часткові похідні
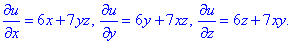
які використовуємо при інтегруванні та довизначенні u(x;y;z)
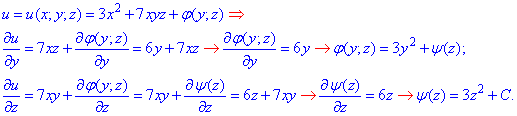Після всіх розрахунків потенціал векторного поля матиме запис:
u(x;y;z)= 3(x2+y2+z2)+7xyz+C, де C - довільна константа.
Залишилося перевірити чи поле є соленоїдним.
Для цього маємо умову :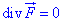
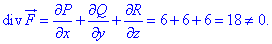
Обчислення показали, що умова рівності нулю дивергенції не виконується. Значить векторне поле не є соленоїдним.
ЗАВДАННЯ 10.12 Перевірити, чи буде векторне поле F=(3x+yz)*i+(3y+xz)*j+(3z+xy)*k
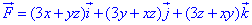потенціальним і соленоїдним. Якщо поле потенціальне, то знайти його потенціал.
Розв'язання: Ви вже мали б знати для того, щоб задане векторне поле було потенціальним, необхідно і достатньо, щоб ротор був рівний нулю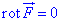
.
Виписуємо функції P=P(x;y;z)=3x+yz, Q=Q(x;y;z)=3y+xz, R=R(x;y;z)=3z+xy.
та за наведеною нижче формулою знаходимо ротор
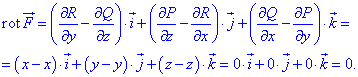Він рівний нулю, тому задане векторне поле є потенціальним.
Знайдемо його потенціал u(x;y;z).
Формула градієнту потенціалу має вигляд:
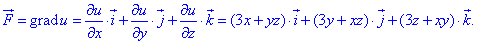З неї виписуємо часткові похідні
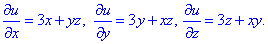
а далі через неозначені інтеграли знаходимо потенціал
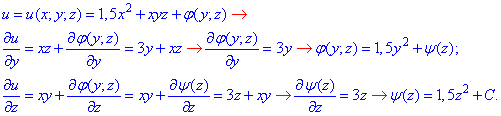Як вже зазначалося вище, в наведених формулах для зменшення громіздкості опущено знаки інтегрування. В обчисленнях це допустимо, проте, якщо викладачі від Вас вимагають детального опису всіх проміжних викладок, не забувайте, що тут ми маємо на увазі невизначені інтеграли.
Остаточно записуємо явний вигляд потенціалу поля
u(x;y;z)= 1,5(x2+y2+z2)+xyz+C , тут C - будь-яка константа.
І остання перевірка на умову, що задане векторне поле було соленоїдним (div(F)=0)
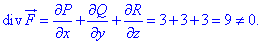показує, що задане поле не є соленоїдним (дивергенція відмінна від нуля).
ЗАВДАННЯ 10.21 Довести, що векторне поле F=yz*i+xz*j+xy*k
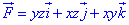є потенціальним і соленоїдним.
Розв'язання: Умова відповідності векторного поля потенціальному має вигляд
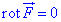
Виписуємо функції P=P(x;y;z)=yz, Q=Q(x;y;z)=xz, R=R(x;y;z)=xy
та підставяємо в рівняння ротора
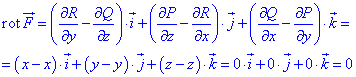
Маємо рівність нулю, таким чином перевірили і довели, що задане векторне поле є потенціальним.
Щоб знайти потенціал u(x;y;z) векторного поля використовуємо градієнт:
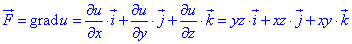З вхідних даних завдання виписуємо часткові похідні u(x;y;z)
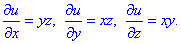
Далі інтегруванням поступово знаходимо u(x;y;z)
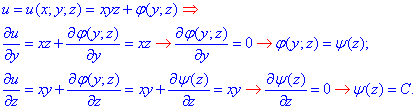
Формула потенціалу векторного поля набуде вигляду:
u(x;y;z)= xyz+C , де C - будь-яка стала.
Залишилося довести, що векторне поле є соленоїдним.
Для цього знаходимо дивергенцію
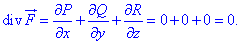і переконуємося, що вона рівна нулю.
Це означає, що векторне поле є соленоїдним, що і слід було доказати.
ЗАВДАННЯ 10.23 Перевірити, чи буде векторне поле F=(x2+yz)*i+(y2+xz)*j+(z2+4xy)*k
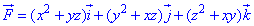потенціальним і соленоїдним. Якщо поле потенціальне, то знайти його потенціал.
Розв'язання: Перевірка умови рівності нулю ротора векторного поля однозначно дозволяє з'ясувати чи векторне поле є потенціальним, чи ні.
З початкової умови виписуємо
P=P(x;y;z)=x2+yz, Q=Q(x;y;z)=y2+xz, R=R(x;y;z)=z2+xy
та застосовуємо формулу ротора
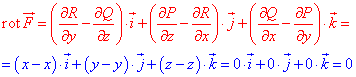
Умова виконується, тому робимо висновок що векторне поле є потенціальним.
Як знайти потенціал u(x;y;z) детально описано в методиці і поясненнях до розрахунків. Але знову і знову проходимося по пунктах, оскільки, як показує практика студенти живуть за правилом "вивчив - здав -забув".
Нам потрібно записати градієнт поля через часткові похідні:
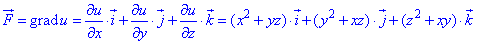Далі їх виписуємо
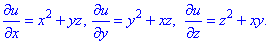
Потім почергово інтегруючи їх та диференціюючи знайдені потенціали, знаходимо явний вигляд u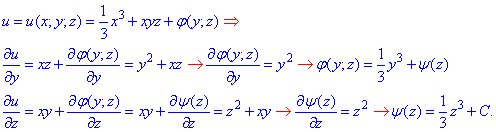
В результаті отримаємо наступне рівняння потенціалу
u(x;y;z)= 1/3*(x3+y3+z3)+xyz+C
Перевірка поля на виконання умови div(F)=0 дозволяє встановити, чи є векторне поле соленоїдним.
Виконуємо обчислення:
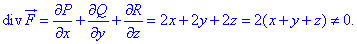Робимо висновок, що задане векторне поле не є соленоїдним.
З розглянутих прикладів Ви могли зауважити, що не кожне потенціальне поле є соленоїдним.
Формул для перевірки умов не так багато і вони детально розписані. Вважаємо, що наведений матеріал в повній мірі дозволяє Вам виконати самостійно розрахунки аналогічних прикладів.
