Задачи по исследованию векторного поля, что включают нахождение циркуляции, потока рассмотрены на предыдущих уроках. Здесь мы покажем, как быстро проверить, а если и нужно то и доказать, что поле является потенциальным и соленоидальным. Условия за которых это выполняется детально расписанны в объяснениях к вычислениям.
Детальный анализ каждого из примеров позволяет самостоятельно освоить данную тему каждому студенту.
ЗАДАНИЕ 10.4 Проверить, является ли векторное поле F=(5x+4yz) *i+(5y+4xz)*j+(5z+4xy)*k
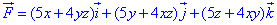потенциальным и соленоидным.
Если поле 
потенциальное, то найти его потенциал.
Решение: Для того, чтобы заданое поле было потенциальным, необходимо и достаточно, чтобы ротор векторного поля был равен нулю rot(F)=0.
За условием выписываем функции, которые необходимы для дальнейших расчетов
P=P(x;y;z)=5x+4yz, Q=Q(x;y;z)=5y+4zx, R=R(x;y;z)=5z+4xy.
Отсюда ротор векторного поля через частичные производные находим по формуле
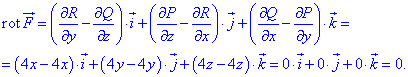Из вычислений видим что векторное поле является потенциальным.
Найдем потенциал u=u(x;y;z) заданного векторного поля .
Согласно теории, векторное поле равно градиенту потенциала:
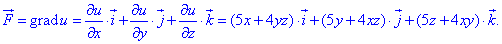Выпишем компоненты градиента из начального условия F= (5x+4yz) *i+ (5y+4xz) *j+ (5z+4xy) *k 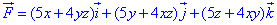потенциальным и соленоидным. Если полетпотенциальное, то найти его потенциал.
Решение: Для того, чтобы задано поле было потенциальным, необходимо и достаточно, чтобы ротор векторного поля был равен нулю rot (F) =0.
За условием выписываем функции, которые необходимы для дальнейших расчетов
P=P (x;y;z) =5x+4yz, Q=Q (x;y;z) =5y+4zx, R=R (x;y;z) =5z+4xy.
Отсюда ротор векторного поля через частичные производные находим за формулой
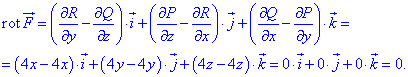Из вычислений видим, что векторное поле является потенциальным.
Найдем потенциал u=u (x;y;z) заданного векторного поля .
Согласно теории векторное поле равно градиенту потенциала :
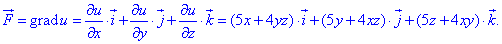Выпишем компоненты градиенту из начального условия F=(5x+4yz)*i+(5y+4xz)*j+(5z+4xy)*k
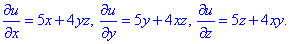
Дальше интегрированием возобновляем потенциал, сначала интегрируем производную по x, потом найденный потенциал дифференцируем по y и приравниваем ко 2 частичной производной, и так далее
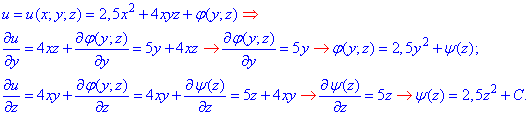Здесь не ставили знак интегрирования, поскольку имеем дело с простыми табличными интегралами, а такая запись экономит время, храня при этом суть операций.
Окончательно записываем потенциал u векторного поля :
u(x;y;z)=2,5(x2+y2+z2)+4xyz+C, где C - произвольная константа.
Чтобы векторное поле было соленоидным, необходимо и достаточно, чтобы его дивергенция была равна нулю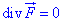 
Проверяем это условие:
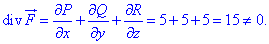Она не выполняется, следовательно рассмотреное векторное поле не является соленоидным.
ЗАДАНИЕ 10.5 Проверить будет ли векторное поле F=(x+2yz) *i+(y+2xz)*j+(z+2xy)*k
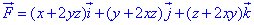потенциальным и соленоидным.
Если поле потенциальное, то найти его потенциал.
Решение: Необходимым и достаточным условием, что векторное поле - потенциальное является равенство нулю ротора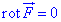 
Из начального условия записываем P=P(x;y;z)=x+2yz, Q=Q(x;y;z)=y+2xz, R=R(x;y;z)=z+2xy.
По формуле находим ротор векторного поля
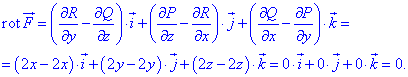Делаем вывод о том, что полет является потенциальным.
Найдем потенциал u(x, y, z).
Градиент равен:
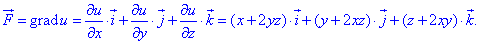Выписываем частичные производные
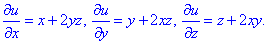
а дальше интегрированием возобновляем функцию
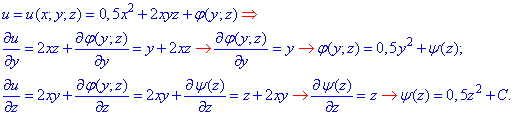
Потенциал векторного поля принимает значение
u (x;y;z)=0,5(x2+y2+z2) +2xyz+C,
где C - произвольная константа.
Условие что векторное поле соленоидальное равносильная равенству нулю его дивергенции
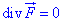
Выполняем необходимые расчеты
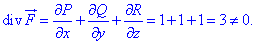
Из записи видим, что условие не выполняется, следовательно векторное поле не является соленоидным.
ЗАДАНИЕ 10.6 Проверить, является ли векторное поле F=(4x-7yz)*i+(4y-7xz)*j+(4z-7xy)*k
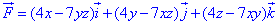потенциальным и соленоидным.
Если полет потенциальное, то найти его потенциал.
Решение: Полет F является потенциальным, если его ротор равен нулю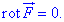 
За условием выписываем составляющие P=P(x;y;z)=4x-7yz, Q=Q(x;y;z)=4y+7xz, R=R(x;y;z)=4z-7xy
и подставляем в формулу ротора
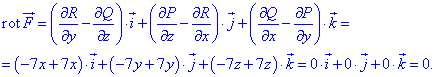Получили в результате нуль, можем сделать вывод, что векторное поле является потенциальным.
Потенциал u=u(x;y;z) векторного поля находим через формулу градиента :
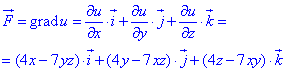Частичные производные, согласно начальному условию, имеют следующие значение
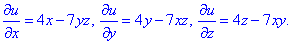
Повторно интегрируя их определяем функцию u(x;y;z)
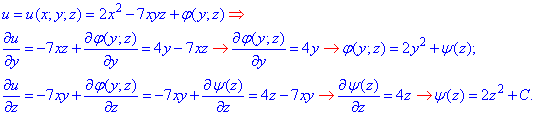Внимательно пересмотрите и разберите, в чем суть вышеприведенных формул.
Интегрированием за переменной 'х' мы получаем потенциал + функцию от двух других координат phi(y,z).
Найдя частичную производную потенциала за переменной 'y' и, приравняв к частичной производной из векторного поля, доопределяем функцию phi(y,z), остается одна неизвестная psi(z).
Для ее определения находим частичную производную потенциала по 'z' приравниванием к третьей компоненте векторного поля, получаем ее частичную производную.
Далее через интеграл ее доопределяем. Напоследок остается подставить все найденные функции в начальную запись.
Таким образом, потенциал поля равен
u(x;y;z)=2(x2+y2+z2)-7xyz+C, где C - произвольная константа.
Проверка поля F на соленоидальность равносильня нахождению дивергенции и проверке равна ли она нулю.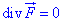
Сами вычисления не сложны, стоит лишь знать или иметь под рукой формулу дивергенции
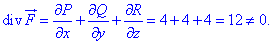
Видим, что поле не является соленоидным.
ЗАДАНИЕ 10.7 Проверить, или будет векторное поле F=(12x+yz)*i+(12y+xz)*j+(12z+xy)*k
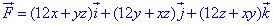потенциальным и соленоидным.
Если поле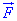 
потенциальное, то найти его потенциал.
Решение: Проверяем равен ли ротор векторного поля нулю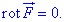 
Имеем функции P=P(x;y;z)=12x+yz, Q=Q(x;y;z)=12y+xz, R=R(x;y;z)=12z+xy
которые подставляем в формулу
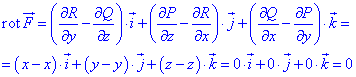Условие равенства нулю ротора выполняется, следовательно векторное поле является потенциальным.
Отыщем потенциал u(x;y;z).
Для этого применяем форму записи векторного поля через градиент потенциала:
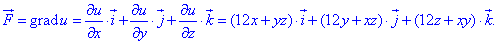Таким образом получим частичные производные
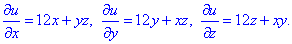
Методика нахождения потенциала векторного поля детально расписана в предыдущих задачах.
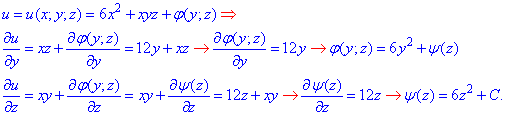Следует отметить, что за первое приближение можно брать любую из трех частичных производных.
Выбирать порядок Вам, конечный интеграл от этого не изменится.
Формула потенциала векторного поля примет вид:
u(x;y;z)=6(x2+y2+z2)+xyz+C, где C - произвольная сталая.
Проверим, является ли векторное поле соленоидным.
Для этого должно выполняться условие div(F)=0:
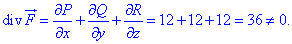Из расчетов видим, что дивергенция не равна нуля, следовательно делаем вывод что поле не является соленоидным.
ЗАДАНИЕ 10.10 Проверить, является ли векторное поле F=(6x+7yz)*i+(6y+7xz)*j+(6z+7xy)*k
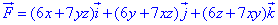потенциальным и соленоидным.
Если поле потенциальное, то найти его потенциал.
Решение: Из предыдущих примеров Вы уже возможно запомнили что сначала нужно найти ротор векторного поля.
Выписываем функции
P=P(x;y;z)=6x+7yz, Q=Q(x;y;z)=6y+7xz, R=R(x;y;z)=6z+7xy
и по формуле находим ротор
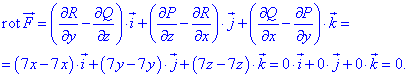Он равен нулю, а это значит, что исследуемое векторное поле является потенциальным.
Для возобновления потенциала u(x;y;z) воспользуемся схемой, которая детально повторяется из примера в пример.
Выписываем уравнение градиента потенциала:
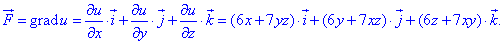из него имеем частичные производные
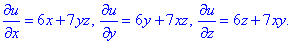
какие используем при интегрировании и доопределении u(x;y;z)
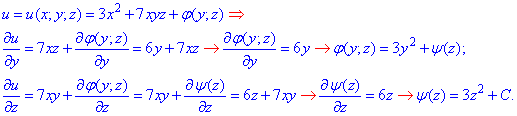После всех расчетов потенциал векторного поля будет равен:
u(x;y;z)=3(x2+y2+z2)+7xyz+C, где C - произвольная константа.
Осталось проверить, является ли поле F соленоидным.
Для этого имеем условие :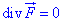
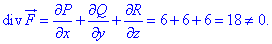
Вычисления показали, что условие равенства нулю дивергенции не выполняется.
Следовательно, векторное поле не является соленоидным.
ЗАДАНИЕ 10.12 Проверить, будет ли векторное поле F=(3x+yz)*i+(3y+xz)*j+(3z+xy)*k
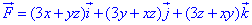потенциальным и соленоидным.
Если поле потенциальное, то найти его потенциал.
Решение: Вы уже должны были бы знать, чтобы векторное поле было потенциальным, необходимо и достаточно, чтобы ротор rot(F) был равен нулю.
Выписываем функции P=P(x;y;z)=3x+yz, Q=Q(x;y;z)=3y+xz, R=R(x;y;z)=3z+xy.
и за нижеприведенной формулой находим ротор
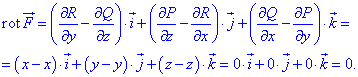Он равен нулю, поєтому векторное поле F является потенциальным.
Найдем потенциал u(x;y;z).
Формула градиента потенциала имеет вид:
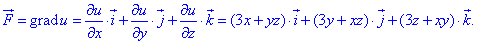Из нее выписываем частные производные
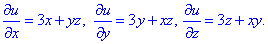
а дальше через неопределенные интегралы находим потенциал
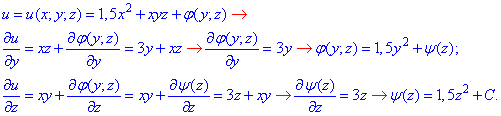Как уже отмечалось выше, в приведенных формулах для уменьшения громоздкости опущены знаки интегрирования.
В вычислениях это допустимо, однако, если преподаватели от Вас требуют детального расписания всех промежуточных объяснений, не забывайте, что здесь мы имеем в виду неопределенные интегралы.
Окончательно записываем явный вид потенциала поля
u (x;y;z)=1,5(x2+y2+z2)+xyz+C, здесь C - любая константа.
И последняя проверка на условия, что векторное поле является соленоидным (div (F) =0)
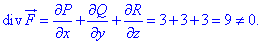Видим что поле F не является соленоидным (дивергенция отличается от нуля).
ЗАДАНИЕ 10.21 Доказать, что векторное поле F=yz*i+xz*j+xy*k
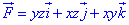является потенциальным и соленоидным.
Решение: Условие соответствия векторного поля F потенциальному имеет вид
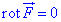
Выписываем функции P=P(x;y;z)=yz, Q=Q(x;y;z)=xz, R=R(x;y;z)=xy
и ичитываем в уравнении ротора
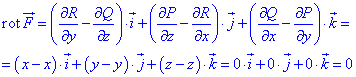
Имеем равенство нулю ротора, таким образом проверили и доказали, что векторное поле F является потенциальным.
Чтобы найти потенциал u(x;y;z) векторного поля используем градиент:
Из входных данных задания выписываем частичные производные u(x;y;z)
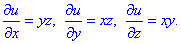
Дальше интегрированиям постепенно возобновляем u(x;y;z)
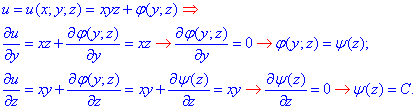
Формула потенциала векторного поля приобретет вид:
u (x;y;z)=xyz+C, где C - любая сталая.
Осталось доказать, что векторное поле является соленоидным.
Для этого находим дивергенцию
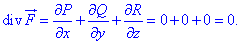и убеждаемся, что она равна нулю.
Это значит, что векторное поле является соленоидным, что и следовало досказать.
ЗАДАНИЕ 10.23 Проверить, является ли векторное поле F=(x2+yz)*i+(y2+xz)*j+(z2+4xy)*k
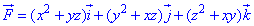потенциальным и соленоидным.
Если поле потенциальное, то найти его потенциал.
Решение: Проверка условия равенства нулю ротора векторного поля однозначно позволяет выяснить, является ли векторное поле потенциальным, или нет.
Из начального условия выписываем
P=P(x;y;z)=x2+yz, Q=Q(x;y;z)=y2+xz, R=R(x;y;z)=z2+xy
и применяем формулу ротора
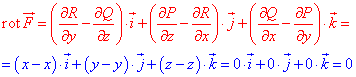
Условие выполняется, поэтому делаем вывод что векторное поле является потенциальным.
Как найти потенциал (x;y;z) детально описано в методике и объяснениях к расчетам.
Но снова и снова проходимся по пунктам, поскольку, как показывает практика студенты живут по правилу "выучил - сдал - забыл".
Нам нужно записать градиент поля через частные производные:
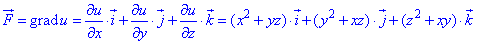Дальше их выписываем
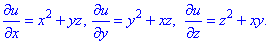
Потом поочередно интегрируя их и дифференцируя найденные потенциалы, находим явный вид u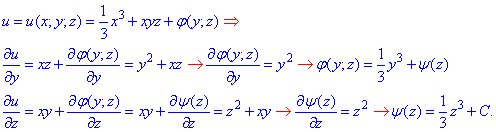
В результате получим следующее уравнение потенциала
u(x;y;z)=1/3*(x3+y3+z3)+xyz+C
Проверка поля на выполнение условия div(F)=0 позволяет установить, является ли векторное поле соленоидным.
Выполняем вычисления:
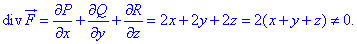Делаем вывод, что задано векторное поле F не является соленоидным.
Из рассмотренных примеров Вы могли заметить, что не каждое потенциальное поле является соленоидным.
Формул для проверки условий не так много и они детально расписаны. Считаем, что приведенный материал в полной мере позволяет Вам выполнить самостоятельно расчеты аналогичных примеров.
