В цій статті навчимося обчислювати криволінійний інтеграл від повного диференціалу.
Схема розв'язувань:
- спершу потрібно переконатися, що підінтегральна функція є повним диференціалом
- далі знайти інтеграл між заданими точками.
Формула Ньютона—Лейбніца для криволінійного інтеграла від повного диференціала
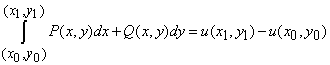
Криволінійний інтеграл має одну корисну для обчислень властивість, він не залежить від форми кривої, по якій інтегруємо. Тому замість інтегрувати по прямій між двома точками будують ламану паралельні осям координат і інтегрують по ній.
За рахунок цього один з диференціалів в інтегралі перетворюється в нуль, що спрощує обчислення.
Детальніше алгоритм перевірки підінтегрального виразу на повний диференціал та обчислення криволінійних інтегралів наведені в наступних 6 прикладах.
Завдання 1 Переконавшись, що підінтегральний вираз є повним диференціалом, обчислити криволінійний інтеграл int[(x+y)dx+(x-y)dy]
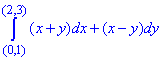
Розв'язання: Підінтегральні функції є первісними для повного диференціала
(x+y)dx+(x-y)dy.
Випишемо P=P(x,y)=x+y, Q=Q(x,y)=x-y
та знайдемо часткові похідні першого порядку функцій P(x,y) та Q(x,y):
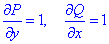
Порівнянням переконуємось, що часткові похідні рівні
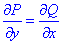
тому підінтегральний вираз (x+y)dx+(x-y)dy є повним диференціалом.
Криволінійний інтеграл від точки (0,1) до точки (2,3) будемо обчислювати вздовж прямих y=1 і x=2.
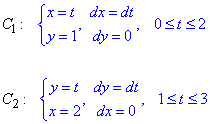
Так зручно виконувати оскільки на кожному інтервалі один з диференціалів рівний нулю, отже інтеграл спрощується.
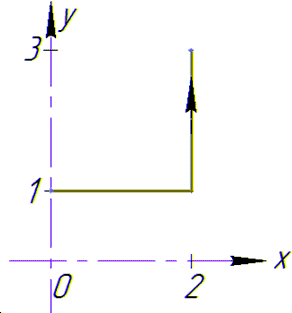
Обчислимо заданий криволінійний інтеграл:
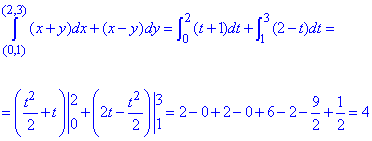
Завдання 2 Переконавшись, що підінтегральний вираз є повним диференціалом, обчислити криволінійний інтеграл
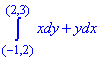
Розв'язання: Маємо підінтегральний вираз:
xdy+ydx.
Випишемо значення при диференціалах
P=P(x,y)=y, Q=Q(x,y)=x.
Знайдемо часткові похідні першого порядку функцій P,Q:
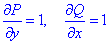
Порівнянням значень переконуємось, що підінтегральний вираз є повним диференціалом.
Заданий криволінійний інтеграл від точки (-1,2) до точки (2,3) будемо обчислювати вздовж прямих y=2 і x=2.
На графіку напрям та контур інтегрування мають вигляд
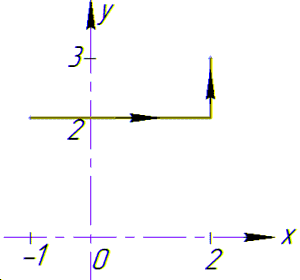
Випишемо як змінюватимусь координати та диференціали на кожному інтервалі
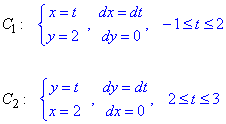
Знайдемо криволінійний інтеграл через суму двох:
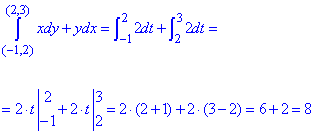
Завдання 3 Переконавшись, що підінтегральний вираз є повним диференціалом, обчислити криволінійний інтеграл
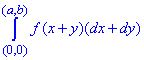
де f(u) неперервна.
Розв'язання: Виписуємо підінтегральний вираз:
f(x+y)(dx+dy)=f(x+y)dx+f(x+y)dy.
Звідси P=P(x,y)=f(x+y), Q=Q(x,y)=f(x+y).
Оскільки P, Q симетрично містять змінні, то їх часткові похідні
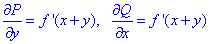
рівні, а значить підінтегральний вираз є повним диференціалом.
Криволінійний інтеграл від точки (0,0) до точки (a,b) будемо обчислювати вздовж прямих y=0 і x=a.
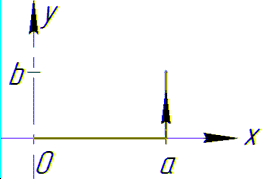
Випишемо межі інтегралу та диференціали
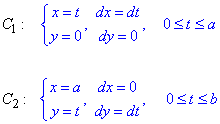
Криволінійний інтеграл спрощуємо за допомогою заміни змінних:
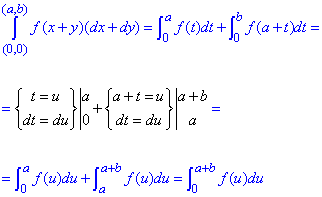
тут f(u) неперервна функція.
Завдання 4 Переконавшись, що підінтегральний вираз є повним диференціалом, обчислити криволінійний інтеграл
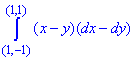
Розв'язання: Підінтегральний вираз
(x-y)dx-(x-y)dy.
Далі ф-ї P=P(x,y)=x-y; P=P(x,y)=-x+y.
Знайдемо часткові похідні від P, Q:
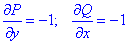
Мішані похідні рівні
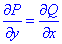
тому підінтегральний вираз є повним диференціалом.
Криволінійний інтеграл від точки (1,-1) до точки (1,1) будемо обчислювати вздовж прямої x=1.
В прямокутній СК контур інтегрування має вигляд
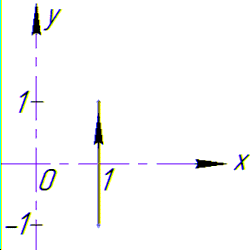
Тут маємо лише один проміжок інтегрування
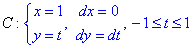
Обчислимо заданий криволінійний інтеграл:
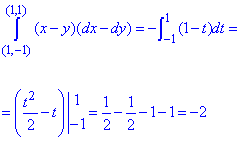
Завдання 5 Переконавшись, що підінтегральний вираз є повним диференціалом, обчислити криволінійний інтеграл
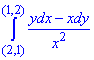
вздовж шляхів, що не перетинають вісь Oy.
Розв'язання: Маємо підінтегральний вираз:
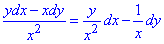
Звідси P=P(x,y)=y/x2, Q=Q(x,y)=-1/x.
Обчислимо часткові похідні функцій P(x,y), Q(x,y):
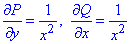
похідні рівні, тому підінтегральний вираз є повним диференціалом.
Криволінійний інтеграл від точки (2,1) до точки (1,2) будемо обчислювати вздовж прямих x=2 і y=2.
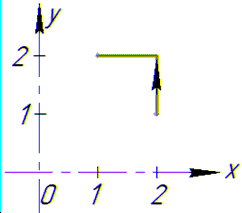
Запишемо як зміняться межі інтегралу та диференціали
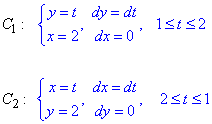
Обчислимо заданий криволінійний інтеграл:
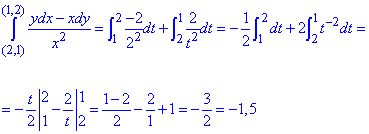
Завдання 6 Переконавшись, що підінтегральний вираз є повним диференціалом, обчислити криволінійний інтеграл
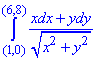
вздовж кривих, що не проходять через початок координат.
Розв'язання: Підінтегральний вираз розіб'ємо на суму двох:
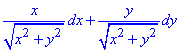
Виписуємо похідні при диференціалах
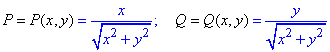
Знайдемо часткові похідні першого порядку функцій P, Q:
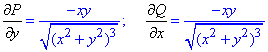
Порівнянням значень робимо висновок що маємо повний диференціал під інтегралом.
Заданий криволінійний інтеграл від точки (1,0) до точки (6,8) будемо обчислювати вздовж прямих y=0 і x=6, тобто на двох інтервалах
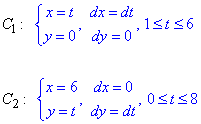
В декартовій площині контур інтегрування має вигляд
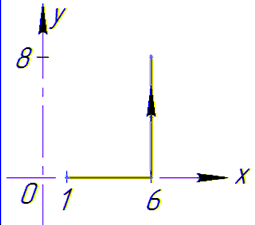
Криволінійний інтеграл рівний 9
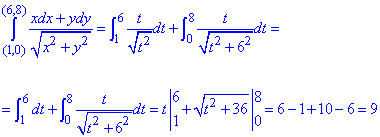
Наведених прикладів на обчислення криволінійного інтегралу від повного диференціалу цілком достатньо, щоб вивчити алгоритм перевірки підінтегральної ф-ї на повний диференціал. Розбивати ділянку між точками на проміжки паралельні осям теж не важко.
Інтегрувати Ви повинні вміти добре перш ніж братися за подібні приклади.
Якщо маєте труднощі в інтегруванні звертайтесь до нас за допомогою, думаю, домовимося!


