Обчислення потоку векторного поля

На попередньому уроці проаналізовані простіші приклади з обчислення потоку векторного поля. Тут завдання ускладнюються поверхнею інтегрування, яка обмежена як одним, так і двома перерізами.
Як наслідок, більше розрахунків меж інтегрування, складніші подвійні інтеграли і самі обчислення. Усі важливі переходи та прийоми добре розписані, а приклади відповідають навчальним програмам більшості ВУЗів України.

ЗАВДАННЯ 8.2 Знайти потік векторного поля 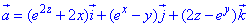через замкнену поверхню S: x²+y²=z², z=1, z=5 (нормаль зовнішня).
Розв'язання:  Поверхня x²+y²=z² - описує частину конуса з вершиною в початку координат, що витягнутий вздовж осі Oz і обмежений площинами z=1, z=5.
В цьому та наступних прикладах для уявлення приведені поверхні інтегрування  та їх проекції в декартову площину
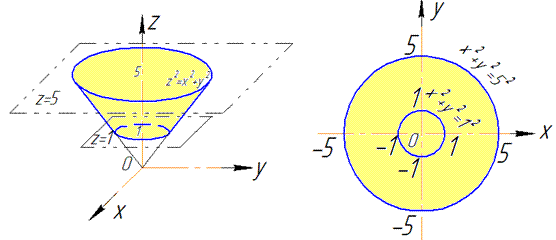В перерізі отримали два кола з радіусами, відповідно, R=1, R=5.
В силу симетрії немає потреби інтегрувати по колу, достатньо знайти межі чверті області інтегрування:

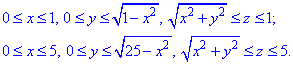
Вкінці результуючий інтеграл множимо на четвірку.
В прикладах на інтегрування по поверхнях потрібно швидко виконувати побудову класичних тіл обертання.
Також необхідно правильно знаходити перетини площинами, інакше правильної відповіді не отримаєте.
Ви маєте вміти вдало враховувати симетричність функцій, їх парність чи непарність.
Обчислимо дивергенцію векторного поля :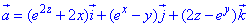

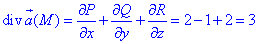
де функції є відповідними множниками при ортах векторного поля
P=P(x;y;z)=e^2z+2x, Q=Q(x;y;z)=e^x-y, R=R(x;y;z)=2z-e^2y.
За формулою Остроградського-Гаусса знаходимо потік векторного поля  
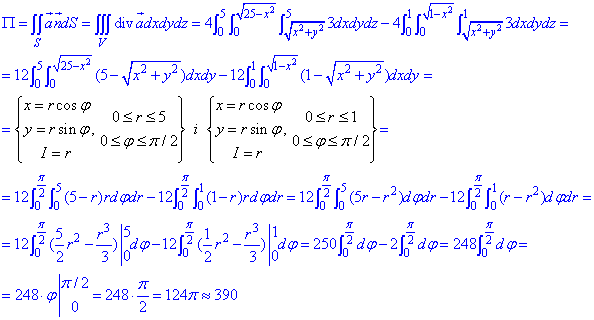З потрійного інтегралу бачимо, що крім того, що потрібно добре вміти вірно розставляти межі інтегрування, знання методу заміни змінних теж важливе. 
Без цього Ви зупинитеся на середині інтегралу і не будете знати, як звести інтеграл до кінцевого значення.

ЗАВДАННЯ 8.4 Обчислити потік векторного поля 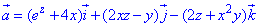через замкнену поверхню S: x²+y²=6z, z=1 (нормаль зовнішня).
Розв'язання: Поверхня x²+y²=6z - коловий параболоїд з вершиною в початку координат, що витягнутий вздовж осі Oz і обмежений площиною z=1.
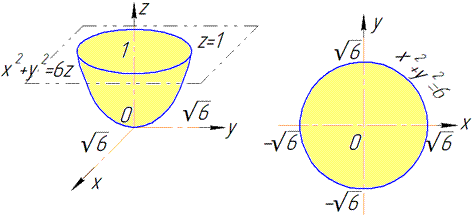В перерізі отримали коло з радіусом рівним кореню з шести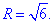
Як  знати, що отримаємо в перерізі площиною?
Хто добре читав теорію, той робить це автоматично а загалом в рівняння поверхні  x²+y²=6z підставляємо площину z=1.
В результаті отримаємо рівняння кола x²+y²=6.
Справа маємо квадрат радіуса, ось і весь аналіз. І така схема справедлива для цілого класу розглянутих задач.
Як бачимо з рисунку чверть області V обмежена  межами:

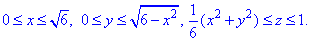
Як і в попередньому завданні, тут враховуємо парність всіх функцій.
Це дозволяє спростити саме інтегрування і не розбивати домінуючий інтеграл на декілька з однаковим кінцевим значенням.
Враховуючи це, результат помножимо на 4. 
Але до нього ще слід дійти, тому спершу обчислюємо дивергенцію векторного поля :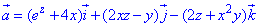 

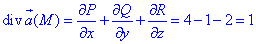
де функції P, Q, R приймають значення
P=P(x;y;z)=e^z+4x, Q=Q(x;y;z)=2xz-y, R=R(x;y;z)=-2z-x²y.
Обчислюємо потік векторного поля  за відомою формулою:
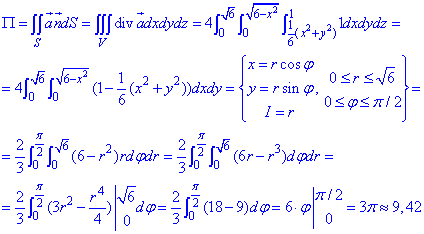Для більшості наведених прикладів перехід до полярної системи координат під інтегралом дозволяє спростити подальше їх знаходження.

Детально зупинятися не будемо, в формулі розписані всі етапи інтегрування та заміни, тож аналізуйте самостійно.

ЗАВДАННЯ 8.7 Знайти потік векторного поля 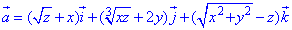через замкнену поверхню S: 2(x²+y²)=z², z=2, z=6 (нормаль зовнішня).
Розв'язання: Рівняння 2(x²+y²)=z² описує конус з вершиною в початку координат (0;0;0), що витягнутий вздовж осі Oz і обмежений площинами z=2, z=6 за умовою.
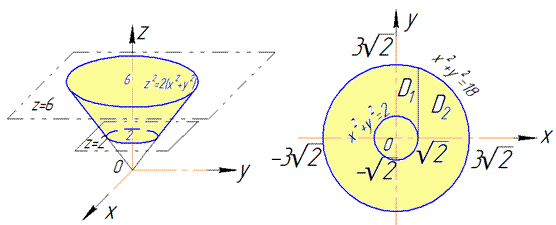В перерізі отримали кола з радіусами, відповідно корінь з двох та вісімнадцяти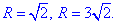
В силу симетрії розглядаємо чверть області V, що обмежена поверхнями:

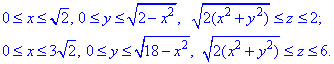
Результат інтегрування помножимо на 4.
Визначаємо дивергенцію векторного поля :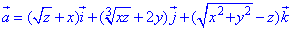

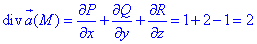
де функції задаються залежностями

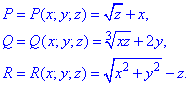
За формулою Остроградського-Гаусса знаходимо потік поля :
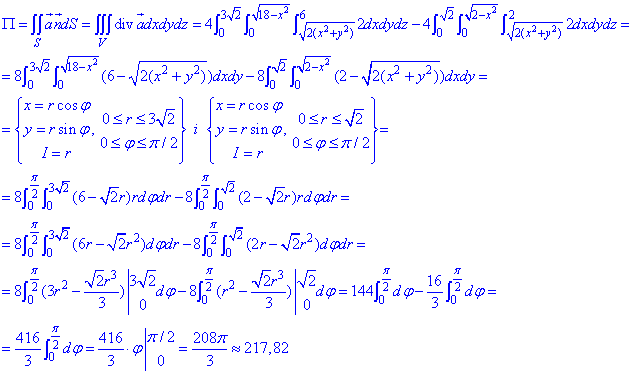Формули не з легких, проте доволі поширені на практиці, тому не спішіть та добре проаналізуйте розстановку меж та заміну змінних.
Застосування переходу до полярної СК дозволяє звести кореневі функції до показникових.

ЗАВДАННЯ 8.8 Обчислити потік векторного поля 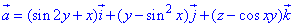через замкнену поверхню S: x²+y²+z²=4x-2y-4 (нормаль зовнішня).
Розв'язання: Зведемо поверхню x²+y²+z²=4x-2y-4 до канонічного вигляду
x²-4x+4+y²+2y+1+z²=4+1-4, (x-2)²+(y+1)²+z²=1 - сфера з центром (2; -1; 0) і радіусом R=1.
Її графік та проекція на площину Oxy можна зобразити рисунком
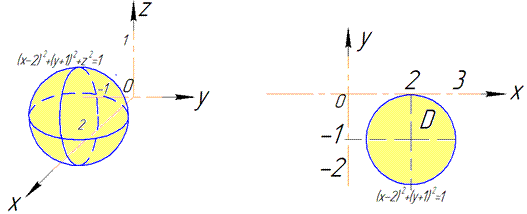Як можна бачити з рисунку, 1/8 поверхні сфери задається границями: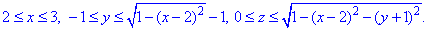

Тут врахували парність функцій, тому інтеграл будемо множити на 8 (верхня і нижня півсфери).
Дивергенцію векторного поля 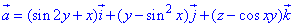 знаходимо за формулою:

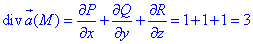
де P=P(x;y;z)=sin(2y)+x, Q=Q(x;y;z)=y-sin²(x), R=R(x;y;z)=z-cos(x*y).
Далі інтегруванням обчислюємо потік  поля : 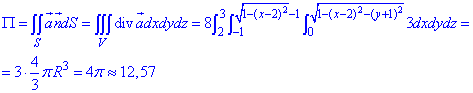де R=1 - радіус сфери.
Так як тут підінтегральна функція рівна сталій, то потрійний інтеграл не що інакше, як об'єм сфери з радіусом 1, розділений на 8 (згідно спрощень).
На основі вище розглянутих задач, спробуйте самостійно знайти потрійний інтеграл та переконатися в правильності міркувань.

ЗАВДАННЯ 8.14 Знайти потік векторного поля 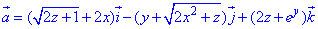через замкнену поверхню S: 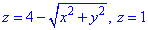, (нормаль зовнішня).
Розв'язання: Поверхня 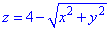задає конус з вершиною в (0;0;4), що витягнутий вздовж осі Oz вниз і обмежений площиною z=1.
Графічно поверхню інтегрування можна уявити з наступних рисунків
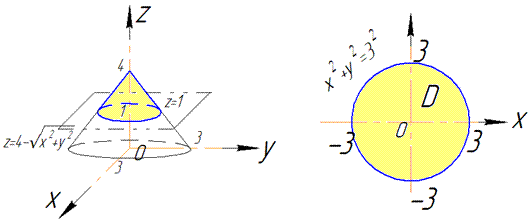В перерізі z=1 отримаємо коло з радіусом R=3. В силу симетрії чверть області V задається наступними межами:

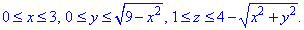
Не забуваємо, що при цьому потрібно інтеграл домножити на 4.
Знаходимо дивергенцію поля :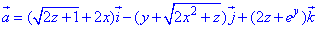

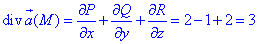
взявши за функції P,Q,R відповідні коефіцієнти поля

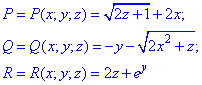
Потік векторного поля знаходимо за формулою Остроградського-Гаусса:
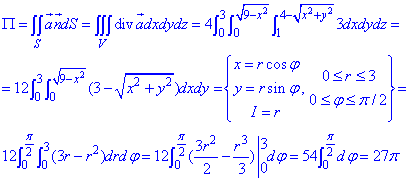Потрійний інтеграл не важкий в плані обчислень, і схеми застосування заміни змінних та зведення до простого вигляду добре розписані в попередніх пунктах.
Потік рівний П=27Pi.

ЗАВДАННЯ 8.15 Обчислити потік векторного поля 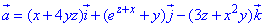через замкнену поверхню S: 2y-x+z=2, x=0, y=0, z=0 (нормаль зовнішня).
Розв'язання: Рівняння 2y-x+z=2, -x/2+y/1+z/2=1- описує площину, яка є однією з граней трикутної піраміди.
Щоб краще це уявити розгляньте наступні рисунки до задачі.
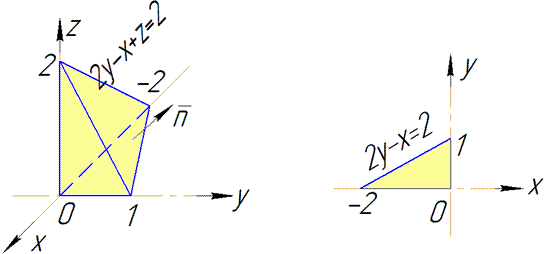З побудови бачимо, що область V обмежена поверхнею:

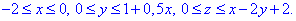
Такий аналіз дозволяє правильно розставити межі в потрійному інтегралі.
Обчислюємо дивергенцію векторного поля :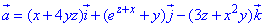

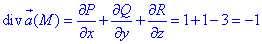
де P=P(x;y;z)=x+4yz, Q=Q(x;y;z)=e^z+x+y, R=R(x;y;z)=-3z-x²y.
Для знаходження потоку  поля  застосовуємо формулу Остроградського-Гаусса:

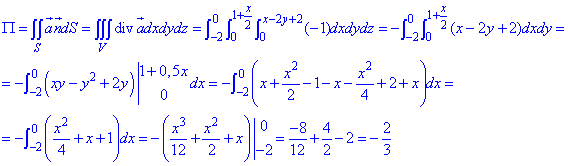
Тут все ясно, оскільки заміни змінних не використовували, а повторне інтегрування не складне.

ЗАВДАННЯ 8.16 Знайти потік векторного поля 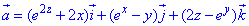через замкнену поверхню S: x²+y²=z², z=1, z=5 (нормаль зовнішня).
Розв'язання: Поверхня x²+y²=z² описує конус з вершиною у (0;0;0), що витягнутий вздовж осі Oz вгору і обмежений площинами z=1, z=5.
Схематично це можна зобразити наступним чином

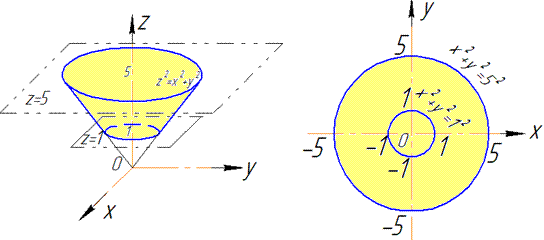
В перерізі отримали 2 кола з радіусами, відповідно, R=1, R=5.
В силу симетрії, чверть області V описуємо межами:

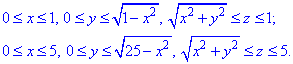
Інтеграл при цьому слід множити на 4.
Через часткові похідні знаходимо дивергенцію поля :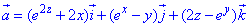
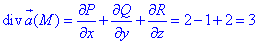, де
тут P=P(x;y;z)=e^2z+2x, Q=Q(x;y;z)=e^x+y, R=R(x;y;z)=2z-e^y.
І найважча частина завдання, це знаходження подвійного інтегралу для визначення потоку  поля :

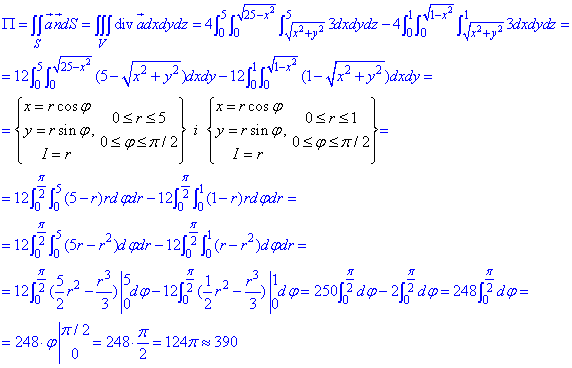
Інтеграл не з легких, тому уважно розберіть як розставлені межі, проаналізуйте ефективність заміни змінних при спрощенні повторного інтегралу.

ЗАВДАННЯ 8.25 Обчислити потік векторного поля 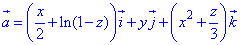через замкнену поверхню S: 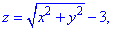z=-1 (нормаль зовнішня).
Розв'язання: Аналіз рівняння 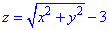-показує, що задано конус з зміщеною відносно початку координат вершиною (0;0;-3), який витягнутий вздовж осі Oz вгору і обмежений зверху площиною z=-1.
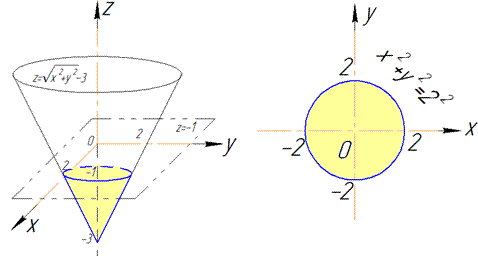В перерізі  маємо коло з радіусом R=2.
Чверть області V описуємо наступними межами:

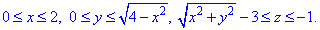
Правильно знайдені межі грають визначальну роль при інтегруванні, тож пам'ятайте що це одна з відповідальних частин наведених розрахунків.
Результат інтегрування не забувайте множити на 4.
Дивергенцію  поля 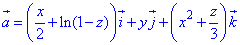 через часткові похідні рівна:

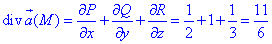
тут враховано P=P(x;y;z)=x/2+ln(1-z), Q=Q(x;y;z)=y, R=R(x;y;z)=x²+z/3.
За наведеною формулою  обчислюємо потік векторного поля :
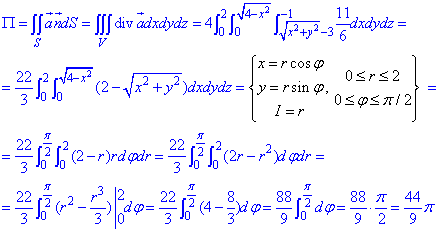Перехід від повторного до подвійного визначеного інтегралу краще робити через наведену заміну змінних, решта все зводиться до простих табличних формул інтегрування та визначення значень на межах.
Будьте уважні при розрахунках, в першу чергу перевіряйте правильність розстановки меж. Далі завчіть заміну змінних, яка тут наведена, та застосовуйте її в прикладах, що подібні за конструкцією до розглянутих.
При обчисленні  інтегралів перевіряйте себе на кожному кроці, найменша помилка при переходах на початку приведе до неправильної відповіді вкінці розрахунків.