Даний метод є другим по простоті застосування після безпосереднього методу інтегрування. Він базуєься на розкладі підінтегральної функції на суму таких функцій, від яких первісну можна знайти за допомогою табличних інтегралів.
Наведу Вам декілька прикладів для ознайомлення з інтегруванням методом розкладу.
Приклад 1. Знайти інтеграли
а) 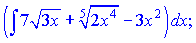
Розв'язання: Інтеграл переписуємо у вигляді суми простих степеневих функцій, після чого кожну з них інтегруємо
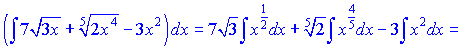
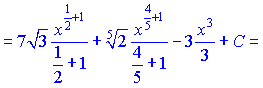
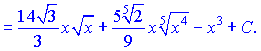
б) 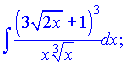
Розв'язання:Піднесемо до третього степеня дужку в чисельнику
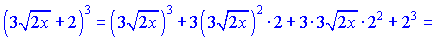
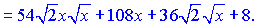
Поділимо знайдений чисельник на знаменник та розпишемо результат через степеневі залежності
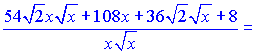
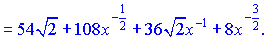
Далі проінтегруємо отримані доданки
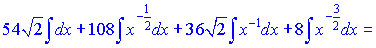
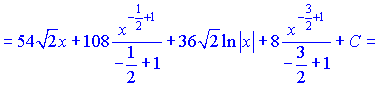
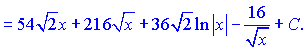
в) 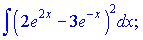
Розв'язання: Піднесемо до квадрату вираз, що містить експоненти та знайдемо неозначений інтеграл за табличною формулою
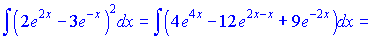
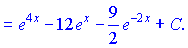
Експоненту з усіх функцій, напевно найлегше інтегрувати.
г) 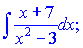
Розв'язання:Розкладемо дробову функцію у вигляді суми двох
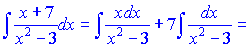
Далі вніссши змінну в першому інтегралі під диференціал, а в другому записавши знаменник у вигляді різниці квадратів, прийдемо до табличних формул інтегрування. Це дає можливість швидко отримати у відповідь логарифми наступних функцій
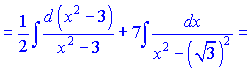
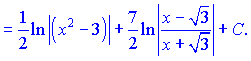
Дану методику рекомендуємо вивчити, в практичних завданнях наведена схема зустрічається доволі часто.
д) 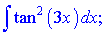
Розв'язання:Проведемо тригонометричні маніпуляції з тангенсом, щоб звести його під формли інтегрування.
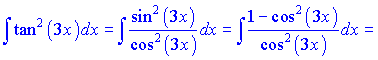
В результаті неозначений інтеграл рівний квадрату тангенса мінус змінна
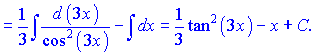
е) 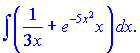
Розв'язок.Розпишемо підінтегральний вираз у вигляді суми окремих доданків
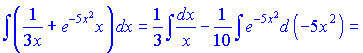
Далі знаходимо відповідні функціям формули та інтегруємо
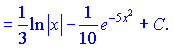
Таким чином, якщо мати таблицю основних інтегралів під рукою, то розв'язування подібних прикладів – це вже справа навичків. Чим більше подібних прикладів Ви розв'яжете, тим легше буде в освоєнні подальших розділів інтегрування.


