Данный метод является вторым по простоте применения после непосредственного метода. Он базируется на расписании подинтегральной функции на сумму таких функций, от которых первоначальную можно найти с помощью табличных интегралов.
Приведу Вам несколько примеров для ознакомления с интегрированием методом разложения.
Примеры.
Найти интегралы
а) ![]()
б) 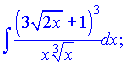
в) ![]()
г) ![]()
д) ![]()
е) 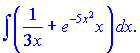
Решение.
а) Интеграл переписываем в виде суммы простых интегралов
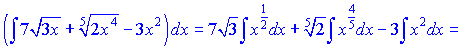
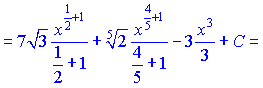
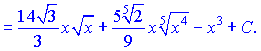
б) Поднесем до третьей степени числитель
![]()
![]()
Разделим найден числитель на знаменатель
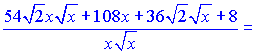
![]()
и проинтегрируем
![]()
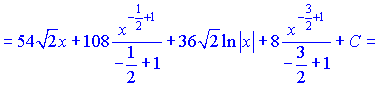
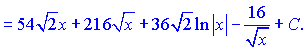
в) Поднесем к квадрату и проинтегрируем
![]()
![]()
г) Разложим в виде суммы двух интегралов
![]()
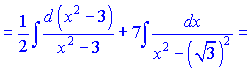
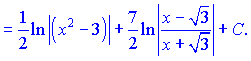
д) Проведем тригонометрические манипуляциии
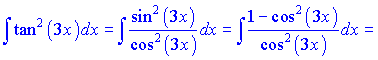
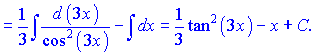
е) Распишем подынтегральная выражение в виде суммы
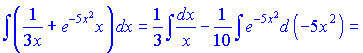
![]()
Таким образом, если иметь таблицу основных интегралов под рукой, то решения подобных примеров - это уже дело навыков. Чем больше подобных примеров Вы решите, тем легче будет в освоении последующих разделов интегрирования.


