Формула Остроградського-Гаусса. Потік векторного поля

Формула Остроградського-Гаусса має широке застосування в математиці, фізиці, хімії. Далі будуть наведені відповіді до прикладів на інтегрування, що передбачають знаходження потоку векторного поля через дивергенцію. В більшості завдань обчислення подвійних інтегралів передбачає заміну змінних, а точніше - перехід до полярної системи координат. Це спрощує підінтегральні вирази, однак веде до перерахунку меж інтегрування. На словах це важко зрозуміти, потрібно аналізувати наведені приклади на формулу Остроградського-Гаусса.

ЗАВДАННЯ 7.1 Знайти потік векторного поля 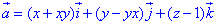через частину поверхні S:
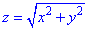, що вирізається площиною P: z=2 (нормаль зовнішня до замкненої поверхні, утвореної даними поверхнями).
Розв'язання: Рівняння 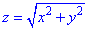- конічна поверхня з вершиною (0;0;0), яка витягнута вздовж осі Oz.
z=2 - площина, яка паралельна до площини Oxy. (шапка).
Наведені поверхню та площину зобразимо в просторі

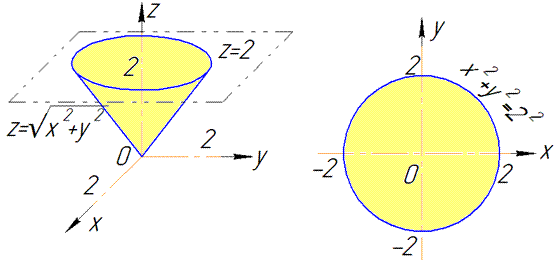
В перерізі з конусом отримаємо коло радіуса R=2.
Як бачимо з рисунку чверть області V задається наступними межами:

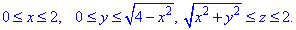
Тут врахували парність всіх функцій, тому результат помножимо на 4.
Обчислимо дивергенцію векторного поля :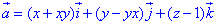

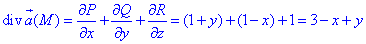
де P=P(x;y;z)=x+xy, Q=Q(x;y;z)=y-yx, R=R(x;y;z)=z-1.
Останні функції беремо з a.
Знайдемо потік  поля за формулою Остроградського-Гаусса: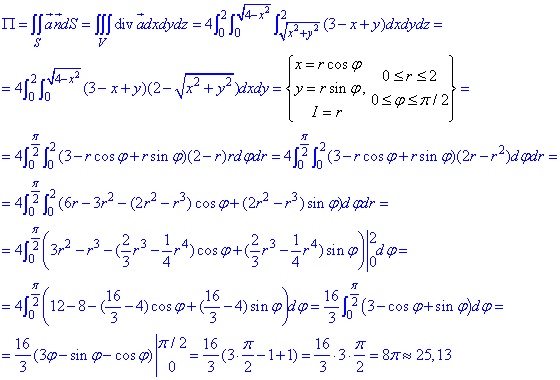

ЗАВДАННЯ 7.3 Знайти потік векторного поля 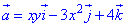через частину поверхні S: 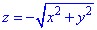, що вирізається площиною P: z=-1 (нормаль зовнішня до замкненої поверхні, утвореної даними поверхнями).
Розв'язання: 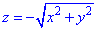- конічна поверхня (нижня частина) з вершиною (0;0;0), яка витягнута вздовж осі Oz.
z=-1 - площина, яка паралельна до площини Oxy.

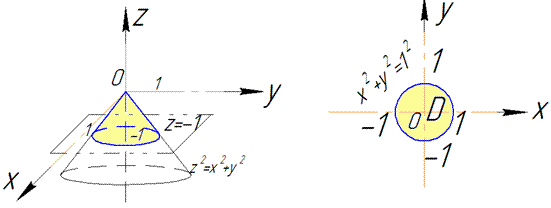
В перерізі з конусом отримаємо коло радіуса R=1.
Як бачимо з рисунку чверть області V задається наступними межами: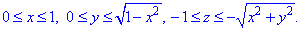
Тут врахували парність всіх функцій, тому результат будемо множити на 4.
Знаходимо дивергенцію векторного поля :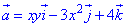

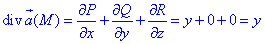
де P=P(x;y;z)=xy, Q=Q(x;y;z)=-3x², R=R(x;y;z)=4.
За формулою Остроградського-Гаусса обчислюємо потік  поля  :

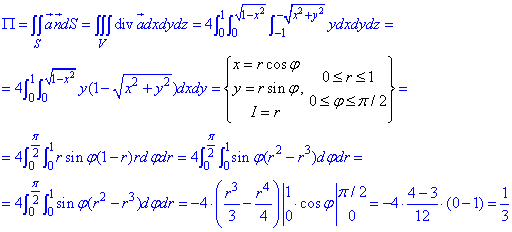
Перехід до полярної системи координат значно спрощує знаходження подвійного інтегралу.

ЗАВДАННЯ 7.5 Обчислити потік векторного поля 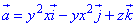через частину поверхні S: 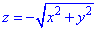, що вирізається площиною P: z=-5 (нормаль зовнішня до замкненої поверхні, утвореної даними поверхнями).
Розв'язання: Рівняння 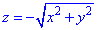 - задає конічну поверхню з вершиною (0;0;0), яка витягнута вздовж осі Oz.
z=-5- площина, яка паралельна до площини Oxy.

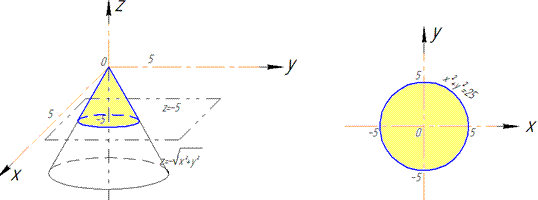
В перерізі з конусом отримаємо коло радіуса R=5. Як бачимо з рисунку чверть області V задається наступними межами: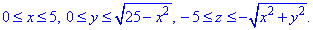
Тут врахували парність всіх функцій, тому результат будемо множити на 4.
Дивергенція векторного поля 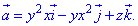 рівна

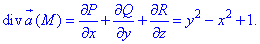
де P=P(x;y;z)=y²x, Q=Q(x;y;z)=-yx², R=R(x;y;z)=z.
Потік  поля  знаходимо переходом до подвійного інтегралу за формулою: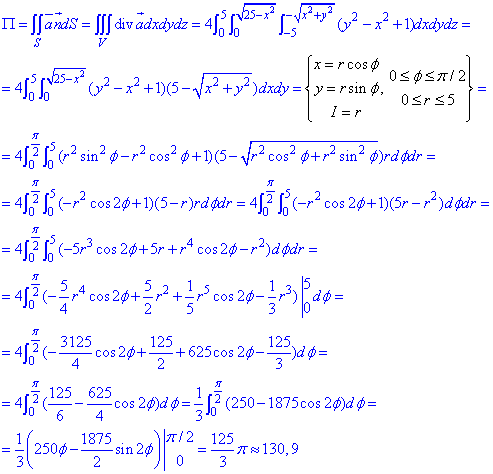

Знову маємо заміну змінних під інтегралом. Цей прийом є незамінним при знаходженні інтегралів по поверхнях обертання - підінтегральні функції та межі спрощуються, відпадає потреба боротися з коренями та вишукувати екзотичні формули інтегралів з довідників

ЗАВДАННЯ 7.7 Знайти потік векторного поля 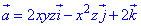через частину поверхні S: 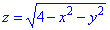, що вирізається площиною P: z=0 (нормаль зовнішня до замкненої поверхні, утвореної даними поверхнями).
Розв'язання: Приведемо поверхню 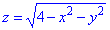до канонічного вигляду z²=4-x²-y², x²+y²+z²=2²- сфера (верхня половина) з центром (0;0;0) і радіусом R=2.
z=0 - площина, яка паралельна до площини Oxy.

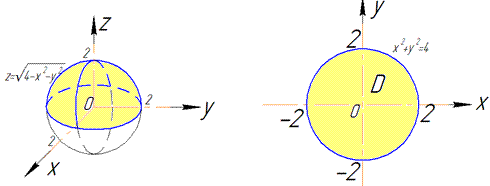
В перерізі зі сферою отримаємо коло з центром у (0;0;0) і радіусом R=2.
З рисунку бачимо чверть області V задається наступними межами: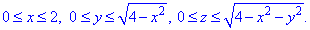
Тут врахували парність всіх функцій, тому результат будемо множити на 2.
Обчислюємо дивергенцію :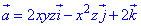

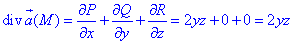
де P=P(x;y;z)=2xyz, Q=Q(x;y;z)=-x²z, R=R(x;y;z)=2.
Потік векторного поля  визначаємо через формулу Остроградського-Гаусса:

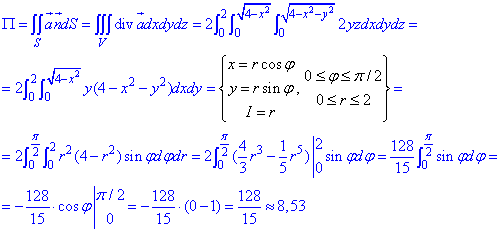
ЗАВДАННЯ 7.8 Знайти потік векторного поля 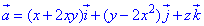через частину поверхні S: 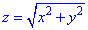, що вирізається площиною P: z=4 (нормаль зовнішня до замкненої поверхні, утвореної даними поверхнями).
Розв'язання: Рівняння 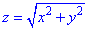 описує конічну поверхня з вершиною в початку координат (0;0;0), яка витягнута вздовж осі Oz.
Переріз z=4 - площина, яка паралельна до площини Oxy.

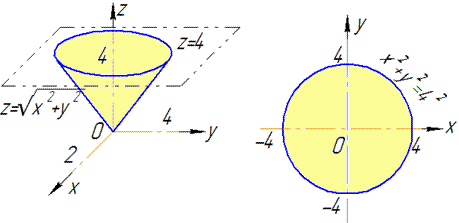
В перерізі з конусом отримаємо коло радіуса R=4.
Як бачимо з рисунку чверть області V задається наступними межами: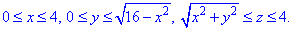
Парність всіх функцій дозволяє шукати інтеграл на меншій поверхні, але результат потрібно буде помножити на 4. 
Дивергенцію векторного поля 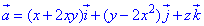 визначаємо за формулою:

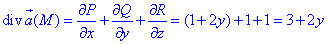
де P=P(x;y;z)=x+2xy, Q=Q(x;y;z)=y-2x², R=R(x;y;z)=z.
Знайдемо потік  поля :

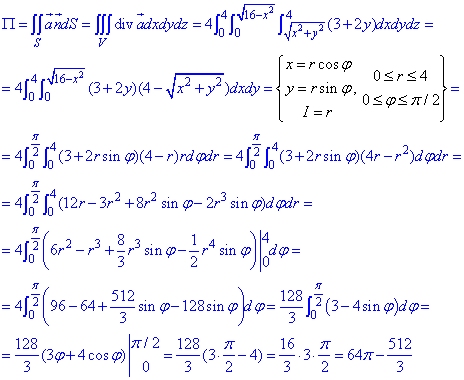
ЗАВДАННЯ 7.14 Визначити потік векторного поля 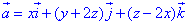через частину поверхні S: 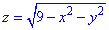, що вирізається площиною P: z=0 (нормаль зовнішня до замкненої поверхні, утвореної даними поверхнями).
Розв'язання: Рівняння 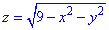 - описує верхню частину півсфери з центром (0;0;0) і радіусом R=3.
В перерізі з площиною z=0 отримаємо коло радіуса R=3.

Як бачимо з рисунку чверть області V задається наступними межами: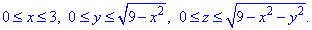

Врахування парності функцій дозволяє записати межі лише в чверті області, тому потік необхідно помножити на 4.
Порахуємо дивергенцію поля :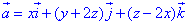

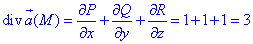
де P=P(x;y;z)=x, Q=Q(x;y;z)=y+2z, R=R(x;y;z)=z-2x.
Застосовуємо формулу Остроградського-Гаусса для визначення потоку векторного поля :

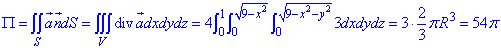
ЗАВДАННЯ 7.15 Знайти потік векторного поля 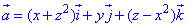через частину поверхні S: 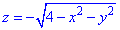, що вирізається площиною P: z=0 (нормаль зовнішня до замкненої поверхні, утвореної даними поверхнями).
Розв'язання: Поверхня 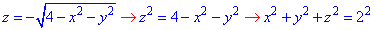- сфера (нижня частина) з центром в початку декартової СК (0;0;0) і радіусом R=2.

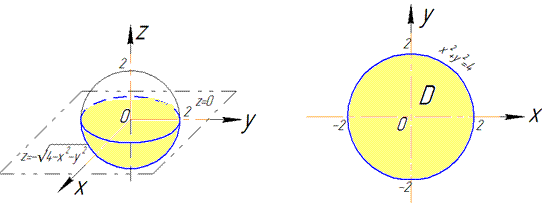
В перерізі площини z=0 зі сферою отримаємо коло радіуса R=2.
Як бачимо з рисунку чверть області V задається наступними межами:
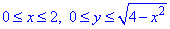і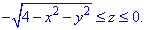
Результат інтегрування необхідно помножити на 4, оскільки  враховуємо парність функцій.
Обчислимо дивергенцію векторного поля :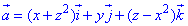

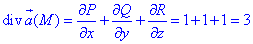
де функції P=P(x;y;z)=x+z², Q=Q(x;y;z)=-y, R=R(x;y;z)=z-x².
Інтегруванням знаходимо потік векторного поля :

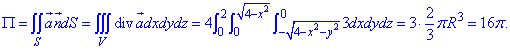
Він рівний P=16Pi.

ЗАВДАННЯ 7.16 Знайти потік векторного поля 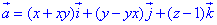через частину поверхні S: 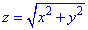, що вирізається площиною P: z=2 (нормаль зовнішня до замкненої поверхні, утвореної даними поверхнями).
Розв'язання: Коренева залежність 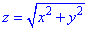- задає конічну поверхню з вершиною в точці (0;0;0), яка витягнута вздовж осі Oz.
z=2 - площина, яка паралельна до площини Oxy.
В перерізі з конусом отримаємо коло радіусом R=2.

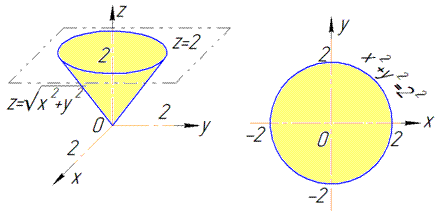
Як бачимо з рисунку чверть області V задається наступними межами: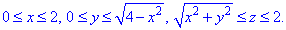

Парність функцій врахована, тому результуючий інтеграл потрібно помножити на четвірку.
Обчислимо дивергенцію векторного поля :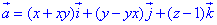

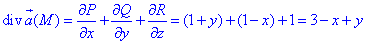
де P=P(x;y;z)=x+xy, Q=Q(x;y;z)=y-yx, R=R(x;y;z)=z-1.
За формулою Остроградського-Гаусса обчислюємо потік :
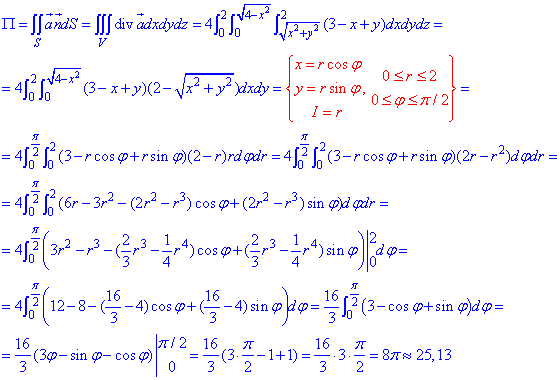Алгоритм обчислення подвійних інтегралів з прикладу в приклад не змінюється, перехід до полярної системи координат при інтегрування Ви повинні добре знати, такий прийом дозволяє спростити широкий клас інтегралів, а подальші обчислення звести до простих інтегралів від показникових функцій та тригонометричних. В окремих випадках Вам доведеться застосовувати формули пониження степенів для переходу від квадратів синусів та косинусів до їх перших степенів. 

ЗАВДАННЯ 7.24 Обчислити потік векторного поля 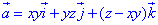через частину поверхні S: 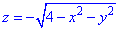, що вирізається площиною P: z=-1 (нормаль зовнішня до замкненої поверхні, утвореної даними поверхнями).
Розв'язання: Перетворюємо рівняння поверхні 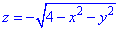до канонічного вигляду z^2=4-x^2-y^2, x^2+y^2+z^2=2^2 - сфера (нижня частина) з центром (0;0;0) і радіусом R=2.
z=-1 - площина, яка паралельна до площини Oxy.

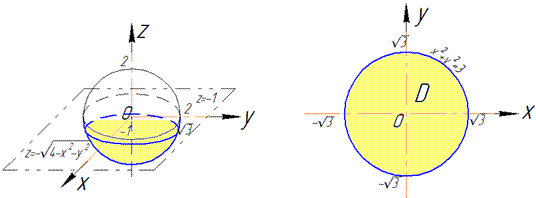
В перерізі зі сферою отримаємо коло радіусом корінь з трьох .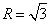
Як бачимо з рисунку чверть області V задається наступними межами: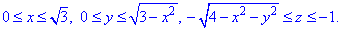

В силу парності функцій, виписуємо межі лише на 1/4 поверхні сфери.
Дивергенція векторного поля 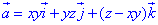 через часткові похідні становить:

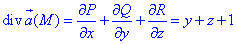
де функції рівні P=P(x;y;z)=xy, Q=Q(x;y;z)=yz, R=R(x;y;z)=z-xy.
Потік векторного поля  визначаємо з подвійного інтегралу:

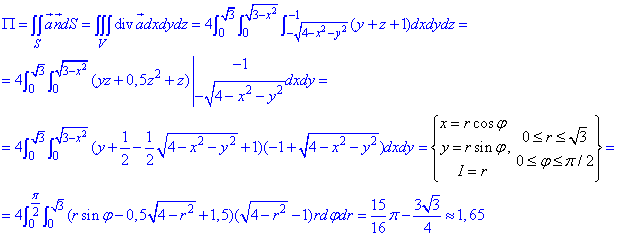
На цьому ознайомлення з прикладами на знаходження потоку векторного поля не завершується, більше готових відповідей Ви знайдете на сусідніх сторінках.