Відношення площ подібних трикутників

Теорема: відношення площ подібних трикутників пропорційне квадрату лінійних розмірів відповідних сторін.

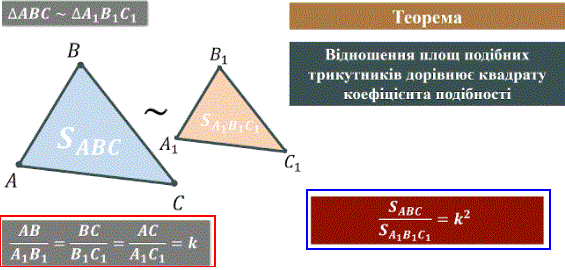
На уроці розберемо кілька завдань, які розв'язують з властивостей подібності трикутників. Тому добре запам'ятайте наведену вище схемку.
В усіх відібраних прикладах із ЗНО підготовки потрібно скласти та розв'язати рівняння пропорційності площ до лінійних розмірів. Приклади на трикутники такого типу обчислюють в 10, 11 класі шкільної програми. Далі Ви їх зустріните в тестах, вступних іспитах та на перших курсах навчання у ВУЗах. Методика обчислень достатньо добре розписана, тому алгоритми обчислень запам'ятайте та самостійно застосовуйте до подібних завдань.

Тема: Перетворення фігур

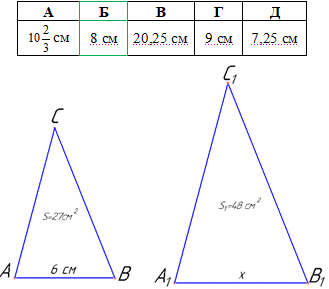
Приклад 43.10 Площі двох подібних трикутників дорівнюють 27 см² і 48 см². Одна зі сторін першого трикутника дорівнює 6 см. Знайти відповідну їй сторону другого трикутника.

Розв'язування: Завдання на трикутники найпоширеніші в курс геометрії і частина з них обчислюється за ознаками подібності. Як саме пропорційність впливає на площу, об'єм, довжину дуг Ви повинні знати, тому вкінці пояснень до прикладу вивчіть властивості розмірів.
Нехай маємо перший трикутник ABC зі стороною AB=6 см, площею S=27 см², а також другий трикутник A₁B₁C₁ зі стороною A₁B₁=x, площею S₁=48 см².
Площі подібних фігур пропорційні до квадратів їх лінійних розмірів.
Складемо відношення площ та знайдемо невідому сторону трикутника x:

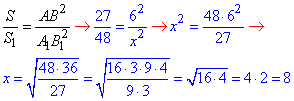
звідси A₁B₁=8 см.
Відповідь: 8 см – Б.

На загал, Ви повинні знати, що площі фігур пропорційні їх лінійним розмірам.
Периметри пропорційні самим лінійним розмірам фігур при перетвореннях подібності, а об'єми пропорційні лінійним розмірам у кубі. Для прикладу якщо куб паралелепіпед зі сторонами 2, 3, 4 метри з об'ємом V=2•3•4=24 м³ збільшити у два рази, то за властивостями подібності об'єм збільшиться у k=2^3=8 разів, а саме
V1=4•6•8=192 м³.
Відношення об'ємів рівне
k=V1/V=192/24=8.
Якщо лінійн розміри змінилися у будь-яке більше нуля k раз, то периметр фігури зміниться лінійно p1=k•p,
площа за квадратичною залежністю S1=k^2•S,
об'єм змінюється за кубічним законом лінійних розмірів
V1= k^3•V.
Пам'ятайте про це та використовуйте в розрахунках!

Приклад 43.30 Середня лінія трикутника відтинає від нього трапецію, площа якої дорівнює 21 см². Знайти площу даного трикутника.

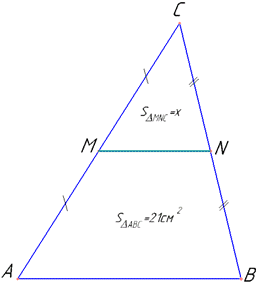
Розв'язування: Маємо трикутник ABC, у якого MN – середня лінія, що сполучає середини сторін AC і BC, відповідно.
Відрізок MN відтинає від трикутника ABC трапецію AMNB, площа якого S_AMNB=21 см² (за умовою) і трикутник MNC подібний до трикутника ABC (за властивістю MN||AB і AB=2MN).
Нехай S_ΔMNC=x – площа трикутника MNC, тоді площа трикутника ABC:
S_ΔABC=x+21.
Складемо рівняння пропорційності площ та розв'яжемо його відносно x:

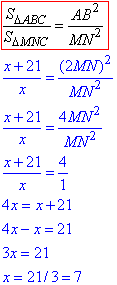
Тут маємо простий дріб, з якого легко виражаємо невідому.
S_ΔABC=7+21=28 (см²) – площа трикутника ABC.
Відповідь: 28 см².

Приклад 43.31 Продовження бічних сторін AB і CD трапеції ABCD перетинаються у точці E.

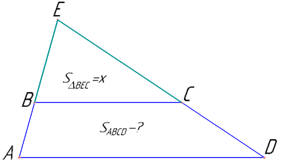
Знайти площу трапеції, якщо BC:AD=3:5, а площа трикутника AED дорівнює 175 см².
Розв'язування: Маємо трапецію ABCD (AD||BC), у якої BC:AD=3:5, а продовження бічних сторін AB і CD трапеції ABCD перетинаються у точці E (за умовою).
Отримаємо трикутник AED, площа якого S_ΔAED=175 см² і трикутник BEC, який буде подібний до трикутника AED, оскільки AD||BC (за властивістю).
Нехай S_ΔBEC=x – площа трикутника BEC, тоді площа трапеції ABCD:
S_ABCD=S_ΔAED-S_ΔBEC=175-x.
Оскільки BC:AD=3:5, то за властивістю пропорції 3AD=5BC, або AD=5/3•BC.
Пригадаємо, що площі пропорційні квадрату лінійних розмірів подібних фігур.
Складемо рівняння на відношення площ та обчислимо його:

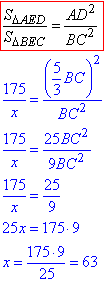
S_ABCD=175-63=112 (см²) – площа трапеції ABCD.
Відповідь: 112 см².

Приклад 43.32 Пряма, паралельна до сторони AB трикутника ABC, перетинає його сторону AC у точці E, а сторону BC – у точці F.

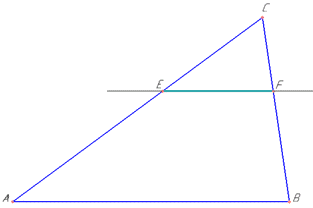
Знайти площу трикутника CEF, якщо AE:EC=3:2, а площа трикутника ABC дорівнює 75 см².
Розв'язування: Розглянемо трикутник ABC, площа якого S_ΔABC=75 см².
За умовою завдання AC=AE+EC і BC=BF+FC.
Оскільки вдношення сторін рівне AE:EC=3:2 (за умовою), то за властивістю пропорції маємо 3EC=2AE, або AE=1,5EC.
Підставляємо в попередню формулу AC=1,5EC+EC=2,5EC.
Розглянемо трикутники ABC і EFC, у яких є спільний кут C, а також EF||AB за умовою.
Звідси випливає, що ΔABC і ΔEFC подібні.
Позначимо S_ΔEFC=x – площа ΔEFC.
Можемо скласти рівняння пропорційності площ та розв'язати його відносно x:

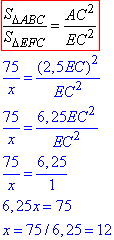
Площа трикутників пропорційна квадрату лінійних розмірів сторін, тому правильним є не тільки відношення AC²/EC² в правій стороні виділеної формули але й BC²/FC².
Пам'ятайте про це при розв'язуванні задач на трикутники.
На основі обчислень записуємо S_ΔEFC=12 см² – площу трикутника EFC.
Відповідь: 12 см².

Якщо в навчанні Ви зустрінете цікаві приклади на подібність трикутників, якими можна доповнити та розширити цей урок, тоді просимо надсилати їх нам. Ми їх красиво оформимо та опублікуємо, щоб приклади були доступні великій аудиторії учнів, студентів та батьків.