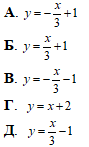Встановити образ прямої при симетрії та паралельному перенесенні

На попередніх уроках розглядали приклади на знаходження ескізів точок, зараз розберемо готові відповіді на паралельне перенесення та симетрію прямих, а в наступних уроках задачі на геометричні перетворення для кіл, парабол, трикутників. Завдання підібрано на основі програми підготовки до ЗНО підготовки з математики, тому в першу чергу допоможуть на практичних учням 10,11 класів. Щоб підвищити теоретичні знання перегляньте статтю на "Геометричні перетворення та перетворення подібності". Головні властивості, на які просимо звернути увагу та вивчити виділені в поясненнях жирним шрифтом..

Тема: Перетворення фігур

Приклад 43.1 Який з відрізків є образом відрізка AB при русі?

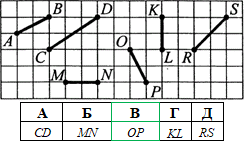
Розв'язування: Рухом (переміщенням) називають перетворення фігури, яке зберігає відстань між точками.
Відрізок AB по довжині рівний лише відрізку OP, тобто відстань між точками як кінцями відрізка є однаковими, тому відрізок OP є образом відрізка AB при русі.
Відповідь: OP – В.

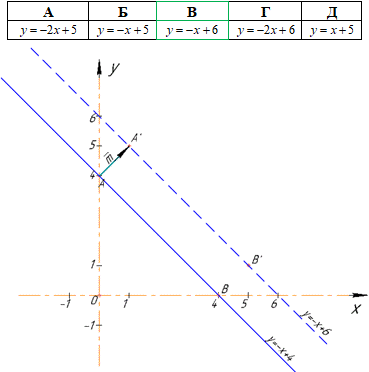
Приклад 43.7 Яка з прямих, зображених на рисунку, може бути образом прямої a при паралельному перенесенні?

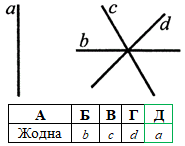
Розв'язування: При паралельному перенесенні пряма переходить у паралельну їй пряму або в себе.
Оскільки жодна з прямих b, c і d не є паралельними до прямої a, то пряма a при паралельному перенесенні (на нульовий вектор) перейшла у саму себе. Отже, пряма a є образом прямої a при заданому паралельному перенесенні.
Відповідь: a – Д.

Приклад 43.11 Встановити образ прямої y=2x+3 при симетрії відносно початку координат.

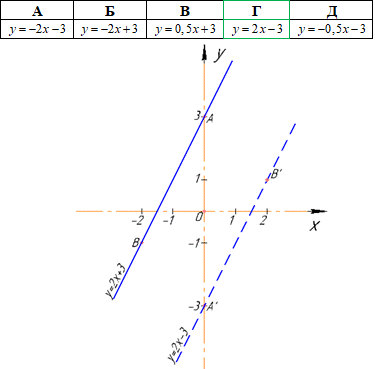
Розв'язування: Маємо пряму y=2x+3, рівняння якої має вигляд y=k•x+b, де k=2 і b=3. Це означає, що пряма перетинає вісь ординат у точці A(0;3). За властивістю центральної симетрії (симетрії відносно точки):
образом прямої, яка не проходить через центр симетрії, є паралельна їй пряма.
Маємо образ прямої з рівнянням y=k1x+b1, де k=k1=2.
Оскільки пряма симетрична відносно початку координат (точки O(0;0)), то образом точки A(0;3) при цій симетрії буде точка A'(0;-3) (координати змінили на протилежні), тоді b1=-3.
Звідси отримали рівняння образу прямої: y=2x-3.
Відповідь: y=2x-3 – Г.

Приклад 43.13 Знайти образ прямої y=-4x-3 при симетрії відносно вісі Oy.

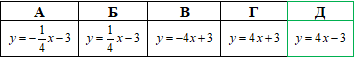
Розв'язування: Знайдемо точки перетину прямої y=-4x-3 з осями координат:
x=0, звідси y=-3, отримали A(0;-3).
y=0, звідси x=-3/4, отримали B(-3/4;0).
За властивістю симетрії відносно вісі Oy:
точки, симетричні відносно осі Oy, мають однакові ординати та протилежні абсциси.
Тому при симетрії відносно вісі Oy точка A(0;-3) залишилася без змін (бо належить цій осі), а точка B(-3/4;0) переходить в точку B'(3/4;0).

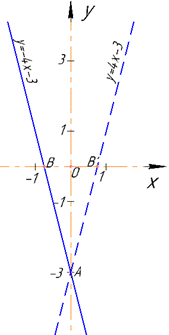
Запишемо рівняння образу прямої, яка проходить через дві точки A(0;-3) і B'(3/4;0), при симетрії відносно вісі Oy:
y=k•x+b,

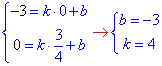
Отримаємо рівняння прямої y=4x-3.
Відповідь: y=4x-3 – Д.

Приклад 43.14 При симетрії відносно прямої y=x пряма y=-4x+4 переходить у пряму…

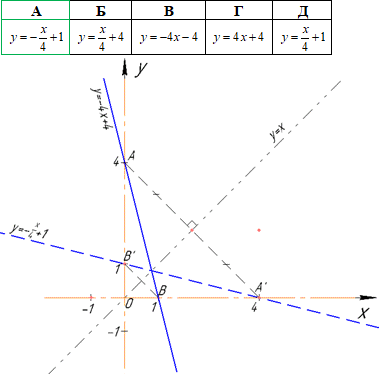
Розв'язування: Знайдемо точки перетину прямої y=-4x+4 з осями координат:
x=0, звідси y=4, отримали A(0;4).
y=0, звідси x=1, отримали B(1;0).
За властивістю симетрії відносно прямої y=x:
у точках, симетричних відносно прямої y=x, ординати та абсциси змінюються місцями.
Тому при симетрії відносно прямої y=x точка A(0;4) переходить в точку A'(4;0), а точка B(1;0) переходить в точку B'(0;1).
Запишемо рівняння образу прямої, яка проходить через дві точки A'(4;0) і B'(0;1), при симетрії відносно прямої y=x: y=k•x+b,

При пдстановці в рівняння прямої, матимемо
 y=k•x+b=-x/4+1.
Відповідь: y=x/4+1 – А.

Приклад 43.16 Встановити образ прямої y=-x+4 при паралельному перенесенні на вектор 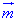(1;1).

Розв'язування: Знайдемо точки перетину прямої y=-x+4 з осями координат:
x=0, звідси y=4, отримали A(0;4).
y=0, звідси x=4, отримали B(4;0).
За властивістю паралельного перенесення на вектор m: до координат точок A(0;4) і B(4;0) додамо відповідні координати вектора m(1;1) і отримаємо координати образів точок A'(1;5) і B'(5;1) при паралельному перенесенні.
Запишемо рівняння образу прямої, яка проходить через дві точки A'(1;5) і B'(5;1):
y=kx+b,

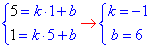
Звідси y=-x+6.
При паралельному перенесенні прямі залишаються паралельними, тому їх кутові коефіцієнти k є рівними і дорівнюють -1.
(Тому для образу прямої достатньо лише взяти одну точку і її паралельно перенести на заданий вектор).
Відповідь: y=-x+6 – В.

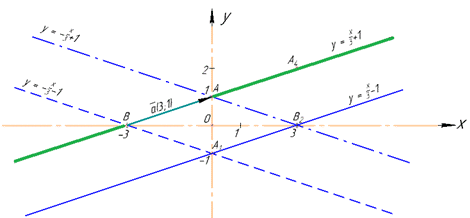
Приклад 43.23 Дано пряму y=x/3+1. Установити відповідність між перетвореннями (1–4) та рівняннями образів даної прямої (А–Д).

Розв'язування: Знайдемо точки перетину прямої y=x/3+1 з осями координат:
x=0, звідси y=1, отримали A(0;1).
y=0, звідси x=-3, отримали B(-3;0).

1. За властивістю симетрії відносно вісі Ox:
точки, симетричні відносно осі абсцис Ox, мають однакові абсциси та протилежні ординати.
Тому при симетрії відносно вісі Ox точка B(-3;0) залишилася без змін (бо належить цій осі), а точка A(0;1) переходить в точку A1(0;-1).
Запишемо рівняння образу прямої, яка проходить через дві точки A1(0;-1) і B(-3;0), при симетрії відносно вісі Ox:
y=k·x+b,

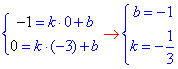
Записуємо шукане рівняння прямої y=-x/3-1. В.

2. За властивістю симетрії відносно осі Oy:
точки, симетричні відносно осі ординат Oy, мають однакові ординати та протилежні абсциси.
При симетрії відносно вісі Oy точка A(0;1) залишилася без змін (бо належить цій осі), а точка B(-3;0) переходить в точку B2(3;0).
Запишемо рівняння образу прямої, яка проходить через дві точки A(0;1) і B2(3;0), при симетрії відносно вісі Oy:
y=k·x+b,

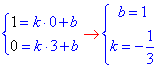
Звідси y=-x/3+1. А.

3. Маємо пряму y=x/3+1, рівняння якої має вигляд y=k·x+b, де k=1/3 і b=1.
Властивість центральної симетрії (симетрії відносно точки):
образом прямої, яка не проходить через центр симетрії, є паралельна їй пряма.
Отже, маємо образ прямої з рівнянням y=k3·x+b3, де k=k3=1/3.
Оскільки пряма симетрична відносно початку координат (точки O(0;0)), то образом точки A(0;1) при цій симетрії буде точка A1(0;-1) (координати змінили на протилежні), тоді b3=-1.
Отримали рівняння образу прямої:
y=x/3-1. Д

4. За властивістю паралельного перенесення на вектор :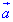
до координат точок A(0;1) і B(-3;0) додамо відповідні координати вектора a(3;1) і отримаємо, відповідно, координати образів точок A4(3;2) і A(0;1) при паралельному перенесенні.
Але отримані точки і так належать заданій прямій y=x/3+1, тому при заданому паралельному перенесенні на вектор a(3;1) задана пряма y=x/3+1 переходить у саму себе. Б.

Далі розберемо розв'язки прикладів на перетворення подібності для кіл, парабол та трикутників.