Квадрат и окружность – две простые фигуры геометрии свойства которых должны знать все. Квадрат является частным случаем четырехугольников, прямоугольников, параллелограммов, ромбов, а отличается от них равными сторонами и прямыми углами.
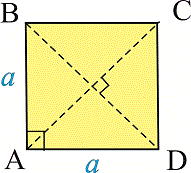
Квадрат наиболее симметричная фигура среди всех четырехугольников.
Свойства квадрата
Свойства квадрата - это основные признаки которые позволяют распознать его среди прямоугольников, ромбов, четырехугольников:
- В квадрата все стороны и углы равны AB=BC=CD=AD.
- Противоположные стороны параллельны между собой
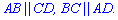
- Углы между соседними сторонами прямые.
- Диалонали квадрата равны и пересекаются под прямым углом.
- Диагонали является одновременно биссектрисами углов квадрата.
- Точка в которой пересекаются диагонали является центром квадрата, кроме этого - центром вписанной и описанной окружности.
- Диагонали делят квадрат на четыре одинаковые равнобедренные прямоугольные треугольники .
Площадь квадрата
Больше примеров в школьном курсе при изучении квадрату связано с вычислением его площади и периметра. Вам может показаться что для вычисления площади достаточно знать одну формулу S=a*a и этого хватит для всех задач, однак это не так. Поскольку быстро информация воспринимается и изучается визуально, то мы объединили все величины квадрата которые Вам придется вычислять и нарисовали простые и понятные рисунки с формулами. Их без трудностей можете скачать по ссилке внизу статьи.
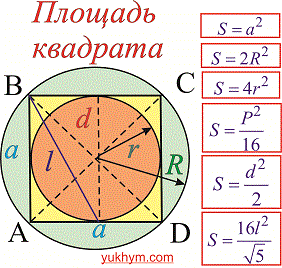
Большинство обозначений Вам понятна, но повторим их снова
a– сторона квадрата;
d– диагональ;
P– периметр;
S– площадь;
R– радиус описанной окружности;
r– радиус вписанной окружности;
l– отрезок изображен на рисунке (часто используется в сложных примерах).
Формулы площади квадрата которые приведены ниже дают возможность вычислять ее через периметр, сторону, диагонали, радиусы .
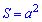
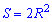
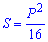
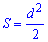
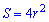
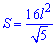
Они не слишком сложные и каждая из них может Вам пригодиться для вычисления площади квадрата.
Периметр квадрата
Что может быть проще вычисления периметра квадрата если конечно известно его стороны. Однако, если задана только диагональ, площадь, радиус то нахождение периметра не так очевидно. Приведенный ниже рисунок содержит самые необходимые формулы для вычисления параметра
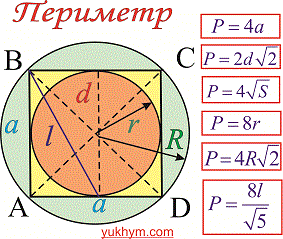
Сами же формулы периметру от различных параметров квадрату привидены ниже
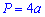
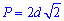
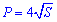
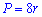
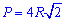
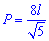
Диагональ квадрата
Диагональ квадрата может бить выражена через радиусы вписанной, описанной окружностей, сторону, периметр, площадь следующими формулам.
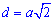
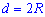
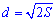

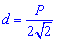
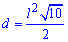
В качестве справочника формул диагонали квадрата можете использовать следующий рисунок.
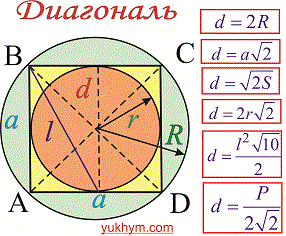
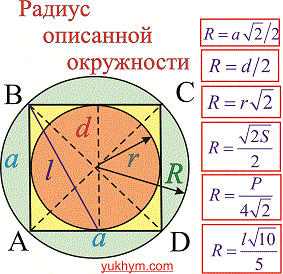
Радиус описанной окружности
Простейшая для вычислений формула радиуса описанной окружности R=d/2, т.е. радиус равен половине диагонали квадрата. Все последующие формулы которые помогут определить радиус описанной окружности содержат корни, однако при вычислениях незаменимы.
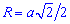
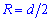
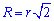
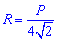
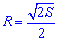
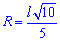
Ниже изображен вспомогательный рисунок с приведенным всеми формулами.
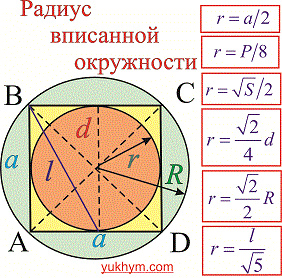
Радиус вписанной окружности в квадрат
Радиус вписанной окружности из рисунка равный половине его стороны.
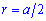
Также он равной одной восьмой части периметра. Зависимости для нахождения радиуса вписанной окружности через площадь, диагональ, радиус описанной окружности содержат иррациональности. Однако и в условиях примеров величины, известные для вычисления радиуса, как правило, заданны с корнями или такими которые легко упрощаются (например 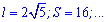 ).
).
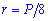
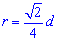
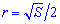
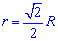
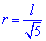
Черновик-подсказка формул радиуса вписанной в квадрат окружности приведена ниже
Если же задано диаметр вписанной или описанной окружности то делим пополам (чтобы получить радиус) и можем применять в приведенных формулах. Это Вы думаю помните.
Бонус для всех школьников и студентов. Все цветные графики с формулами площади квадрата, его периметра, диагонали, радиусов вписанной и описанной окружности Вы можете скачать по ссылке внизу.
Распечатывайте формулы и пользуйтесь в обучении.
{jd_file file==18}
Понравился материал - поделись ссылкой с друзьями.
Посмотреть материалы:
- Прямоугольный треугольник. Задачи
- Площадь треугольника. Формулы
- Периметр и площадь прямоугольника
- Периметр и площадь параллелограмма
- Формулы площади трапеции
- Ромб. Площадь, периметр
{jcomments on}


