В школьном курсе в геометрии среди основных задач значительное внимание уделено примерам вычисления площади и периметра ромба. Вспомним что ромб принадлежит к отдельному классу четырехугольников и выделяется среди них равными сторонами. Ромб также является частным случаем параллелограмма если у последнего все стороны равны AB=BC=CD=AD. Ниже приведен рисунок на котором изображен ромб.
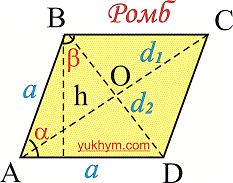
Свойства ромба
Поскольку ромб занимает некоторую часть параллелограммов то свойства в них будут похожими.
- Противоположные углы ромба как и параллелограмма равны.
- Сумма углов ромба прилегающих к одной стороне равна 180°.
- Диагонали ромба пересекаются под углом 90 градусов.
- Диагонали ромба являются одновременно биссектрисами его углов.
- Диагонали ромба в точке пересечения делятся пополам.
Признаки ромба
Все признаки ромба вытекают из его свойств и помогают различать его среди четырехугольников, прямоугольников, параллелограммов.
- Параллелограмм у которого диагонали пересекаются под прямым углом является ромбом.
- Параллелограмм у которого диагонали является биссектрисами является ромбом.
- Параллелограмм с равными сторонами является ромбом.
- Четырехугольник у которого все стороны равны является ромбом.
- Четырехугольник у которого диагонали является биссектрисами углов и пересекаются под прямым углом является ромбом.
- Параллелограмм с одинаковыми высотами является ромбом.
Формула периметра ромба
Периметр по определению равен сумме всех сторон. Поскольку в ромба все стороны равны то его периметр вычисляем по формуле
P=4a.
Периметр вычисляется в единицах длины.
Радиус окружности вписанной в ромб
Одними из распространенных задач при изучении ромба является нахождение радиуса или диаметра вписанной окружности. На рисунке изображенном ниже приведены одни из распространенных формул радиуса вписанной окружности в ромб.
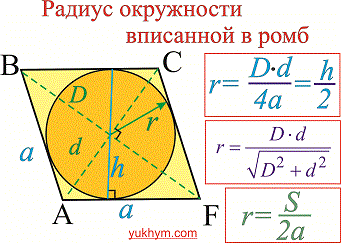
Первая формула показывает что радиус окружности вписанной в ромб равен произведению диагоналей разделенному на сумму всех сторон (4а).
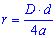
Другая формула показывает что радиус окружности вписанной в ромб равен половине высоты ромба
r=h/2.
Вторая формула на рисунке является модификацией первой и применяется при исчислении радиуса окружности вписанной в ромб когда известны диагонали ромба, то есть неизвестные стороны.
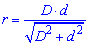
Третья формула радиуса вписанной окружности фактически находит половину высоты малого треугольника, который образуется пересечением диагоналей.
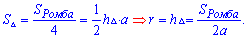
Среди менее популярных формул для вычисления радиуса окружности вписанной в ромб можно еще привести такие
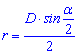
здесь D – диагональ ромба, alpha – угол который рассекает диагональ.
Если известна площадь (S) ромба и величина острого угла (alpha) то для вычисления радиуса вписанной окружности нужно найти квадратный корень из четверти произведения площади на синус острого угла:
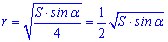
Из приведенных формул Вы без проблем найдете радиус вписанной в ромб окружности, если в условиях примера будут необходимый набор данных.
Формула площади ромба
Формул для вычисления площади приведены на рисунке.
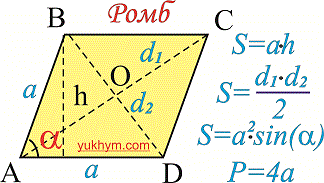
Простейшая выводится как сумма площадей двух треугольников на которые разделяет ромб его диагональ.
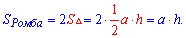
Вторая формула площади применяется к задачам в которых известны диагонали ромба. Тогда площадь ромба равна половине произведению диагоналей
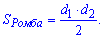
Она достаточно проста для того чтобы запомнить, а также - для вычислений.
Третья формула площади имеет смысл когда известен угол между сторонами. Согласно ей площадь ромба равна произведению квадрата стороны на синус угла. Острый он или нет значения не имеет поскольку синус обоих углов принимает одинаковое значение.
Периметр ромба
Периметр ромба равен сумме всех его сторон. Учитывая то что они все равны периметр принимает значение
P=4a.
И в завершение запомните что периметр измеряется в единицах длины, а площадь в квадратных единицах. Теперь Вы знаете как найти площадь и периметр ромба, поэтому пользуйтесь приведенным формулам при решении задач.
Посмотреть материалы:


