Далі будуть розв'язані задачі на трапеції в яких діагоналі перпендикулярні між собою. Пам'ятайте, що не тільки у рівнобічних трапецій діагоналі взаємоперпендикулярні. Далі наведемо популярні властивості рівнобічних трапецій, які Ви часто зможете застосувати на практиці.
Властивість 1. Якщо в рівнобічній трапеції діагонали перпендикулярні, то висота трапеції рівна півсумі основ.
Доведення: Проведено через точку C пряму CF, паралельну BD і продовжимо пряму AD до перетину з CF.
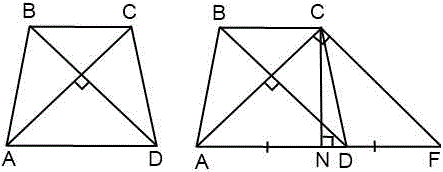
Чотирикутник BCFD - паралелограм (BC//DF за означенням основ трапеції, BD//CF з побудови). Звідси слідує
CF=BD, DF=BC, AF=AD+BC.
Трикутник ACF прямокутний (якщо пряма перпендикулярна одній з двох паралельних прямих, то вона перпендикулярна і до другої прямій). Оскільки в рівнобічної трапеції діагоналі рівні, а CF = BD, то CF = AC, тобто трикутник ACF - рівнобедрений з основою AF.
Отже, його висота CN є також медіаною.
А так як медіана прямокутного трикутника, проведена до гіпотенузи, дорівнює її половині, то
CN =(AD + BC)/2
що в загальному вигляді можна записати:
h=(a+b)/2,
де h - висота трапеції, a,b - основи.
Властивість 2. Якщо в рівнобедреної трапеції діагоналі перпендикулярні, то її висота дорівнює середній лінії.
h=m=(a+b)/2.
Властивість 3 Якщо в рівнобічної трапеції діагоналі перпендикулярні, то площа трапеції дорівнює квадрату висоти трапеції (або квадрату напівсуми підстав, або квадрату середньої лінії).
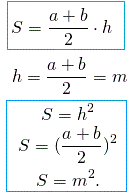
Властивість 4. Якщо в рівнобічної трапеції діагоналі перпендикулярні, то квадрат діагоналі дорівнює половині квадрата суми основ, а також подвоєному квадрату висоти і подвоєному квадрату середньої лінії.
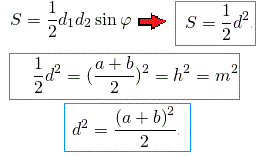
Задачі на взаємоперпендикулярні діагоналі трапецій
Приклад 1. Діагоналі трапеції перпендікулярні і рівні 6 та 8 см. Знайти середню лінію трапеції.
Розв'язування: Виконаємо допоміжну побудову.
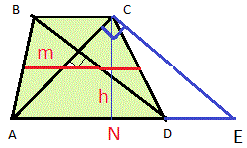
За умовою AC⊥BD, AC=6 см, BD = 8 см, AD- нижня основа, ВС-верхнє. Проведемо СЕ параллельно ВD. Продовжимо сторону АD до перетину з СE в точці E.
Трикутник АСE - прямокутний
АС=6, СК=ВD=8.
За теоремою Піфагора:
АE= √(AC² + CE²)=√(64+36)=√100=10
АE=АD+DE=АD+ВС=10 сума основ.
Середня лінія дорівнює півсумі основ трапеції
m=AE/2=5 см.
Відповідь: 5 см.
Приклад 2. Діагоналі рівнобічної трапеції взаємно перпендикулярні. Знайдіть площу трапеції, якщо її висота 7 см.
Розв'язування: За 3 властивістю, півсума основ рівнобічної трапеції рівна висоті
(a+b)/2=h=7 см.
Обчислюємо площу
S=h*(a+b)/2=h^2=7^2=49 см2.
Відповідь: 49 см2.
Приклад 3. Діагоналі трапеції взаємно перпендикулярні і дорівнюють 12 і 16 см.Знайти висоту трапеції.
Розв'язування: Використаємо рисунок 1 задачі. Така добудова використовується доволі часто, тому запам'ятайте, що вона дає в обчисленнях.

Нехай AC=12 см, BD=16 см.
BD||CE. BD=CE, ∠ACE=900.
Трикутник ACE прямокутний, тому за теоремою Піфагора
AE^2=AC^2+CE^2,
AE2=122+162=400=202 ,
AE=20.
Висоту трапеції знайдемо з формул площі прямокутного трикутника ACE.
З однієї сторони площа рівна половині добутку катетів
S=AC*CE/2,
з іншої – половині добутку висоти на основу трикутника
S=h*AE/2.
Виводимо формулу висоти та обчислюємо
h*AE/2=AC*CE/2,
h=AC*CE/AE,
h=12*16/20=9,6 см.
Відповідь: 9,6 см.
Приклад 4. Діагоналі трапеції взаємно перпендикулярні, одна з них дорівнює 48 см, а середня лінія трапеції- 25 см. Знайдіть висоту трапеції.
Розв'язування: Використовуємо це й же малюнок і подібні міркування.

AC=48 см, m=25 см.
Площа трикутника ACE рівна півдобутку діагоналей. З іншої сторони вона рівна півдобутку основи на висоту. Оскільки середня лінія трапеції ABCD одночасно рівна середній лінії трикутника ACE, то основа трикутника рівна подвоєній середній лінії (BD||CE, DE=BC).
За теоремою Піфагора знаходимо другу діагональ трапеції
AE=2m=2*25=50 см
CE=√(AE2-AC2) =√(502-482)=√196=14 см.
В попередній задачі вивели формулу, згідно з якої висота рівна відношенню добутку діагоналей до подвоєної середньої лінії
h=AC*CE/AE=48*14/50=13,44 см.
Відповідь: 13,44 см.
Приклад 5. Діагоналі трапеції взаємно перпендикулярні і дорівнюють 5 і 12 см. Знайти висоту трапеції та площу.
Розв'язування: Допоміжну побудову до трапеції запамятайте, адже на ній обчислюють багато завдань.

AC=5, BD=12. BD||CE, BD=CE.
За теоремою піфагора обчислюємо гіпотенузу трикутника ACE
АE= √(AC² + CE²)=√(5^2+12^2)=√(25+144)=√169=13.
Далі знаходимо висоту трапеції за формулою
h=AC*CE/AE=5*12/13=60/13≈4,6 см.
Середня лінія трапеції рівна половині АE, оскільки DE=BC.
Обчислюємо площу трапеції
SABCD=m*h=h*AE/2=60/13*13/2=30 см2.
Відповідь: 4,6 см, 30 см2.
Приклад 6. У рівнобічній трапеції діагональ є бісектрисою гострого кута. Одна з основ на 6 см більша за другу. Знайдіть середню лінію трапеції, якщо його периметр рівний 74.
Розв'язування: Нехай AC - бісектриса кута ∠A. Позначимо BC=x, тоді більша основа
AD=x+6.
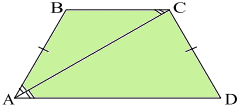
За означенням бісектриси ∠BAC=∠CAD, BC||AD, AC- січна, тому ∠BCA=∠CAD. Оскільки гострі кути в трикутнику ABC рівні, то він рівнобедрений. Звідси AB=BC=CD=x.
Складаємо рівняння на периметр
PABCD=x+x+x+x+6=74
4x=74-6=68,
x=68/4=17.
AD=x+6=17+6=23 см.
Далі знаходимо середню лініютрапеції
m=(BC+AD)/2=(17+23)/2=20 см.
Відповідь: 20 см.
Приклад 7. Діагоналі рівнобічної трапеції взаємно перпендикулярні, а середня лінія 9 см . Знайти площу трапеції
Розв'язування: У рівнобічної трапеції висота рівна середній лінії (див. властивість 2), тому площа трапеції рівна
S=m^2=9^2=81 см2.
Відповідь: 81 см2.
Якщо маєте повчальні задачі на трапеції, які допоможуть на практичних учням та стосуються теми, надсилайте їх нам. Ми їх добавимо до наведених прикладів.
Пам'ятайте, що ми постійно працюємо для Вашого успіху в освіті!


