Продовжуємо розбирати готові відповіді до посібника з підготовки до ЗНО (зараз розв'язано біля 1000 прикладів).
Сьогодні розглянемо задачі на властивості паралелограма. Завдання не надто складні і всього за кілька хвилин Ви зможете пригадати шкільний курс геометрії за 8-10 класи. Всі відповіді доповнені рисунками паралелограмів, тому пояснення та підписи Вам будуть зрозумілі.
Автори: Анатолій Капіносов, Галина Білоусова, Галина Гап'юк, Сергій Мартинюк, Лариса Олійник, Петро Ульшин, Олег Чиж
Завантажити онлайн відповіді (Посібник для підготовки до зовнішнього незалежного тестування з математики).
Зміст: Посібник містить поради щодо проходження ЗНО з математики та взірці тестових завдань. Усі задачі однієї теми розміщені в порядку складності.
Рекомендуємо всім завантажити відповіді до ЗНО та самостійно пройти теми, з якими маєте труднощі на практичних.
Тема 32. Чотирикутники
Задачі на властивості паралелограма
Тема чотирикутників містить в собі приклади на прямокутники, паралелограми, ромби трапеції. В такому порядку ми їх погрупували, щоб Ви розглядали їх окремо одні від одних.
Задача 32.1 Сума кутів паралелограма дорівнює 1300.
Знайти найбільший кут паралелограма.
Обчислення: Нехай маємо паралелограм з кутами alpha і beta.
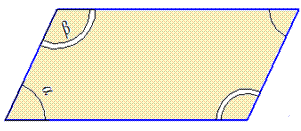
За властивістю паралелограма: протилежні кути у нього рівні, також сума сусідніх кутів дорівнює 180 градусів
(звідси робимо висновок, що тільки протилежні кути паралелограма можуть в сумі давати 130).
Тому маємо alpha+beta=180, за умовою задачі alpha+alpha=130, тобто alpha=130/2=65.
beta=180-alpha=180-65=115 – найбільший кут паралелограма.
Відповідь: 1150 – Г.
Задача 32.2 Периметр паралелограма дорівнює 84 см, а сума двох його сторін – 58 см.
Знайти меншу сторону паралелограма. 
Обчислення: Намалюємо паралелограм зі сторонами a і b.
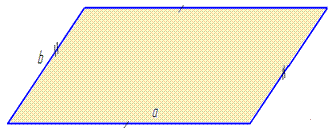
За властивістю паралелограма: протилежні сторони у нього рівні.
Оскільки периметр паралелограма – це сума всіх сторін, то маємо
2(a+b)=84, або
a+b=42.
Звідси видно, що сума сусідніх сторін НЕ може дорівнювати 58 см, тому
a+a=58, звідси a=29 см
b=42-a=42-29=13 см – менша сторона паралелограма.
Відповідь: 13см – Д.
Задача 32.3 Бісектриса гострого кута паралелограма поділяє сторону на відрізки завдовжки 7 см і 10 см, починаючи від вершини тупого кута.
Знайти периметр паралелограма.
Обчислення: Нехай маємо паралелограм ABCD, AB||DC і AD||BC, AK – бісектриса.
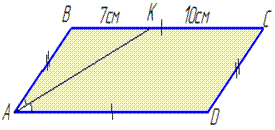
За умовою: BK=7 см, RC=10 см, тому маємо BC=BK+KC=7+10=17 см.
За властивістю паралелограма:
AD=BC=17 см.
Оскільки AK – бісектриса, то ∠BAK=∠KAD.
За ознакою паралельності прямих (AD||BC), як перетнуті січною AK, маємо ∠AKB=∠KAD.
Тому ∠BAK=∠AKB.
Звідси слідує (за теоремою), що ΔABK– рівнобедрений з основою AK і бічними сторонами AB і BK, тому (за означенням) AB=BK=7 см.
За властивістю паралелограма:
CD=AB=7 см.
Знайдемо периметр паралелограма (сума всіх його сторін):
P=AB+BC+CD+AD=2(AB+BC)=2(7+17)=48 см.
Відповідь: 48 см – А.
Задача 32.10 Сторони паралелограма дорівнюють 18 см і 30 см, а висота, яка проведена до більшої сторони, - 6 см. Знайти іншу висоту паралелограма.
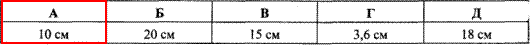
Обчислення: Виконаємо побудову паралелограма у якого AB||DC і AD||BC, CK ⊥AB, AH ⊥BC, де CK і AH – висоти паралелограма, опущені на сторони AB і BC, відповідно.
За умовою:
AB=30 см, BC=18 см, CK=6 см
Площа паралелограма дорівнює добутку сторони на висоту, проведену до неї.
Обчислимо площу паралелограма ABCD:
S[ABCD]=AB•CK=30•6=180 cм2
Але площу паралелограма можна обчислити також за формулою:
S[ABCD]=BC•AH, звідси
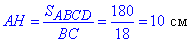
Відповідь: 10 см – А.
Задача 32.13 Висоти паралелограма дорівнюють h1 і h2, а кут між ними – alpha.
Визначити площу паралелограма.
Обчислення: Нехай маємо паралелограм ABCD, AB||CD і AD||BC, BM⊥AD, BN⊥CD, де BM і BN – висоти паралелограма, опущені на сторони AD і CD, відповідно.
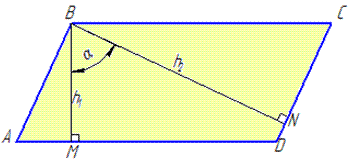
∠MBN=alpha (за умовою), тоді ∠NBC=90-alpha, оскільки BM⊥BC.
Розглянемо прямокутний трикутник BNC (∠BNC=90).
У нього ∠BNC=90-alpha, BN=h2 – прилеглий катет до ∠NBC, знайдемо гіпотенузу BC за означенням косинуса гострого кута, причому cos(90-alpha)=sin(alpha):
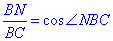, звідси
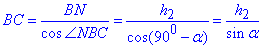
За властивістю паралелограма (протилежні сторони рівні), маємо:
AD=BC=h2/sin(alpha).
Знайдемо площу паралелограма:
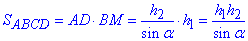
Відповідь: h1•h2/sin(alpha) – Б.
Задача 32.20 Одна з діагоналей паралелограма дорівнює d і поділяє його гострий кут на кути alpha і beta.
Визначити площу паралелограма.
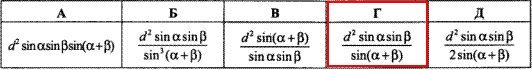
Обчислення: Записуємо дані з умови та з властивостей паралелограма AB||CD і AD||BC, AC=d, ∠BAC=alpha, ∠CAD=beta, де AC – діагональ паралелограма.
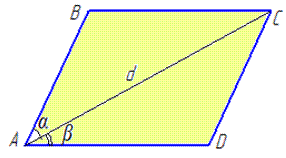
Тоді ∠A=∠BAC+∠CAD=alpha+beta, оскільки сума сусідніх кутів паралелограма 1800 (за властивістю), то
∠B=180-∠A=180-(alpha+beta).
∠ACB=∠ACD=beta як внутрішні різносторонні кути при паралельних прямих AB, CD і січній AC (за властивістю).
Розглянемо трикутник ABC, у якого AC=d і ∠BAC=alpha, ∠ABC=180-(alpha+beta).
∠ACB=beta.
За теоремою синусів знайдемо сторони AB і BC:
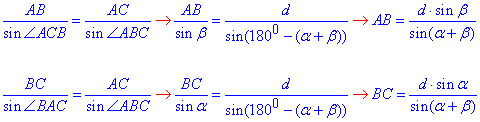
Знайдемо площу паралелограма (за двома сторонами і кутом між ними):
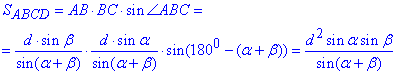
Тут була використана формула зведення для синуса гострого кута:
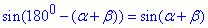
Відповідь: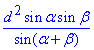 
– Г.
Задача 32.24 Периметр паралелограма більший від однієї з його сторін на 23 см і більший на 19 см від іншої його сторони.
Знайти периметр паралелограма.
Обчислення: Побудуємо паралелограм зі сторонами a см і b см.
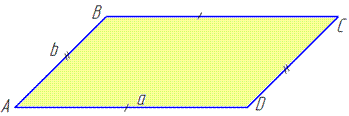
Оскільки протилежні сторони паралелограма рівні (за властивістю), то його периметр визначаємо через подвоєну суму сусідніх сторін:
P=2a+2b.
За умовою задачі, маємо:
2a+2b-a=23 (*) і
2a+2b-b=19 (**).
Отримали систему двох рівнянь з двома невідомими:
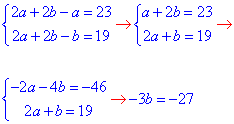
звідси b=9 і a=5.
Знаючи сторони, без проблем знаходимо периметр паралелограма за формулою:
P=2a+2b=2•5+2•9=28 см
Відповідь: 28 см – Б.
Задача 32.27 Сторони паралелограма дорівнюють 12 см і 5 см. Установити відповідність між величинами гострих кутів (1–4) паралелограмів і їх площами (А – Д).
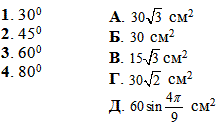
Обчислення: Нехай маємо паралелограм зі сторонами a=12 см, b=5 см і кутом між ними phi.
Запишемо формулу площі паралелограма за сторонами та кутом між ними:
S=a•b•sin(phi).
Знайдемо обчислимо площу паралелограма для заданого кута phi:
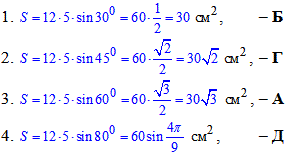
Задача 32.30 Одна з діагоналей паралелограма дорівнює 6 √6 і утворює зі стороною паралелограма кут 600.
Знайти іншу діагональ, якщо вона утворює з тією ж стороною кут 450.
Обчислення: Маємо паралелограм ABCD, AB||CD і AD||BC, AC=6 √6, ∠CAD=60, ∠BDA=45, де AC і BD – діагоналі паралелограма, які перетинаються в точці O.
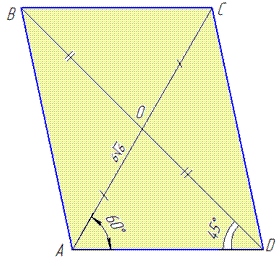
Тоді, за властивістю паралелограма
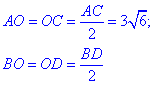
Розглянемо трикутник AOD, у якого
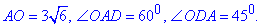
За теоремою синусів знайдемо сторону OD:
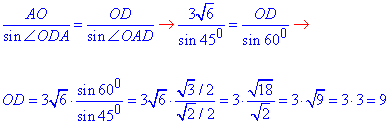
Знайдемо діагональ BD паралелограма ABCD:
оскільки BO=OD=BD/2=9, то BD=2•OD=2•9=18.
Відповідь: 18.
В наступній статті розберемо тестові задачі на ромби.
