Готові приклади на область значень, парності та непарності функцій, періодичності стануть Вам добрими помічниками в шкільній практиці та при підготовці до ЗНО тестів з математики. Сьогодні розберемо тести в яких потрібно знайти множину значень функції, або навпаки за ескізом функції знайти функцію, якій належить графік.
Розділ 22. Елементарні функції та їх властивості
Приклад 22.8 Знайти множину значень функції y=-2cos(x)+5.
Розв'язування: Будь-які функції слід аналізувати від внутрішніх вложених, до кінцевих.
Розглянемо функцію z=cos(x). Її найменше значення zmin=-1, а найбільше zmax=1 (за властивістю функції косинуса z=cos(a•x+b)).
Побудуємо графіки обох функцій
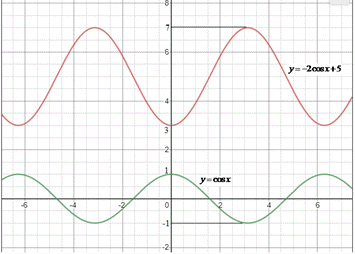
Підставивши найменше і найбільше значення функції косинус у заданий вираз, отримаємо найбільше і найменше значення заданої функції, відповідно:
ymax=-2•(-1)+5=7;
ymin=-2•1+5=3.
Запишемо множину значень заданої функції:
E(y)=[3;7].
Відповідь: [3;7] – Г.
Приклад 22.9 Знайти множину значень функції y=3cos(x+Pi/3)-2.
Розв'язування: Алгоритм обчислень аналогічний до попереднього завдання.
Розглянемо функцію z=cos(x+Pi/3).
Її найменше значення zmin=-1, а найбільше zmax=1 за властивістю функції косинуса z=cos(a•x+b).
Графіки функцій, що аналізуємо наведено на рисунку
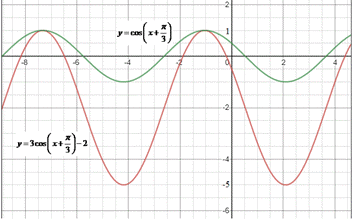
Підставивши найменше і найбільше значення функції косинус у заданий вираз, отримаємо найменше і найбільше значення заданої функції, відповідно:
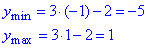
Запишемо множину значень косинуса:
E(y)=[-5;1].
Відповідь: [-5;1] – Б.
Приклад 22.10 Функція y=f(x) є спадною на проміжку (-∞;+∞). Указати правильну відповідь.
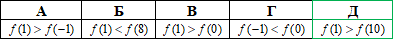
Розв'язування: Якщо функція y=f(x) є спадною на проміжку (-∞;+∞), то f(x1)>f(x2), якщо x1<x2, або f(x1)<f(x2), якщо x1>x2.
Оскільки f1<10, то f(1)>f(10).
Відповідь: f(1)>f(10) – Д.
Приклад 22.11 Дано функцію f(x)=(1-x)/(1+x). Знайти f(x+1).
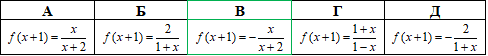
Розв'язування: У заданій функції f(x)=(1-x)/(1+x) замінимо x на вираз x+1, отримаємо
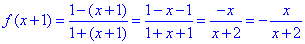
Приклад 22.32 Установити відповідність між функціями (1–4) та їхніми множинами значень (А–Д).
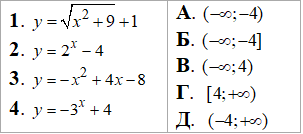
Розв'язування: Продовжуємо вивчати властивості елементарних функцій. Для наочності наведемо графіки функцій, щоб краще уявляти що досліджуємо.
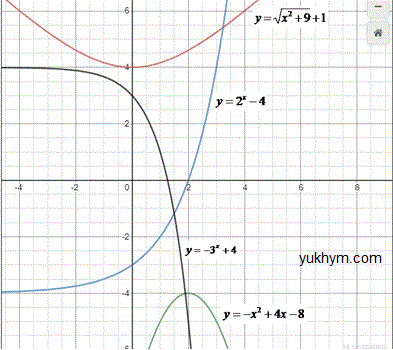
1) Коренева функція від x2+9 визначена і парна при всіх значеннях x. Функція зростає, якщо x>0 і спадає, якщо x<0 (на рис. червоний колір).
Найменше значення досягається при x=0:
ymin=√(02+9)+1=4.
Найбільшого значення функція не має, тобто прямує до плюс безмежності.
Отже, множина значень заданої функції:
E(y)=[4;+∞), що відповідає варіанту Г ЗНО тестів з математики.
2) y=2x -4.
Задана показникова функція визначена і зростає при всіх значеннях x (на рис. синій колір).
Найменше значення (при x→-∞), 2x→0 за властивістю показникової функції:
ymin→-4>.
Зверху показникова функція нічим не обмежена, тому при великих значеннях аргументу прямує до плюс нескінченності.
Множина значень заданої функції:
E(y)=(-4;+∞) Д.
3) y=-x2+4x-8
Крива y=a*x2+bx+c є рівнянням параболи з гілками вниз, a=-1<0 (на рис. зелений колір).
Найбільше значення функції у вершині параболи:
, .
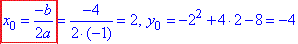Найменшого значення функція не має.
Отже, множина значень заданої функції:
E(y)=(-∞;-4] Б
4. y=-3x+4
Лінійна функція визначена і спадає при всіх значеннях x (на рис. чорний колір).
Найбільше значення (при x→-∞, -3x→0 за властивістю показникової функції):
ymax→4.
Найменшого значення функція не має.
Отже, множина значень заданої функції:
E(y)=(-∞;4). Таку відповідь містить варіант В тестів.
Приклад 22.33 Установити відповідність між функціями (1–4) та їхніми множинами значень (А–Д).
Розв'язування: Усі задані функції є оберненими тригонометричними, тому перш ніж братися за них повторіть їх властивості, хоча б множини значень та області визначення.
Функції не складні тому тут багато пояснювати не будемо, лише наведемо схему обчислень:
1. y=2arcsin(x),
,
Множина значень арксинуса y=2arcsin(x) рівна:
E(y)=[-π;π], це відповідає варіанту Б тестів.
2. y=2arccos(x),
0≤arccos(x) ≤π
0≤2arccos(x) ≤2π
Множина значень арккосинуса y=2arccos(x) рівна:
E(y)=[0;2π] – Д.
3. y=2arctg(x),
,
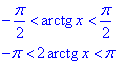Множина значень арктангенса y=2arctg(x):
E(y)=(-π;π) А.
4. y=2arcctg(x),
0<arcctg(x)<π
0<2arcctg(x)<2π
Множина значень арккотангенса y=2arcctg(x) рівна:
E(y)=(0;2π). Г.
Приклад 22.31 Кожній точці (1–4) поставити у відповідність функцію (А–Д), графіку якої належить ця точка.
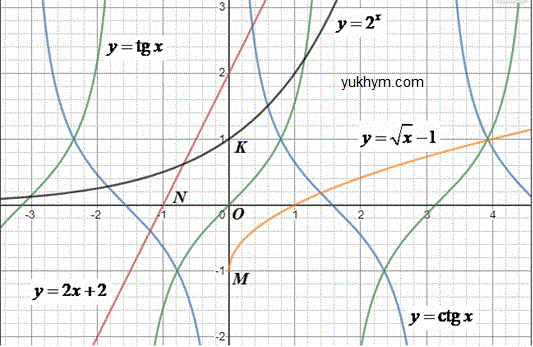
Розв'язування:
1. Через початок координат (0;0) проходить графік котангенса, графік якого на рисунку показаний зеленим кольором. 1 - В.
2. Точка M(0;-1) належить графіку кореневої функції y=√x-1, оскільки √0-1=-1.
На рисунку графік показаний жовтим кольором. 2 - Г.
3. Точка N(-1;0) належить графіку лінійної функції y=2x+2, оскільки 2•(-1)+2=0.
На рисунку графік показаний червоним кольором. 3 - А.
4. Точка K(0,1) належить графіку функції y=2x, оскільки 2·0=1.
На рисунку графік показаний чорним кольором. 4 - Д.
Приклад 22.36 Дано лінійну функцію y=ax+b.
Установити відповідність між знаками коефіцієнтів a й b (1–4) та ескізами графіків (А–Д).
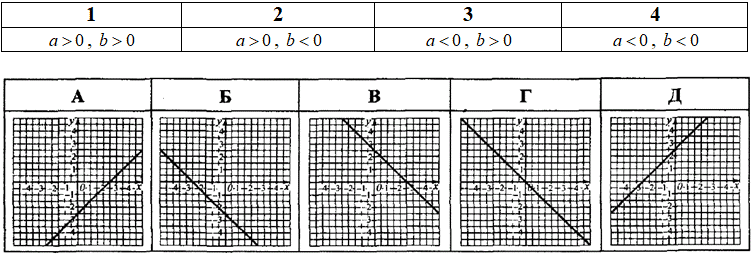
Розв'язування: Детальне пояснення як аналізувати графіки лінійної "функції - прямої" дивись у 22.16.
a>0, якщо функція зростає (або якщо пряма утворює гострий кут з додатним напрямком осі Ox) і
a<0, якщо функція спадає (або якщо пряма утворює тупий кут з додатним напрямком осі Ox).
Параметр b вказує на ординату перетину прямої y=ax+b з віссю Oy.
Отже, враховуючи вище наведені властивості прямої y=ax+b, отримаємо
1 - Д. 2 - А. 3 - В. 4 - Б.
Приклад 22.40 Установити відповідність між функціями (1–4) та ескізами їх графіків (А–Д).
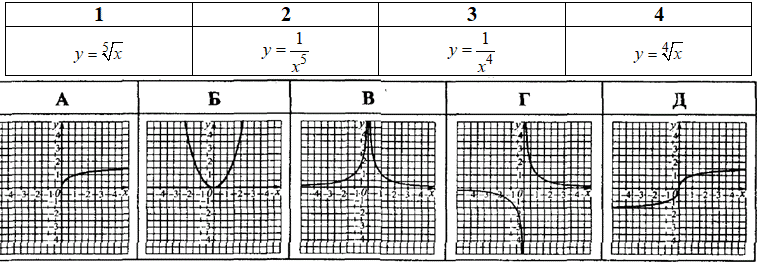
Розв'язування: 1. коренева функція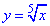 
визначена і зростаюча для всіх x, непарна (симетрична відносно початку координат), тому серед наведених ескізів їй відповідає варіант – Д.
2. функція y=1/x5 - визначена для всіх x≠0 і спадна, непарна (симетрична відносно початку координат), на ескізі їй відповідає варіант 2– Г.
3. функція y=1/x4 - визначена для всіх x≠0, парна (симетрична відносно осі ординат), зростає при x<0 і спадає при, x>0, її відповідає 3 – В.
4. функція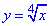 
- визначена і зростаюча для всіх x≥0, на ескізі варант А.
Далі наведені розв'язки ЗНО тестів на парність та непарність функцій, періодичність, аналіз складних та обернених функцій. Ще ряд завдань в яких за ескізом параболи y=ax2+bx+c потрібно знайти коефіцієнти a,b,c ми згрупували і об'єднали в статтю, яку Ви можете знайти в наступних уроках.
