Під випробуванням (експериментом)розуміють деяку сукупність умов, за яких спостерігається те або інакше явище, фіксується той або інший результат. Дослід може проводитися багаторазово в подібних (незмінних основних) умовах, проте ряд другорядних умов та факторів, які неможливо проконтролювати змінюється від випробування до випробування та приводить до різних результатів наслідків експерименту.
Випадковою подією (подією) називається будь-який факт, який в результаті експерименту може відбутися чи не відбутися. Випадкові події позначають великими латинськими буквами A, B, C.
Ймовірністю подіїназивається чисельна міра свободи впевненості в появі даної події внаслідок нового випробування.
Імовірність події A позначається як P(A).
Вірогідною (достовірною) називається подія U, яка внаслідок випробування неодмінно повинна статися. Для достовірної події ймовірність рівна одиниці P(U)=1.
Неможливою називається подія  , яка внаслідок досвіду не може відбутися. Для неможливої події ймовірність рівна нулю
, яка внаслідок досвіду не може відбутися. Для неможливої події ймовірність рівна нулю 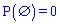 .
.
Ймовірність будь-якої випадкової події Aприймає значення між нулем і одиницею
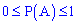 .
.
Повною групою подій називаються декілька таких подій, що внаслідок випробування неодмінно повинна статися хоча би одна із них.
Декілька подій у досліді називаються несумісними, якщо ніякі два з них не можуть з'явитися одночасно.
Декілька подій у випробуванні називаються рівноможливими якщо вони мають рівні шанси появи в результаті випробування. Прикладами рівноможливих подій можна відзначити появу:герба або цифри при одному підкиданні монети; парного і непарного числа очок при одному підкиданні грального кубика і т.д.
Якщо наслідки випробування утворять повну групу несумісних рівноможливих подій, то вони називаються випадками.
Множина всіх результатів експерименту, що розглядається називається простором елементарних подій.
Наслідок (випадок) називається сприятливим події A, якщо він спричиняє до обов'язкової появи подіі A.
КЛАСИЧНЕ ВИЗНАЧЕННЯ ЙМОВІРНОСТІ
Якщо результати випробування зводяться до схеми випадків, то ймовірність появи події A обчислюється за формулою
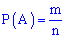
Де n – загальне число випадків; m – число випадків, сприятливих події A.
Наведене співвідношення є класичною формулою обчислення ймовірності подій.
Прості задачі теорії ймовірностей
Приклад 1. В цеху по виготовленню м'ячів для гольфу в одній коробці було 77 правильної форми мячів та 23 мячі з дефектами в іншій. Мячі зсипали в одну коробку. Яка ймовірність того, що навмання витягнутий м'яч буде бракованим ?
Розв'язанняЗагальне число рівноможливих подій рівне кількості всіх мячів
n=77+23=100.
Число сприятливих події, яка полягає у витягненні бракованого мяча рівне їх кількості
m=23.
За формулою ймовірності знаходимо
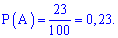
Ймовіпність витягнути бракований м'яч рівна 0,23.
Приклад 2. На столі викладені кубики з номерами від одиниці до дев'яти. Учень навмання витягує один кубик. Яка ймовірність того, що:
A- число з кубика ділиться на 3?
B - число ділиться на 2?
Розв'язанняЗагальне число випадкових подій рівне кількості кубиків n=9.
Число події сприятливих A можна зобразити у вигляді множини A={3;6;9}, для B множина сприятливих подій буде наступною B={2; 4; 6; 8}. На основі цього число m приймає значення m=3 та m=4 для першої та другої події відповідно. Ймовірність їх появи визначаємо за формулами
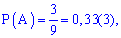
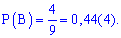
Ось з таких простих розахунків розпочинається теорія ймовірності. Схеми та загальні основи знаходження ймовірності використовуються в набагато складніших формулах, про них піде мова в наступних уроках.
Приклад 3. В групі 17 хлопців та 13 дівчат. Викладачеві потрібно викликати когось для перевірки виконання домашніх завдань. Яка ймовірність того, що до дошки вийде дівчина?
Розв'язанняЗагальне число рівносильних подій рівне кількості учнів
n=17+13=30.
Кількість дівчат m=13.
На основі цьоо шукана ймовірність рівна частці
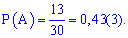
тобто 0, 43(3).
Приклад 4. Кидають два гральні кубики і записують кількості очок , які випали на їх гранях. Знайти ймовірність того, що із записаних цифр можна скласти: а) два різні двоцифрові числа;
б) лише одне парне двоцифрове число.
Обчислення: Кубик має 6 граней з кількістю точок на гранях 1,2,3,4,5,6.
а) Випишемо можливі два різні двоцифрові числа
24,42,46,64,26,62.
Їх небагато, а кількість рівна n1=6.
б) одне парне двоцифрове число
22,44,66.
n2=3.
Кількість можливих варіантів при двох кидках кубика рівна
N=6•6=36;
Ймовірності визначаємо, як частку сприятливих способів отримати потрібні очки на гранях до все можливих, тому:
p1=6/36=1/6.
p2=3/36=1/12.
Відповідь: 1/6, 1/12.
Теорія ймовірностей є важливою для практики наукою. На ній побудовані всі лотереї та азартні ігри, ставки за депозитами і кредитами, прийняття рішень на біржах акцій та валют також не обходиться без неї. При цьому застосовуються достатньо складні для розуміння процеси прийняття рішень та аналізу подій, однак теорія ймовірностей присутня всюди.
]]>При великому числі можливих наслідків випробування способи прямого перебору можливих варіантів малоефективні. На допомогу приходять комбінаторні методи, в основі яких лежать два настутних правила.
ПРАВИЛО ДОДАВАННЯ
Якщо дві взаємовиключні події можуть бути виконані відповідно k та m способами, тоді якусь одну з цих подій можна виконати k+m способами.
Приклад 1. З міста А в місто В можна добратися 12 потягами, 3 літаками, 23 автобусами. Скількома способами можна добратися з міста А у місто В?
Розв'язання. Проїзд з А у В на потягу, літаку або автобусом є подіями, які не можуть виконуватися одночасно однією людиною (взаємовиключними), тому загальну кількість маршрутів можна обчислити сумуванням способів пересування
N=12+3+23=38.
В цьому і полягає правило додавання.
ПРАВИЛО МНОЖЕННЯ
Нехай дві виконувані одна за одною дії можуть бути здійснені відповідно k та m способами. Тоді обидві вони можуть бути виконані k*m способами.
Приклад 2. У турнірі беруть участь 8 команд з хокею. Скільки існує способів розподілити перше, друге та третє місця?
Розв'язання. Відповідно до умови аналіз призових місць має бути наступним:
перше місце займе одна з 8 команд, друге – одна з 7, третє – одна з 6, оскільки кожна з них не може претендувати одночасно на два призових місця. Тому таких способів буде
N=8*7*6=336
Обидва правила узагальнюються на випадок будь-якої скінченної кількості дій.
У комбінаториці розрізняють три види різних з'єднань (комбінацій) елементів фіксованої множини: перестановки, розміщення, сполучення. Нижче будуть дані їх означення з позначеннями, які найбільшвживані.
Перестановками з m елементів називаються такі їх сукупності, що відрізняються одна від іншої тільки порядком входження елементів. Їх позначають P(m) та визначають за формулою
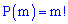
 - факторіал числа m, визначається за правилом
- факторіал числа m, визначається за правилом 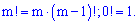
Приклад 3.Скількома способами можна в садочку поставити групу з 15 дітей в ряд?
Розв'язання. На перше місце є можливість поставити когось із 15 дітей, на друге одного з 14 і т.д. Загальна кількість рівна 15 факторіал
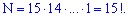
Переглянути приклади на перестановки.
Розміщеннями з n елементів по m називаються такі сукупності m елементів, що відрізняються одна від іншої принаймні одним елементом або порядком їх входження (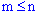 ):
):
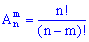
Фомула розміщень не надто складна і доволі часто Ви будете нею ористуватися на практиці, тому рекомендуємо її вивчити.
Приклад 4. Скільки різних трицифрових чисел можна скласти за допомогою цифр від 1 до 9?
Розв'язання Загальна кількість чисел обчислюється за формулою розміщень
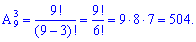
Отримана відповідь Вам і зрозуміла і тривіальна. Переглянути задачі на розміщення.
Сполученнями з n елементів по m називаються такі сукупності m елементів, що відрізняються одна від іншої принаймні одним елементом (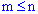 ) :
) :
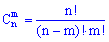
З формули сполучень бачимо, що вони приймають ще менше значення ніж розміщення. З наступного завдання Ви зрозумієте де використовують розміщення.
Приклад 5. Скількома способами можна вибрати три цифри з дев'яти 1, 2, 3,...,9?
Розв'язання. Кількість усіх можливих способів визначаємо з формули
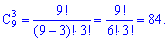
Зверніть увагу на приклади комбінацій (сполучень).
Приклад 6. Студент знає відповіді на 30 із 40 питань програми. На екзамені він отримує білет у якого 10 навмання вибраних питань програми. Яка ймовірність того, що він складе іспит з оцінкою «відмінно», якщо для цього потрібно відповісти не менше, ніж на 9 питань білета?
Розв'язання: Оскільки порядок входження питань в білет не важливий, а тільки має значення чи знає студент відповідь на питання, то слід застосовувати формулу сполучень. Кількість всеможливих способів сформувати білети з 10 питань серед 40 рівна
n=С4010=40!/(10!•30!)=847660528.
Відповісти потрібно на 9 з 10 або всі 10 питань.
1) 9 з 10 означає вибрати 9 питань з 30 на які знає відповіді і 1 з (40-30)=10, на які не знає відповіді, тобто кількість рівна
m1=С309•С101=30!/(9!•21!)•10=143071500.
2) 10 питань в білеті, на які стент знає відповіді з 30 доступних можна сформувати С3010 способами:
m2=С3010=30!/(10!•20!)=30045015.
За правилом додавання ймовірностей кількість способів сформувати білети де студент знає відповіді не менше ніж на 9 питань з 10 рівна:
m=m1+m2=173116515.
Обчислимо ймовірність здати на відмінно екзамен
p=m/n=0,204.
Приклад 7. З колоди, в якій 36 карт, навмання вибирають 4 карти. Знайти ймовірність того, що серед них буде хоча б три тузи.
Розв'язання: З умови бачимо, що порядок входження тузів в набір з 4 карт нас не цікавить, тобто не важливо чи ми витягнемо туза першим чи останнім.
В такій ситуації слід застосовувати формулу комбінацій Сnk.
Кількість способів вибрати 4 різні карти з 36 рівна
N=С364=36!/(4!•32!)=58905.
Для любителів обчислювати в пакеті меймл за комбінації відповідає binomial(N,m):
N:=binomial(36,4)=58905.
Умова, що буде хоча б три тузи означає або 3 «або» 4 тузи.
На мові ймовірностей «або» означає додавання:
Кількість способів вибрати три тузи з 4 і ще одну карту з решти колоди (36-4)=32 рівна добутку комбінацій
m1=С43•С321=4•32=128.
4 з 4 тузів можна вибрати єдиним способом, тому
m2=C44=1.
За означенням класичної ймовірності обчислюємо частку сприятливих подій до все можливих, тому
p=(m1+m2)/N=129/58905≈0,00219.
Приклад 8. З одинадцяти букв азбуки складено заголовок української казки «КОТИГОРОШОК». Дитина, яка не вміє читати, розсипала букви, а потім зібрала в довільному порядку. Знайти ймовірність того, що вона збере слово «КОТИГОРОШОК».
Розв'язання. На здоровий глузд виглядає, що така ймовірність рівна нулю, ніяка дитина такого довгого слова не складе.Проте в теорії ймовірностей є своя дума з цього приводу і вона поягає в насупному:
з одинадцяти букв можна скласти різні буквосполучення, що відрізняються між собою тільки порядком букв, тому число всіх можливих перестановок рівна 11 факторіа
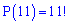
Однак букви «К» і «О» можуть займати одну з чотирьох , та одну з двох позицій відповідно, їх можна переставляти. Тому число сприятливих подій рівне
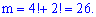
Шукана ймовірність прийме значення
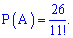
Дане число Вам нічого не говорить, бо Ви не бачите нулів після коми. Запишемо ймовірність десятковим значенням
P(A)=0,00000065...
Це означає, що лише 65 дітей зі ста мільйонів зможуть скласти слово «КОТИГОРОШОК».
Тепер завдання для батьків, просьба вислати коментар, якщо Ваша дитина несвідоо сладе хоч якесь слово хоча би з 4 букв.
Добре розберіться з наведеними прикладами на застосування правил додавання та множення, на їх основі побудований весь наступний матеріал. Попереду ще багато нового матеріалу, тут лише самі основи теорії ймовірностей.
]]>
Все решта зводиться до правила суми, коли в умові потрібно знайти одну "або" іншу множину, та правило множення коли потрібно, щоб виконувалося "і" перше "і" друге і ... правило. Якщо наведені задачі Вам будуть важкі, то можете переглянути готові приклади комбінаторики з попередніх уроків, де більше розписані правила застосування кожної з наведених тут формул.
Комбінаторні задачі на формули перестановок, комбінацій та розміщень
Задача 1. Скількома способами можна пошити двокольоровий прапор зі смужками однакової ширини, якщо є матеріал восьми різних кольорів?
Розв'язання:Відповідь на завдання знаходять через розміщення з 8 по 2, оскільки один колір можна вибрати 8 способами, другий (8-1)=7 способами.
n=A82=8*7=56.
Задача 2. Скільки різних двоцифрових чисел можна скласти, використовуючи цифри 1, 2, 3, 4, 5, 6 якщо цифри:
1) повторюються;
2) не повторюються?
Розв'язання: Якщо цифри повторюються, то на перше місце можна поставити одну з 6, на друге також любу з 6, тому кількість двоцифрових чисел з повтореннями рівна
n=6*6=36.
2) Якщо цифри не повторюються, то на друге місце можна поставити всі цифри крім тої, що на першому місці, тому кількість рівна
n=6*5=30.
Але є задачі на цифри, які в такий спосіб не розв'язати.
Задача 3. Скільки трицифрових чисел можна скласти з цифр від 0 до 5, якщо:
1) цифри не повторюються;
2) отримане число має бути непарним;
3) число має бути кратним 5.
Розв'язання: Слід зауважити, що на перше місце не можна ставити 0, тому тут може бути одна з 5 цифр {1,2,3,4,5}. На другому місці 1 з 5 цифр, оскільки одну використали, зате добавився {0}, на третьому одна з 4.
Тому кількість різних трицифрових чисел рівна
N=5*5*4=100.
2) Якщо число непарне, то на третьому місці повинні стояти цифри 1,3,5
Тобто група має вигляд ХХ{1,3,5}, тоді на перші два місця потрібно вибрати одну з 5 цифр, включаючи 0. Тому на перше місце можна поставити 4 цифри без нуля і на друге одну з 4, включаючи 0.
Тому кількість таких цифр рівна
N1=4*4*3=48.
3) Число має бути кратним 5, тому вкінці повинно закінчуватися на 0 або на 5.
Якщо на 0, то на перші два місця потрібно ставити цифри {1,2,3,4,5}. Кількість способів це зробити рівна m1=5*4=20.
Якщо закінчується на 5, то на перше місце ставимо {1,2,3,4} без 0, на друге три з цієї групи+0, тому кількість різних чисел рівна m2=4*4=16.
Якщо маємо "або" то використовуємо комбінаторне додавання
N=m1+m2=36.
Завжди розмірковуйте, які можливі випадки, як можна розгалузити випадки. Для цього потрібно навчитися ставити правильні питання: Якщо ...?
Повірте розуміння прийде з практикою, тому більше розв'язуйте самостійно.
Задача 4. Дитині подарували набір з 10 цифр та 26 букв. Скількома способами можна скласти набір із:
1) двох букв або двох цифр;
2) двох букв і двох цифр.
Розв'язання: Дві букви з 26 можна вибрати розміщеннями з 26 по 2:
m1=A262=26!/24!=26*25=650.
Аналогічна схема вибору двох цифр з 10:
m2=A102=10!/8!=10*9=90.
1) "Або" в першій умові означає, що слід застосувати правило суми для обчислення кількості груп з 2 букв або 2 цифр:
N=m1+m2=650+90=740.
2) Кількість наборів з двох букв "і" двох цифр знаходимо за правилом добутку:
N1=m1*m2=650*90=58500.
Задача 5. На паралельних прямих а і в розміщено 10 і 7 точок відповідно. Скільки існує відрізків, що з'єднують точки прямих а і в?
Розв'язання: Нехай а1, а2, …, а10 – точки на прямій а,
в1, в2, …,в7— точки на прямій в.
Для кожної точки аі матимемо 7 відрізків, що сполучають цю точку з точками прямої в.
Кожному відрізку відповідатиме пара (аі ,вj).
За формулою комбінаторного множення кількість пар рівна
N=n·m.
Задача 6. Розклад одного дня містить 6 уроків. Визначити кількість таких розкладів при
виборі із 11 дисциплін.
Розв'язання: Для нас важливий порядок предмету в розкладі, томі якщо математика буде першим, а хімія - третім уроком, то це два різні розклади, і так для всіх 11 предметів. Тому тут не слід використовувати комбінації, тільки розміщення.
Тому кількість різних розкладів рівна:
A116=11!/(11-6)!=11*10*9*8*7*6=332640.
Задача 7. Скількома способами модна вибрати двох чергових із групи 17 чоловік?
Розв'язання: Тут неважливий порядок входження школярів в групу, а лише кількість різних груп, тому застосовуємо формулу комбінацій С з 17 по 2:
C172=17!/(17-2)!/2!=17*16/2=136.
Отже, можемо скласти 136 різних пар з двох чергових.
Задача 8.В ящику є 10 деталей. Скількома способами можна вибрати 3 деталі?
Розв'язання: Нам неважливий порядок вибору, головне щоб в наборі було три деталі. Кількість різних наборів знаходимо через комбінації з 10 по 3:
C103=10!/(10-3)!/3!=10*9*8/6=120.
Задача 9. Група з 7 осіб займає місця за круглим столом випадковим чином. Яка ймовірність того, що дві певні особи сядуть поруч?
Розв'язання: Кількість всіх можливих перестановок з 7 осіб рівна n=7!, кількість сприятливих розміщень
m=2*7*5!, тому ймовірність розсадити 7 осіб, щоб дві певні особи були поруч рівна частці:
P=m/n=2*7/(7*6)=1/3.
Задача 10. На пошті в продажу є 5 різних конвертів, 6 різних марок та 7 вітальних листівок. Скількома способами можна купити комплект, що містить конверт, марку та листівку?
Розв'язання:Відповідь отримаємо комбінаторним множенням:
n=5*6*7=210.
По другому ніяк, подумайте добре!
І таких задач безліч.
Для прикладу наступні:
1. В олімпійській збірній займаються танцями7 юнаків і 9 дівчат. Скількома способами можна вибрати одну пару для участі в олімпіаді?
2. У магазині є 5 різних ручок і 9 видів зошитів. Скількома способами можна скласти комплект з1 ручки й 1 зошита?
3. Скількома способами можна дібрати пару з однієї голосної і однієї приголосної букви у слові “ворона”?
Задача 11. Знайти кількість можливих слів, які можна утворити із букв слів "урок", "школа"(під словом будемо розуміти будь-який набір цих букв).
Розв'язання: Оскільки букви в слові "урок" не повторяються, а їх кількість рівна 4, то невідома кількість рівна перестановкам з 4 букв P4:
P4=4!=4*3*2=24
"Школа" містить 5 букв без повторень, тому кількість перестановок з 5 букв рівна P5
P5=5!=5*4*3*2=120
Задача 12. Знайти кількість можливих слів, які можна скласти із букв слів "ГІПОПОТАМ", "ВЕСЕЛКА", "АНАНАС".
Розв'язання: Оскільки букви в словах повторяються, то скористаємося формулою перестановок з повтореннями.
"ГІПОПОТАМ" містить 9 букв, з яких "П" та "О" зустрічаються двічі, тому кількість різних перестановок рівна:
P9(2,2,1,..,1)=9!/(2!*2!)=90720.
"ВЕСЕЛКА" містить 7 букв, дві з яких "Е", тому кількість різних перестановок рівна
P7(2,1,1,1,1,1)=7!/2!=2520.
Слово "АНАНАС" має з букви "А", всього 6 букв. Кількість різних наборів букв з 6 рівна:
P6(3,1,1,1)=6!/3!=120.
Задача 13. Скільки різних слів можна утворити переставляючи букви слів "МАТЕМАТИКА", "КОЛОСОК", "МІССІСІПІі".
Розв'язання: Слово "МАТЕМАТИКА" має 10 букв, три "А" та по дві "М", "Т".
Тому використовуємо формулу перестановок з повтореннями
P10(3,2,2,1,..)=10!/3!/(2!)^2=151200.
"КОЛОСОК" має 7 букв, три "О" та дві "К", тому кількість перестановок за аналогічним алгоритмом рівна
P7(3,2,1,11)=7!/(3!*2!)=420.
"Міссісіпі" має 9 букв, з яких "і" повторюється 4 рази, "с" - 3 рази.
Тому перестановками можна скласти
P9(4,3,1,1)=9!/(4!*3!)=2520.
Задача 14. Скільки різних "слів" можна утворити переставляючи букви слова "ВЕГЕТЕРІАНЕЦЬ", щоби букви "РІА" стояли поруч.
Розв'язання: Слово "МАТЕМАТИКА" має 10 букв, три "А" та по дві "М", "Т".
Тому використовуємо формулу перестановок з повтореннями
P10(3,2,2,1,..)=10!/3!/(2!)^2=151200.
"КОЛОСОК" має 7 букв, три "О" та дві "К", тому кількість перестановок за аналогічним алгоритмом рівна
P7(3,2,1,11)=7!/(3!*2!)=420.
Задача 15. Скількома способами можна переставити букви в слові «ОБОРОНОЗДАТНІСТЬ», щоб дві букви «о» не стояли поряд?
Розв'язання: Досить непростий приклад в плані розв'язку, тому уважно аналізуйте алгоритм отримання відповіді.
Слово містить 16 букв, з яких 4 "О", по дві "Н" та "Т".
План такий: знайти кількість різних перестановок слова без букви "О", тобто
"БРНЗДАТНІСТЬ", це 12 букв, дві "Н" та "Т"
Далі кількість способів розставити між ними по одній О, щоб їх було 4.
Перша кількість способів рівна перестановкам з повтореннями
m1=P12(2,2,1,..)=12!/(2!*2!)=119750400.
Далі букву "О" можна поставити між 12 буквами на (12-1)=11 місцях + перед ними + після них, тому є 11+1+1=13 варіантів для 4 "О", а кількість способів це зробити рівна комбінаціям
m2= C134=13!/9!/4!=715.
Відповіддю буде добуток знайдених значень:
N=m1*m2=85621536000.
Ось Вам можливий приклад одночасно на перестановки та комбінації.
Задача 16. Скільки способів розставити 10 різних книг на 2 полках порівну?
Розв'язання: Всім зрозуміло, що потрібно розставити по 5 книг на полку, яле виникає питання: Як, скількома способами?
Так як книжки різні, то порядок розміщення на полиці має значення, тому використовуємо формулу розміщень без повторень
m1=A105=10!/5!
Другу полку заповнюємо за формулою перестановок, оскільки всі 5 книг потрібно по різному розміщувати
m2=P5=5!
На двох полках означає і там, і там, тому значення перемножуємо:
n=m1*m2=10!
Задача 17. Скількома способами переноситься слово опеньки
Розв'язання: Будьте готові до будь-яких задач, логічних і не зовсім. Хтось схоче подробити дане слово і шукати факторіали, але відповідь проста:
"Опень-ки"
і других варіантів немає, бо це правило мови, що корінь не розриваємо ...
Тому деколи керуйтеся здоровим глуздом, а не всім, що Вас вчили.
Знайти ймовірність події
Задача 18. Монету підкидують три рази. Знайти ймовірності того що:
1) Герб випаде один раз;
2) Копійка не випаде ні разу;
3) Випаде і герб і копійка;
4) Герб випаде більше раз ніж копійка
Розв'язання: В задачах де мало варіантів, доцільно виписувати всі можливі події, щоб розуміти як обчислювати. При підкиданні монети тричі можливі наступні 6 варіантів:
{ГГГ; ГГК; ГКГ; КГГ; ГКК; КГК; ККГ; ККК}
Далі серед них вибираємо ті,які сприяють нашим умовам:
1) Є всього три випадки, що герб випаде один раз серед 6 усіх
{ГКК; КГК; ККГ}
тому ймовірність рівна
P=m/n=3/8.
2) Копійка не випаде ні разу означає тричі випаде герб {ГГГ}, тому ймовірність такої події
P1=m1/n=1/8.
3) Випишемо з нашої множини всі випадки коли випаде і герб і копійка:
{ГГК; ГКГ; КГГ; ГКК; КГК; ККГ}.
Це всі події окрім тричі випаде герб та тричі копійка, тому їх кількість рівна
P2=m2/n=6/8=3/4.
4) Герб випаде більше раз ніж копійка означає, що або два або три рази. Дехто не враховує останнього варіанту, бо тоді копійка не випадає жодного разу, тобто 0 раз, але 3>0, що відповідає умові.
Випишемо всі випадки:
{ГГГ; ГГК; ГКГ; КГГ}
та знайдемо імовірність події
P3=m3/n=4/8=1/2.
Задача 19. Імовірність того, що завтра піде дощ рівна 0,2, а ймовірність того, що піде сніг становить 0,4. Яка ймовірність, що завтра не буде опадів?
Розв'язання: Обчислимо від протилежної події.
Повна ймовірність рівна одиниці.
Щоб знайти ймовірність, що опадів не буде від повної ймовірності віднімемо ймовірності опадів
P=1-p1-p2=1-0,2-0,4=0,4
Розглянемо ще кілька задач, що мають відношення до грального бізнесу: підкидання костей та роздача карт в покері.
Задача 20.Гральний кубик підкидають тричі. Скільки різних послідовностей чисел можна при цьому отримати?
Розв'язання:На гранях маємо цифри від 1 до 6. Тому на першому місці може бути одна з 6 цифр. На другому одна з (6-1)=5 цифр, одна вже на першому місці і на останньому 1 з 4.
Кількість послідовностей рівна добутку можливих комбінацій цифр:
N=6*5*4=120.
Задача 21. Кидають гральний кубик два рази. Скільки може бути випадків, при яких цифра, що випаде при першому киданні, відрізняється від цифри, що випаде при другому киданні? Скільки випадків, що цифри однакові?
Розв'язання: При першому киданні може випасти від 1 до 6, тобто 6 різних значень. Щоб друга цифра була іншою є всього 5 граней, що відрізняються,
тому кількість таких випадків рівна:
N=6*5=30.
Задача 22. Гральний кубик кидають тричі. Знайти ймовірність, що шістка випаде один раз.
Розв'язання:Шістка може випасти першою, другою, або третьою. Решту разів випадуть грані, що не містять 6, їх 5.
Тому імовірність такої події рівна
p=3*1/6*5/6*5/6 =25/72≈0,347.
Задача 23. Яка ймовірність, що при киданні грального кубика двічі, обидва рази випаде парна кількість очок..
Розв'язання:До парних належать 2, 4, 6 три значення з 6.
Тому ймовірність, що випадуть парні значення рівна:
p=3/6*3/6=1/4=0,25.
Задача 24. Яка ймовірність, витягнути дві десятки з колоди, що має 24 карти
Розв'язання: Всі знають, що в колоді є по 4 карти кожної масті. Тому потрібно знайти кількість способів витягнути 2 десятки з 4 і розділити на кількість способів вибрати 2 карти з 24. Все це знаходимо через формулу комбінацій.
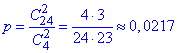
Задача 25. З колоди, що містить 36 карт (у колоді 4 тузи), виймають 5 карт. Знайти ймовірність, що серед цих карт буде хоча б один туз?
Розв'язання: Ми вже знаємо, що вибрати 5 карт з 36 можна С з 36 по 5 способами.
Далі подія - вибрати хоча б один туз означає, що або 1 або 2 або 3 або 4. Це 4 формули комбінацій, щоб їх не знаходити краще від повної ймовірності віднімемо ймовірність, що серед цих карт не буде жодного туза.
А кількість способів це зробити рівна С з (36-4 тузи)=32 по 5.
Обчислюємо ймовірність
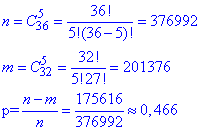
Задача 26. Яка ймовірність роздати 4 тузи з 6 карти, коли в колоді 36?
Розв'язання: Чотири тузи з 4 можна вибрати єдиним способом, залишається вибрати 3 карти з (36-4)=32. Тому кількість сприятливих способів рівна добутку комбінацій
m=C44*C322=1*32*31/2=496.
Всеможлива кількість способів вибрати 6 карт з колоди рівна комбінації з 36 по 6:
n=C366=36!/(6!*30!)=1 947 792.
Вже можна побачити, що ймовірність такої події прямує до нуля
p=m/n=496/1 947 792≈0,00025.
Задача 27. Для того щоб виграти в лотерею потрібно вгадати 4 з 35 цифр. Знайти ймовірність вгадати цифри, якщо вони не повторюються?
Розв'язання:Тут не важливий порядок, а лише правильний набір цифр. Тому нам потрібно знайти кількість способів вибрати 4 різні цифри з 35, а це як Ви здогадались дорівнює С з 35 по 4:
n=C354=35!/(4!*31!)=35*34*33*32/24=52360.
Це і є кількістю різних комбінацій скласти виграшний білет, а він лише один, тому імовірність виграшу:
p=1/52360=0,000019.
Ось чому Вам майже нереально виграти в лотерею, а тим хто організував гральний бізнес завжди залишаються у виграші.
Вчіть ймовірність, щоб знати свої шанси на успіх. Для цього подружіться з факторіалами, адже Вам доведеться їх спрощувати протягом усього курсу теорії ймовірностей.
Наведемо таблицю з правилами, яка вчить коли і яку формулу слід застосовувати.

Приклад 1. Скількома способами можна вишикувати в ряд 7 учнів?
Розв'язування: Першого учня можемо вибрати серед 7, другого серед (7-1)=6, що залишилися, і т.д.
Тому таких способів буде
N=7*6*5*4*3*2*1=5040.
З другої сторони, маємо вибірку всі елементи якої входять в неї, не повторюються, порядок розміщення важливий.
Тому за таблицею вище потрібно застосувати формулу перестановок
N=P7=7!=5040.
Відповідь: 5040.
Приклад 2. Скількома способами можна переставити цифри в числі 978352.
Розв'язування: Всі цифри в шестизначному числі різні, першу цифру можна обрати 6 способами, другу 5 способами(першу вибрано), третю 4 (перші дві вибрано) і т.д.
по правилу множення подій всього способів
6*5*4*3*2*1=720.
або маємо кількість всіх перестановок з 6-х елементів
тому N=Р6=6!=720.
Відповідь: 720.
Приклад 3. Скільки різних чисел можна отримати перестановкою цифр в числі 553334.
Розв'язування: Маємо 6-не число, цифри якого повторюються.
5 - повторюється двічі, 3 - тричі.
Тому тут застосовуємо формулу перестановок з повтореннями
Р6(2,3,1)=6!/(3!*2!*1!)=720/12=60.
Відповідь: 60.
Приклад 4. Скільки різних слів можна скласти перестановкою букв в слові ЗАКАРПАТТЯ.
Розв'язування: Задача, як і попередня на перестановки з повтореннями.
Слово ЗАКАРПАТТЯ має 10 букв,
три букви А та дві Т.
Тому кількість різних "слів" знаходимо з формули
Р10(3,2,1,..)=10!/(3!*2!)=302400.
Відповідь: 302400.
Приклад 5. У мами є 3 яблука і 4 груші. Кожного дня протягом тижня вона видає по одному. Скількома способами це можна зробити?
Розв'язування: Маємо групи {я, г,я, г,я,г,г}. Всього перестановок з 4+3=7 елементів можна зробити 7!, але слід врахувати, що в деяких перестановок одні й ті елементи будуть поміняні тільки місцями, тому їх відкидаємо.
Їх кількість 3!*4!.
В результаті отримаємо:
N=7!/(3!*4!)=35.
Відповідь: 35.
Приклад 6. В поїзді 9 вагонів. Скількома способами можна розсадити 4-х чоловік, щоб вони їхали в різних вагонах.
Розв'язування: Оскільки всі повинні їхати в різних вагонах, то потрібно вибрати 4 вагони з 9 з врахуванням порядку (номера вагонів різні). А це розміщення з 9 по 4, n=9, m=4.
Обчислюємо:
A94 =9!/(9-4)!= 9*8*7*6=3024.
Відповідь: 3024.
Приклад 7. Скількома різними способами можна вибрати 4 книги з 8 книг?
Розв'язування: У вибірку входять не всі елементи, порядок важливий, книги не повторюються.
Тому кількість різних способів обчислюємо за формулою комбінацій з 8 по 4:
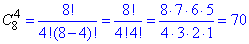
Відповідь: 70.
Приклад 8. В групі 9 чоловіків. Скільки можна утворити різних підгруп при умові, що в підгрупу входить не менше трьох чоловіків?
Розв'язування: Не менше 3-х чоловік, тоді 3+6 або 4+5 чоловік (5+4, 6+3 – ті ж самі комбінації). В кожній вибірці важливий лише склад, оскільки ролі не важливі − тому використовуємо сполучення з n різних елементів по m:
C93=9!/(3!*6!)=84.
Число вибірок з 3-х чоловіків: 84.
С94=9!/(4!*5!)=126.
Число вибірок з 4-х чоловіків: 126.
Сумуємо
N=84+126=210 - підгруп.
Відповідь: 210.
Приклад 9. Яких чисел від 1 до 1 000 000 більше: тих, які містить одиниці в записі, чи тих, в яких одиниця не зустрічається?
Розв'язування: Обчислюємо кількість чисел від 1 до 999999 (число 1 000 000 містить одиницю единицу, тому його відкидаємо), при записі яких не використовуємо одиницю.
Кожну цифру можна вибрати 9 способами (будь-яка цифра окрім 1), тому всі 6 цифр за правилом множення можна вибрати 9^6 способами (якщо в числі до значущих цифр стоять нулі, то ми їх просто відкидаємо). При цьому один варіант (000000) потрібно відкинути, оскільки число 0 не розглядається.
Отримаємо N=96−1=531440 чисел, що не містять одиниці.
Відповідно тих, що містять одиницю буде
1000000-531440= 468560.
Робимо висновок, що чисел без одиниці до мільйона більше, ніж тих що мають одинички.
Приклад 10. Скільки різних дробів можна скласти з чисел 2, 5,7, 11, 13, 17, 21 так, щоб кожний дріб містив два різних числа?
Скільки серед них буде правильних дробів?
Розв'язування: Різних дробів із 7 чисел: 2, 5, 7, 11, 13, 17, 21 можна скласти
C72*2=7!/(2!*6!)*2=42.
(C72 способів вибрати два числа з 7, і двома способами складаємо з них дріб: спершу одне число - чисельник, друге - знаменник, потім навпаки).
Тому серед 42 дробів рівно половина 21 будуть правильними (чисельник менший знаменника):
C72=7!/(2!*5!)=7*6/2=21 спосіб вибрати два числа із 7, і єдиний спосіб скласти дріб, щоб чисельник був менший знаменника.
Відповідь: 30, 15.
Приклад 11. В шахматних змаганнях беруть участь 9 шахістів, причому правила складені так, щоб кожний з них зіграв з іншим одну гру. Скільки всього партій прийшлося організувати на змаганнях?
Розв'язування: Спосіб 1. В одній грі участь беруть 2 гравці, тому потрібно знайти кількість способів вибору 2-х з 9, причому порядок в таких парах не важливий.
Застосовуємо формулу сполучень з 9 по 2
N=С92=9!/(2!*(9-2)!)=9!/(2!*7!)=9*8/2=36.
Спосіб 2. Перший шахіст зіграє 8 партій (з 2-м, 3-м, 4-м, і так до 9-го),
2- ий – 7 партій (з 3-м, 4-м, і т.д. до 9-го, тут враховано, що з першим парія вже була),
3-ій − 16 партійй,
...
8 − 1 партію з 9 гравцем.
Разом:
8+7+..+1=(8+1)/2*8=36.
Відповідь: 36.
Приклад 12. Групу з 20 студентів потрібно розділити на 4 групи, з кількостями в групах рівними 3, 4, 6, 7.
Скількома способами це можна зробити?
Розв'язування: Порядок в групі не важливий, важливо щоб групи мали вказані кількості студентів.
Застосовуємо формулу сполучень.
Першу групу формуємо С з 20 по 3 способами
С203=20!/(3!*17!)=20*19*18/6=1140.
Тоді залишиться вибрати другу групу C з (20-3)=17 по 4 способами,
третю − С з (17-4)=13 по 6 способами,
і четверту С з (13-6)=7 по 7 способами, що рівно 1 способу.
Оскільки одночасно потрібно сформувати 4 групи то за правилом комбінаторного множення отримаємо
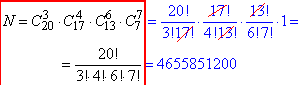
4 групи по 3, 4, 6, 7 студентів можна сформувати 4655851200 способами.
Відповідь:4655851200.
Приклад 13. В одинадцятому класі 35 учнів, серед яких 15 хлопців і 20 дівчат.
Яка ймовірність того, що при виборі 8 чоловік для поїздки на екскурсію будуть вибрані:
1) всі дівчата?
2) шестеро хлопців і дві дівчини?
Розв'язування: Кількість способів вибрати 8 учнів з 35 рівна
n=C(35,8)=35!/(8!*(35-8)!)=23535820.
1) Кількість сприятливих варіантів вибору 8 дівчат серед 20, що можуть їхати, рівна
m=C(20,8)=20!/(8!*12!)=125970.
Ймоврність що поїдуть одні дівчата рівна
p=m/n≈0,0053.
2) Кількість способів вибрати 6 хлопців з 15 і 2 дівчини з 20 рівна
m1=C(15,6)*С(20,2)=15!/(6!*9!)*20!/(2!*18!)=950950.
Тоді ймовірність, що буде вибрано 6 хлопців і 2 дівчини рівна:
p=m1/n≈0,0404.
Відповідь: 0,0053; 0,0404.
Приклад 14. Правління підприємства складається з 9 осіб. Скількома способами можна з цих людей обрати трьох керівників - президента, директора та комерційного директора?
Розв'язування: На роль директора можна обрати 1 з 9 осіб, тоді залишиться 8, тому на роль президента 1 з 8, після чого залишиться 7 кандидатів на роль комерційного директора.
Тому кількість всіх способів обрати трьох керівників рівна:
N=9*8*7=504
Відповідь: 504.
На наступному уроці продовжимо розв'язувати комбінаторні задачі.
Якщо маєте готові розв'язки з комбінаторики, які були б корисними для учнів та студентів, то просимо їх надсилати нам!
чи повторюються елементи у вибірці?
чи важливий порядок розміщення елементів? та
чи всі елементи входять у вибірку?
залежить вибір формули, а отже і правильність обчислень.

Роздрукуйте наведені комбінаторні формули і використовуйте як шпаргалку. Їх завжди можна знайти онлайн, але краще мати під рукою при розв'язуванні наступних завдань. Також вивчайте властивості факторіалів, адже їх постійно доведеться спрощувати.
Задачі з комбінаторики
Приклад 1. Скількома способами можна сформувати потяг з 7 вагонів?
Обчислення: Беремо до уваги, що вагони різні, тому будь-яка перестановка вагонів це інший потяг.
Крім того в формуванні вагонів бере участь вся їх кількість, тому тут використовуємо формулу перестановок P7 :
n=P7=7!=7*6*5*4*3*2*1=5040.
Приклад 2. Скількома способами можна розподілити три різні путівки між 10 працівниками?
Обчислення: Першу путівку можна дати одному з 10 працівників, після чого залишиться 2 путівки і 9 працівників, і останню путівку можна розподілити серед 8 працівників. На мові ймовірностей – це розміщення з 10 по 3:
n=A103=10!/(10-3)!=10*9*8=720.
Приклад 3.В олімпіаді бере участь 7 команд. Скількома способами між ними можна розподілити золоту, срібну та бронзову медалі:
а) якщо одна команда може взяти лише одну медаль?
б) якщо усі команди можуть вибороти кожну з медалей
Обчислення: а) Першу медаль отримає 1 з 7 команд, другу 1 з 6, третю 1 з 5, тому:
m1=A73=7!/(7-3)!=7*6*5=210.
б) За правилом добутку на кожну медаль претендує 7 команд, тому кількість способів рівна 7^3:
m2=7*7*7=343.
Відповідь: 210, 343.
Приклад 4. На столі є 7 ручки та 3 олівці. Скількома способами можна взяти зі столу один предмет?
Обчислення: Взяти один предмет означає або олівець, або ручку. На мові ймовірності всюди "або" замінюємо додаванням.
1 ручку з 4 можна вибрати 4 способами,
1з 3 олівців вибирають 3 способами.
Сумарно
n=7+3=10.
Відповідь: 10.
Приклад 5. Скільки різних п'ятицифрових чисел можна скласти з цифр 2, 3, 4, 5, 6, 7, 8?
Обчислення: Не всі цифри з вибірки (7 цифр) входять у п'ятицифрове число + цифри не повторюються і порядок має значення, тому використовуємо формулу розміщень без повторень
n=A75=7!\2!=2520.
Відповідь: 2520.
Приклад 6. Скільки різних тризначних чисел можна скласти з цифр 0, 1, 2, 3, 4, 5?
Обчислення: Подібні приклади є винятком з правил, тому що "0" на перше місце поставити не можемо. Залишається 5 цифр з 6, тоді за першою не рівною нулю йдуть розміщення з 5 інших цифр по 2:
n=5*A52=5*5!/3!=100.
Відповідь: 100.
Приклад 7. У кошику 6 мандаринів та 8 апельсинів. Остап вибирає або мандарин, або апельсин. Після цього Софія вибирає з фруктів, що залишилися, мандарин й апельсин одночасно. Скільки можливостей такого вибору?
Обчислення: Від вибору Остапа залежить з якого набору буде вибирати Софія. Якщо Остап вибере мандаринку 1 з 6 способами, то Софії буде мати вибір з 6-1=5 мандарин і 8 апельсин (5*8), в іншому разі вона зможе обрати з 6 мандарин і 7 апельсин (6*7). Або такий або такий набір означає, що потрібно застосувати правило суми ймовірностей.
n=6*5*8+8*6*7=240+336=576.
Відповідь: 576.
Приклад 8. У маленької Юлі є багато синіх, червоних, жовтих та зелених кубиків.
(а) Скільки різних веж висотою в 6 кубиків може побудувати Юля?
(б) Скільки серед цих веж містять хоча б один синій кубик?
(в) Скільки серед цих веж містять хоча б один синій або зелений кубик?
Обчислення: Тут потрібно буде використати протилежну подію до двох останніх пунктів задачі.
а) Кожен ряд вежі можна викласти з синього, червоного, жовтого та зеленого кубика. Тобто одного з чотирьох кольорів, тому різних веж може бути
n=4^6=4096.
б) Хоча б один синій кубик означає, або один або два ... або 6. Це передбачає багато обчислень, простіше від всеможливої кількості веж відняти протилежну подію - не містить жодного синього кубика. А це означає, що вежі формуються з 3 кольорів - зелений,жовтий, червоний.
Тому їх кількість рівна
m=n-3^6=4096-729=3367.
в) Логічно, що веж, що містять хоча б один синій або зелений кубик має бути більше ніж тих, що містять хоча б один синій. Але як це врахувати?
І знову приходить на допомогу теорема про протилежну подію, від всіх знайдених віднімемо ті, що не містять ні синього ні зеленого кубика.
Думаю, що тепер Ви здогадалися подальші обчислення. Від n=4096 віднімемо всі, що складаються лише з червоного та жовтого кубика, а їх буде 2^6:
m2=n-2^6=4096-64=4032.
Відповідь: 4096, 3367, 4032.
Приклад 9. Скількома способами можна вибрати 2 білі і 1 рожеву троянду з 10 білих і 5 рожевих троянд?
Обчислення: Завдання на множення ймовірностей. Оскільки порядок входження троянд в букет не важливий, то потрібно застосувати формулу комбінацій, а не розміщень, тому кількість способів вибрати 2 білі з 10 рівна C102:
m1=C102=10!/(8!*2!)=45.
Тоді одну рожеву з 5 можна вибрати 5 способами m2=5.
Загальна кількість вибрати 1 рожеву та 2 білі троянду за формулою множення ймовірностей рівна
n=m1*m2=45*5=225.
Відповідь: 225.
Приклад 10. Скількома способами можна вибрати чотирьох чергових із класу, у якому 15 учнів?
Обчислення: Тут нам неважливий порядок входження, а лише потрібно знайти кількість різних груп по 4 чергових з 15. Тому кількість способів рівна комбінації з 15 по 4:
n=C154=15!/(11!*4!)=15*14*13*12/(4*3*2*1)=1365.
Приклад 11. Скількома способами можна розділити 6 різних цукерок між трьома дітьми, якщо кожна дитина отримує по дві цукерки?
Обчислення: Перше, що ви маєте зауважити це те, що цукерки різні, тому вже слід застосовувати комбінації (сполучення).
Другий момент – це як розподілити, якщо порівно, то всі матимуть по 6:3=2 цукерки, якщо ні – то кількість способів росте.
Підемо простим шляхом, поділимо порівну, тоді перша дитина отримає 2 з 6 цукерок, друга – 2 з 4, третя 2 з 2.
За теоремою множення
n=C62*C42*C22=6!/(4!*2!)*(4!/(2!*2!))*1=15*6*1=90.
Відповідь: 90.
Приклад 12.Скільки різних "слів" можна отримати, переставляючи букви в слові "Математика"?
Обчислення: Оскільки слово "Математика" має букви, що повторяються, то використовуємо перестановки з повтореннями.
Всього "Математика" має 10 букв, дві букви "м" і три "а".
Тому кількість перестановок рівна
n=P10(2,3)=10!/(2!*3!)=302400.
Відповідь: 302400.
Приклад 13.Скільки різних "слів", у яких комбінація букв "бук" йде разом можна отримати, переставляючи букви в слові "букварик"?
Обчислення: Нові "слова" повинні містити "бук" як одну букву, тому переміщати будемо
"бук" "в" "а" "р" "и" "к", тобто 6 "букв".
Для знаходження кількості слів використовуємо формулу перестановок
n=P6=6!=720.
Відповідь: 720.
Приклад 14. В колоді 36 карт, з них 4 тузи. Скількома способами можна вибрати 5 карт так, щоб серед них було 3 тузи?
Обчислення: Порядок входження нас не цікавить, головне набір в якому 3 тузи і 2 інші карти.
3 тузи з 4 можна вибрати C43 способами, лишається 36-4=32 карти, з яких 2 вибираємо C322 способами.
За правилом множення ймовірностей дістанемо:
n=C43*C322=4*(32*31/2)=1984.
Приклад 15. З колоди з 52 карти навмання взяли 4 карт. В скількох випадках буде хоча б одна шістка?
Обчислення:Обчислимо виходячи з протилежної події.
Кількість різних наборів з 52 карт по 4 рівна C524, але серед них є ті, що не містять шістки. Тому від знайденої кількості віднімемо випадки коли серед 4 карт немає 6. Це можливо, коли вибираємо 4 з 52-4=48 (віднімаємо чотири 6 з колоди).
Таких наборів буде C484.
Остаточно отримаємо:
n=C524-C484=52*53*51*50/(4*3*2)-48*47*46*45/(4*3*2)=292825-194580=98245.
Ось така непроста комбінаторика!
Тут головне знати комбінації чи перестановки використовувати, та чи важливі повторення, все решта зводиться до вибору формули та вміння спрощувати факторіали.
Уважно перегляньте алгоритми обчислень, оскільки на їх основі побудовані складніші задачі з ймовірності, які чекають Вас на практичних, розрахункових, тестах. Цікаві комбінаторні завдання поступово будуть оформлені в нові уроки, оскільки в 15 прикладах всіх нюансів важко пояснити.
Означення: події А і B називаються незалежноими, якщо ймовірність кожної з них не залежить чи відбулась інша подія.
P(A/B)=P(A), P(B/A)=P(B).
Незалежність подій має взаємну властивість: якщо подія A не залежить від події B, то і подія B не змінює A. Те саме стосується незалежності спряжених, тобто протилежних подій.
Теорема множення ймовірностей:
Ймовірність добутку двох незалежних подій А,В дорівнює добутку ймовірностей цих подій
Р(А*В) = Р(А)•Р(В).
Формула поширюється на будь-яку кількість незалежних між собою подій
Р(А1..An) = Р(А)•...•Р(An).
І для себе щоб знали, що добуток двох чи більше незалежних подій, це також подія, тому можна записати
С=А•В, Р(С) = Р(А)•Р(В).
Приклад 1. Гральний кубик кидають двічі. Знайти ймовірність того, що:
1) обидва рази випаде непарна кількість очок?
2) перший раз випаде парна кількість очок, а другий кратна трьом?
Яка з подій ймовірніша?
Обчислення: Випишемо, які значення можуть випасти при однократному підкиданні кубика
{1, 2, 3, 4, 5, 6}.
Їх кількість рівна 6.
1) Подія A - випала непарна кількість очок, тобто одне з чисел
{1, 3, 5}.
Ймовірність такої події рівна
P(A)=3/6=1/2.
так як кількість сприятливих випадків події size(A)=3.
Подія B -підкидання двічі кубика є добутком незалежних подій, тому ймовірність рівна
P(B)=P(A)•P(A)=1/2•1/2=1/4.
2) Множина сприятливих подій - парна кількість очок
{2,4,6}. p1=3/6=1/2.
Кратних трьом є тільки дві грані грального кубика
{3,6}. p2=2/6=1/3.
Тому ймовірність події С, що перший раз випаде парна кількість, а другий кратна трьом рівна
P(С)=p1•p2=1/2•1/3=1/6.
Порівнянням ймовірностей 1/4>1/6 переконуємося, що перша подія має більші шанси відбутися.
Відповідь: 1/4, 1/6, перша.
Приклад 2.У двох бочках плавають карасі і коропи в перемішку. В першій бочці 60% карасів, в другій 70%. Навмання з першого і другого контейнеру виловлюють по рибі. Яка ймовірність, що:
1) виловлять тільки карасів;
2) виловлять риб одного сорту;
3) виловлять різні риби.
Вважати, що кількість риб в бочках однакова.
Обчислення: Нехай подія А- виловили карася з першої бочки, B-з другої бочки. Тоді ймовірності подій А та B
p(A)=60%/100%=0,6.
p(B)=70%/100%=0,7.
Ймовірності протилежних подій - виловили коропа відповідно рівні
p(-A)=1-0,6=0,4;
p(-B)=1-0,7=0,3.
1) Подія С - виловить тільки карасів. За теоремою множення ймовірностей обчислюємо p(C):
P(C)=p(AB)=p(A)•p(B)=0,6•0,7=0,42.
2) Подія D - виловлять риб одного сорту означає, що або карасів або коропів виловлять з двох бочок.
"Або" в ймовірності відповідає за додавання ймовірностей
P(D)=p(A)•p(B)+p(-A)•p(-B)=p(C)+0,4•0,3=0,54.
3) Виловлять різні риби (E), означає, що або з першої бочки карася і з другої коропа, або з першої коропа і з другої карася. Інших варіантів немає, проте слід про обидва варіанти не забувати на практиці.
Тому через добуток ймовірностей обчислюємо
P(E)= p(A)•p(-B)+p(-A)•p(B)=0,6•0,3+0,4•0,7=0,46.
Відповідь: 0,42; 0,54; 0,46.
Приклад 3. У трьох партіях 90%, 80% і 70% доброякісних виробів відповідно. Навмання вибирають по одному виробу із кожної партї. Яка ймовірність виявити серед них: а) хоча б один недоброякісний виріб; б) лише один недоброякісний виріб в) три недоброякісні вироби?
Обчислення: Подія C - хоча б один недоброякісний є протилежною до всі якісні. Тому щоб не виконувати громіздких обчислень від повної ймовірності віднімемо ймовірність протилежної події
P(С)=1-p1•p2•p3=1-0,9•0,8•0,7=0,504.
Подія D -лише один недоброякісний, означає, що один недоброякісний, а решта добрі, і так для кожної можливої партії, тому ймовірність рівна P(D)=q1•p2•p3+p1•q2•p3+p1•p2•q3=0,1•0,8•0,7+0,9•0,2•0,7+0,9•0,8•0,3=0,2481.
Ймовірність вибрати три неякісних вироби (F) рівна добутку трьох ймовірностей q:
P(F)=q1•q2•q3=0,1•0,2•0,3=0,006.
Відповідь:0,504; 0,2481; 0,006.
Приклад 4. Три стрільці незалежно один від одного стріляють по мішені. Ймовірність влучення в мішень для першого дорівнює 0,7, для другого - 0,8, для третього – 0,9.
1) Яка ймовірність, що всі влучать?
2) Знайти ймовірність, що ніхто не влучить
3) Яка ймовірність, що хоча б двоє з них влучить?
4) Яка ймовірність, що влучить лише один стрілець?
5) Знайти ймовірність, що не більше одного стрільця влучиь по мішені.
Обчислення: Уважно проаналізуйте готові відповіді до завдання. Це дасть Вам ширше уявлення, як такі задачі розв'язувати.
Багато онлайн ресурсів пропонують розв'язки прикладів не загострюючи Вашої уваги на деталях обчислень.
Випишемо з умови ймовірності влучань стрільців та обчислимо ймовірності протилежної події – "не влучили"
p1=0,7; q1=1-0,7=0,3;
p2=0,8; q2=1-0,8=0,2;
p3=0,9; q3=1-0,9=0,1.
Постріли по мішені є незалежними подіями, стрільці один на одного не впливають.
1) За теоремою множення подій імовірність, що всі влучать рівна
P1=p1•p2•p3=0,7•0,8•0,9=0,504.
2) Умова, що ніхто не влучив, означає, що ні перший, ні другий, ні третій стрілець не влучив у ціль.
Цьому відповідає добуток ймовірностей протилежних подій
P2=q1•q2•q3=0,3•0,2•0,1=0,006.
3) Подія хоча б двоє влучать рівносильна тому, що або двоє з трьох або всі троє влучать (вже знаємо з (1)).
"Або" на мові ймовірностей означає додавання ймовірностей.
Оскільки події між собою незалежні то застосовуємо теорему про добуток ймовірностей
P(A)=p1•p2•q3+q1•p2•p3+p1•q2•p3+p1•p2•p3=
=0,7•0,8•0,1+0,3•0,8•0,9+0,7•0,2•0,9+0,504=0,628.
4) Ймовірність, що влучить один стрілець означає, що один з трьох. Або перший, або другий, або третій.
Тому в формулі ймовірностей дістанемо суму добутків вигляду
P4=p1•q2•q3+q1•p2•q3+q1•q2•p3=
=0,7•0,2•0,1+0,3•0,8•0,1+0,3•0,2•0,9=0,092.
5) Ймовірність, що не більше одного стрільця влучить по мішені означає, що або один з трьох влучить або ніхто з них не влучить. Такі ймовірності вже знайдені в пункті 2) і 4), тому залишилося їх просумувати:
P5=P2+P4=0,006+0,0092=0,0152.
Відповідь: 0,504; 0,006; 0,628; 0,092.
Приклад 5. Робітник обслуговує три верстати. Ймовірність того, що протягом години його уваги не буде потребувати перший верстат, дорівнює 0,8, другий – 0,6, третій – 0,5. Визначити ймовірність того, що протягом години уваги робітника
а) не будуть вимагати рівно два верстати;
b) вимагатимуть усі верстати.
с) вимагає не більше одного верстату.
d) яка з попередніх подій найвірогідніша?
Обчислення: а) Подія А полягає в тому, що увагу не вимагають 2 з 3 верстатів, тобто потрібна увага до одного з 3 верстатів.
Позначимо
p1=0,8, p2=0,6, p3=0,5 – ймовірності, що відповідні верстати не вимагають уваги.
Тоді
q1=1-0,8=0,2
q2=1-0,6=0,4
q3=1-0,5=0,5 – ймовірності, що 1, 2, 3 –й верстати вимагають уваги.
Уваги потребує один з тьох означає або перший, або другий, або третій.
На мові ймовірності "або" означає додавання "+", тому ймовірність події рівна:
P(A)=q1*p2*p3+p1*q2*p3+p1*p2*q3=
= 0,2*0,6*0,5+0,8*0,4*0,5+0,8*0,6*0,5=0,46
b) Подія В – уваги вимагають усі три верстати.
Ймовірність такої події рівна
p(B)=q1*q2*q3=0,2*0,4*0,5=0,04
c) Подія C – уваги вимагагає не більше одного верстата означає, що або 1 з 3 вимагає уваги або жодного.
Один з трьох вимагає уваги це те ж саме, що 2 з 3 не вимагають, тому ймовірність такої події згідно пункту а) рівна 0,46.
Ймовірність, що жоден не вимагає рівна
p(0)=p1*p2*p3=0,8*0,6*0,5=0,24
За правилом сумування ймовірностей знаходимо p(C):
p(C)=0,46+0,24=0,7
d) Найвірогідніша та з подій A, B, C, у якої ймовірність вища. Порівнюючи значення приходимо до висновку, що найвірогідніше уваги вимагає не більше одного верстату.
Приклад 6. В квадрат зі стороною 4 см вписано круг, що дотикається до сторін квадрата. Знайти ймовірність, що серед двох точок кинутих в квадрат:
1) обидві попадуть в круг;
2) жодна не попаде в круг.
Відповідь округлити до тисячних.
Обчислення:Задача на геометричну ймовірність. Побудуємо допоміжний рисунок до задачі

Ймовірності потрапити точці в одну з фігур будуть пропорційні їх площам, це Ви маєте усвідомити і використовувати при обчисленні подібних задач.
Площа круга зі стороною a=4 см рівна S1=4•4=16 см2, площа круга радіусом r=2 см рівна S2=π•r^2=4π≈12,56 см2.
Ймовірність, що точка кинута в квадрат попаде в круг рівна
p(A)=S2/S1=12,56/16≈0,785.
1) Оскільки кидання точок є незалежними подіями, то ймовірність, що обидві попадуть в круг (B) рівна
p(B)=p(A)•p(A)=0,785•0,785≈0,616.
2) Подія C, що точка не попаде в круг є протилежною до події А, тому її ймовірність визначимо віднявши від повної ймовірності P(А):
P(C)=1-p(A)=1-0,785=0,215.
Такий результат можна отримати, якщо площу за межами круга (зафарбовано жовтим) розділити на площу круга
P(C)=(S1-S2)/S1=(16-12,56)/16=0,215.
За теоремою множення ймовірностей обчислимо імовірність, що обидві точки не попадуть в круг
P=P(C)•P(C)=0,215•0,215≈0,046.
Відповідь: 0,785; 0,046.
Задачі на самопідготовку з теми "Теорема множення ймовірностей незалежних подій"
Задача 1. Екзаменаційний білет містить три питання. Ймовірність того, що студент знає відповідь на перше питання-0,7, друге -0,8, третє - 0,9.
Знайти ймовірність, що студент відповів правильно на:
1) всі питання;
2) 2 з 3 питань.
3) Яка ймовірність, що студент відповів правильно тільки на одне питання?
Задача 2. Конвеєр випускає деталі, 90% яких стандартні. Для контролю якості робітник відбирає три деталі.
Яка ймовірність, що:
1) всі деталі стандартні?
2) лише перша нестандартна з 3?
3) хоча б дві деталі стандартні?
Задача 3. Підкидають гральний кубик тричі. Яка ймоврність, що випаде три шістки?
Яка ймовірність, що першим випаде просте число, а наступними кратні 2?
Знайти ймовірність, що на крайніх кубиках випадуть одинички, а всередині парне число?
На сайті Вас чекають нові готові відповіді до завдань з ймовірності, диф. рівнянь, геометрії, переходіть і вивчайте всеможливі алгоритми розв'язання прикладів.
]]>Елементи комбінаторики
Вибір формули для обчислення сполук
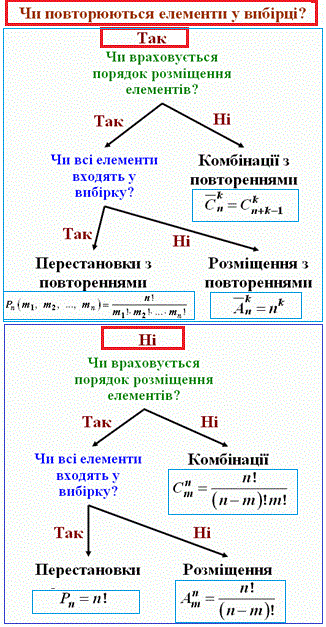
Відомі два базові правила, за якими приймають рішення:
якою формулою комбінаторики слід користуватися?
Чи це будуть комбінації, перестановки чи розміщення залежить від відповіді на два питання.
1) Чи враховується порядок розміщення елементів?
Якщо відповідь «ні» то застосовуємо формулу комбінацій.
Якщо «так», то маємо два варіанти, які залежать від відповіді на наступне питання:
2) Чи всі елементи входять у вибірку (сполуку)?
Якщо «так» то обчислюємо через перестановки, якщо «ні» застосовуємо формулу розміщень.
Щоб легше запам'ятались ці правила наведемо наступний рисунок, вивчивши який у Вас не виникатиме труднощів з основними комбінаторними задачами.
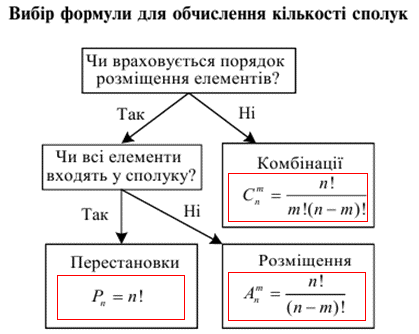
Правила комбінаторного додавання та комбінаторного множення
Правило комбінаторного множення є частковим випадком основного правила комбінаторики: Нехай необхідно виконати послідовно n дій. При цьому першу дію можна виконати k1 способами, другу — k2 способами і так далі до m-ї дії, яку можна виконати km способами.
Тоді всі m дій можна виконати
k1 • k2 • ... • km1 • km2 • ... • km способами.

Скількома способами?
Почнемо з простих прикладів, які Вам допоможуть у вивченні формул.
Приклад 1. Скількома способами можна розставити на полиці 5 різних книжок?
Розв’язання: Спершу обчислимо за допомогою логічних висновків. На перше місце можемо поставити одну з 5 книг, на друге – одну з 4 (оскільки одна вже вибрана на перше місце), на 3 – одну з 3, 4 – одну з 2, і на останнє місце можна поставити ту книгу що залишилася.
Кількість способів розставити книгу рівна добутку кількості варіантів вибрати книгу на кожне місце, тобто
5!=5•4•3•2•1=120 способів.
Тепер розв’яжемо через формули комбінаторики.
Для цього дамо відповідь на 2 запитання описані на початку:
1) Чи враховується порядок розміщення елементів? Так.
2) Чи всі елементи входять до сполуки? Так.
В такому разі обчислюємо перестановки 5 книг
P5=5!= 5•4•3•2•1=120
Відповідь: 120 способів.
Приклад 2. Телефонні номера на початку містять номер операторів 068, 067, 097, 098, а далі йдуть 7 номерів телефону абонента.
Скільки телефонних семизначних номерів можна скласти з цифр від 1 до 9 при умові, що цифри у номері не повторюються?
Розв’язання: Дану задачу можна обчислювати як логічно так і через формули, при великих значеннях цифр або складніших початкових умовах задач логіка вас може підвести, а от формули – ні.
1) Чи враховується порядок розміщення елементів? Так.
2) Чи всі елементи входять до сполуки? Ні, оскільки маємо 9 цифр, а потрібно вибрати 7 із них.
Тоді за наведеною схемою застосовуємо формулу розміщень
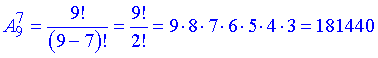
Отримали 181 тисячу 440 різних номерів, в яких цифри від 1 до 9 не повторюються.
Приклад 3. Скількома способами можна вибрати 3 різні фарби із 5 різних фарб?
Розв’язання: Маємо задачу на розміщення (подусайте чому) і алгоритм розрахунків ідентичний до попередньго завдання.
Першою можемо вибрати одну з 5 фарб, другою одну з 4 і третьою одну з 3.
Кількість способів рівна добутку 5•4•3=60 способів.
ІІ спосіб
Перевіряємо умову
1) Чи враховується порядок розміщення елементів? Так.
2) Чи всі елементи входять до сполуки? Ні, тому що маємо 5 різних фарб і всього 3 місця на які їх можна вибрати.
Застосовуємо формулу розміщень з 5 по 3
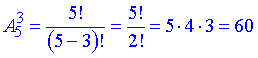
Відповідь: 60.
Приклад 4. Скількома способами можна з 20 чоловік призначити двох чергових з однаковими обов’язками?
Розв’язання: Всі хто хотів робити по аналогії з попередніми завданнями отримають у відповідь 20•19=380, що є неправильним.
А все тому, що маємо підказку «чергові з однаковими обов’язками», тобто Андрій, Василь чи Василь, Андрій є одним і тим самим, однією комбінацією.
А на перше питання «Чи враховується порядок розміщення елементів?» маємо відповідь «Ні».
Тому тут слід використовувати формулу комбінацій з 20 чоловік по 2
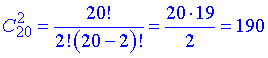
Уважно перегляньте як спрощують факторіали, без розуміння цього Вам доведеться малювати дроби на ширину листка.
Відповідь: є 190 способів вибрати 2 чергових з 20 з однаковими обов’язками.
Приклад 5. Скільки прямих можна побудувати через 10 різних точок?
Розв’язання: З курсу геометрії відомо, що пряму можна побудувати через 2 точки.
Припустимо, що задані точки не лежать на одній прямій, оскільки в протилежному випадку задача буде невизначеною.
Далі нам неважливий порядок розміщення точок на прямій, що веде до застосування формули комбінацій з 10 по 2
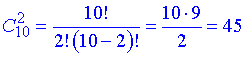
Відповідь: через 10 точок можна побудувати 45 прямих.
Поєднання елементів комбінаторики та комбінаторного множення з додаванням
Далі наведені складніші комбінаторні задачі, які вимагають при обчисленнях застосування однієї з формул комбінаторики + правило додавання або множення, тому уважно перегляньте, як обчислювати коли маємо в умові «І» та «АБО».
Приклад 6. У підрозділі 3 офіцерів та 49 солдат.
Скількома способами можна виділити наряд, який складається із 2 солдат і двох офіцерів?
Розв’язання: Нам неважливо порядок входження офіцерів та солдат в наряд, тому тут застосовуємо комбінації.
Вибрати 2 солдат із 49 можна через комбінації з 49 по 2, офіцерів – з 3 по 2.
Нам потрібно вибрати і солдат і офіцерів, тому застосовуємо формулу комбінаторного множення
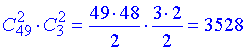
Відповідь: 3528 способами.
Приклад 7. Із 10 троянд і 5 жоржин та 7 ромашок треба скласти букет так, щоб в ньому були по 3 квітки з кожного сорту.
Скількома способами можна скласти букет?
Розв’язання: Порядок входження квітів неважливий, тому через комбінації знаходимо кількість способів вибрати 3 троянди з 10, 3 жоржини з 5 та 3 ромашки з 7.
Далі оскільки маємо букет, то потрібно і ті, і інші квіти. А це правило множення, тому відповіддю буде добуток натупних комбінацій
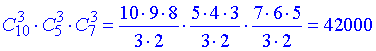
Відповідь: 42000 способів.
Приклад 8. Із шести бігунів і трьох стрибунів треба скласти команду із 4 чоловік, в яку б входив хоча би один стрибун.
Скількома способами це можна зробити?
Розв’язання: Умова хоча б один стрибун при виборі з 3 означає, що або 1 або 2 або 3 стрибуни можна вибирати.
При цьому залишається вибрати ще 3 з шести бігунів для 1 стрибуна,
або 2 з 6 бігунів для 2 стрибунів і
1 з 6 для 3 стрибунів.
Умова «або» означає, що потрібно застосувати комбінаторну формулу додавання.
В підсумку отримаємо суму добутків комбінацій
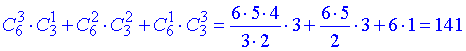
Відповідь: 141 способом.
Складні комбінаторні задачі
Задача 1.26 Скількома способами можна з колоди 36 карт взяти 10 карт так, щоб серед них було точно 8 карт однієї масті?
Розв'язання: В колоді з 36 карт є 4 масті по 9 карт, тому спочатку вибираємо 1 масть з 4 (без повторень, порядок неважливий) через комбінацію з 4 по 1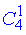 ;
;
з тих 9 карт вибираємо 8 за умовою задачі (без повторень, порядок неважливий) також через комбінацію з 9 по 8 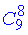 ;
;
а потім вибираємо інші 2 карти вже з 36-9=27 карт, що залишились (без повторень, порядок неважливий) за аналогічними до попередніх формулами 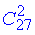
Досі тричі застосували формулу комбінацій, але це ще не є кінцевою відповіддю.
Далі використовуємо комбінаторне множення, оскільки маємо три «і»
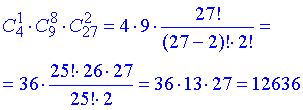
Отже є 12636 способів виконати умови завдання.
Задача 1.27 Скількома способами можна вибрати 6 карт з 52, щоб серед них були карти всіх 4 мастей?
Розв'язання: В колоді з 52 карт є 4 масті по 13 карт, тому:
І) спочатку вибираємо 1 масть з 4 (без повторень, порядок неважливий) 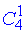 ;
;
з тих 13 карт вибираємо 3 (без повторень, порядок неважливий) 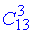 ;
;
з інших 3-х мастей вибираємо по 1 карті (без повторень, порядок неважливий)
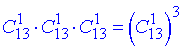 , або
, або
ІІ) спочатку вибираємо 2 масті з 4 (без повторень, порядок неважливий) 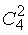 ;
;
з тих 13 карт однієї масті і 13 карт іншої масті вибираємо 2 карти (без повторень, порядок неважливий)
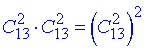
з інших 2-х мастей вибираємо по 1 карті (без повторень, порядок неважливий)
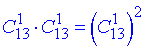
а далі застосовуємо комбінаторне додавання
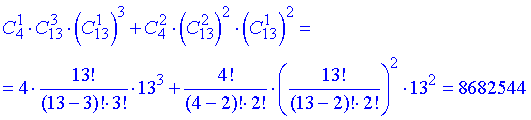
Задача 1.35 Скільки різних «слів» можна утворити перестановкою літер у слові «паралелепіпед»?
Розв'язання: В слові «паралелепіпед» є 13 літер, серед яких 3 – «п», 2 – «а», 1 – «р», 2 – «л», 3 – «е», 1 – «і», 1 – «д».
Маємо перестановку, в якій важливий порядок і елементи повторюються певну кількість разів, тому така кількість рівна перестановкам
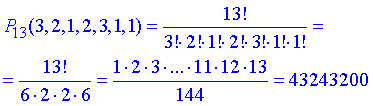
Отримали 43 мільйони 243 тисячі 200 різних наборів перестановок букв.
Задача 1.40 Протягом сесії студенти складають 4 іспити, з яких 2 – з математики.
Скількома способами можна скласти розклад так, щоб іспити з математики не стояли поруч?
Розв'язання: Дана задача дещо двозначна: предмети математики є різні (наприклад алгебра і геометрія), тому їх порядок потрібно враховувати. І тут є два варіанти:
іспити з математики мають йти за порядком або їх можна переставляти.
Якщо можна переставляти, тоді справедливі наступні міркування: з 4-х іспитів предмет з математики може стояти або першим, або останнім.
Якщо іспит з математики стоїть першим, то наступний не буде з математики, далі залишається вибрати ще 2 предмета з 3-х (без повторень, порядок важливий):  , результат будемо множити на 2, оскільки врахуємо і зворотній порядок (від 4-го до 1-го іспиту), тому отримаємо 12 способів.
, результат будемо множити на 2, оскільки врахуємо і зворотній порядок (від 4-го до 1-го іспиту), тому отримаємо 12 способів.
 способів.
способів.
Якщо іспити з математики не можна міняти порядком то різних способів вдвоє менше – 6.
Їх не багато, тому можемо всіх виписати, позначивши цифрами номера екзаменів з математики, а латинськими буквами два інші екзамени.
1а3b
1b3a
a2b4
b2a4
1ab4
1ba4
Це і є шукані 6 способів, якщо якщо екзамени з математики не можна переставляти місцями.
Завдання (номера) в попередніх задачах взяті з навчального посібника:
Бордуляк М. Т. Теореми і задачі теорії ймовірності: навч. посібн. / М. Т. Бордуляк, О. Б. Скасків, О. М. Сумик, І. Е. Чижиков – Львів: Видавець І. Е. Чижиков, 2013. – 175 с. – (Серія «Математичний практикум»).
Нехай для кожного досліду імовірність появи події A постійна P(A)=p, ймовірність протилежної події визначається залежністю
 Потрібно знайти ймовірність появи події A рівно m раз в серії із n випробувань. При цьому варто зазначити, що подія A в серії дослідів може чергуватися любим способом, головне щоб виконалася рівно m раз.
Потрібно знайти ймовірність появи події A рівно m раз в серії із n випробувань. При цьому варто зазначити, що подія A в серії дослідів може чергуватися любим способом, головне щоб виконалася рівно m раз.
Результати випробувань для зручності позначаємо літерою A у випадку появи події і "А спряжене" для протилежної.
для протилежної.
Випробування в яких A відбувається m раз, і не відбувається (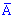 ) n-m за означенням будуть сприятливими. Їх кількість N рівна кількості способів вибору m елементів із n і визначається за формулою сполучень
) n-m за означенням будуть сприятливими. Їх кількість N рівна кількості способів вибору m елементів із n і визначається за формулою сполучень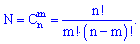 Визначимо імовірність сприятливої комбінації (в серії з n випробувань появи події A рівно m раз). Для простоти запису розглянемо випадок коли подія A відбулася в перших дослідах і не відбулася в решта n-m. Схематично її можна позначити наступним чином, при цьому ймовірність визначити за теоремою множення ймовірностей
Визначимо імовірність сприятливої комбінації (в серії з n випробувань появи події A рівно m раз). Для простоти запису розглянемо випадок коли подія A відбулася в перших дослідах і не відбулася в решта n-m. Схематично її можна позначити наступним чином, при цьому ймовірність визначити за теоремою множення ймовірностей Для інших сприятливих випробувань Pi ймовірність буде така ж, тільки порядок їх в серії з експериментів буде змінюватися
Для інших сприятливих випробувань Pi ймовірність буде така ж, тільки порядок їх в серії з експериментів буде змінюватися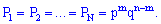 Всі сприятливі випробування є попарно несумісними, тому для знаходження шуканої ймовірності їх потрібно просумувати
Всі сприятливі випробування є попарно несумісними, тому для знаходження шуканої ймовірності їх потрібно просумувати або
або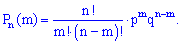
Вивів її вперше швейцарський математик Якоб Бернуллі (1654 р.–1705 р.), за ним і збереглася назва формули.
Якщо просумувати ймовірність всіх випробувань в яких подія A може відбутися від нуля до 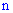 разів в серії із n випробувань то отримаємо повну ймовірність
разів в серії із n випробувань то отримаємо повну ймовірність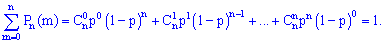 Доданки цієї суми співпадають по вигляду з розкладом бінома Ньютона
Доданки цієї суми співпадають по вигляду з розкладом бінома Ньютона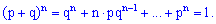 Легко переконатися, що сума рівна одиниці
Легко переконатися, що сума рівна одиниці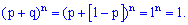 В літературі можна зустріти термін "біноміальний розклад ймовірностей", це якраз множина всіх ймовірностей, яка просумована вище.
В літературі можна зустріти термін "біноміальний розклад ймовірностей", це якраз множина всіх ймовірностей, яка просумована вище.
Як наслідки, з формули Бернуллі виводяться наступні формули для популярних для практики задач:
1) ймовірність появи події A "хоча б один раз" в серії з n випробувань
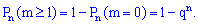
2) ймовірність появи події A "хоча б певну кількість k раз" в серії з n випробувань обчислюють за формулою
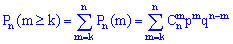
або за властивістю біноміального розкладу ймовірностей
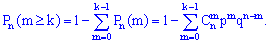
На основі даної залежності вводять в розгляд твірну функцію, яка дає змогу визначити можливу кількість появи події A в серії з n випробувань
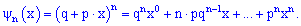
За властивістю твірної функції множники при певному m степені змінної (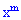 ) дорівнюють імовірності появи події A в серії з n дослідів рівно m раз. Це легко прослідкувати з формули сумування імовірностей всіх можливих випробувань за схемою Бернуллі.
) дорівнюють імовірності появи події A в серії з n дослідів рівно m раз. Це легко прослідкувати з формули сумування імовірностей всіх можливих випробувань за схемою Бернуллі.
Якщо ймовірності появи події в кожному досліді різні P(Ai)=pi, а протилежної 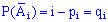 , то за властивостю твірної функції ймовірність події A відбутися m раз в серії n дослідів рівна множнику при xm в розкладі функції за степенями x
, то за властивостю твірної функції ймовірність події A відбутися m раз в серії n дослідів рівна множнику при xm в розкладі функції за степенями x
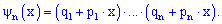
Вона достатньо часто зустрічається при розв'язуванні задач, в яких ймовірності появи події A в кожному наступному досліді змінюються та дозволяє при невеликій кількості m появи події A швидко знайти імовірність (розв'язок задачі).
Найімовірніша число k0 появи події A в схемі Бернуллі лежить в інтервалі
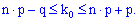
Для застосування схеми Бернуллі потрібно щоб виконувалися три умови:
1) досліди повинні бути незалежні між собою;
2) кожен дослід повинен мати два результати A , протилежна до неї 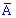 і ніяких інших варіантів;
і ніяких інших варіантів;
3) ймовірність появи події A повинна бути однаковою для кожного наступного досліду.
Розглянемо схему розв'язування типових задач.
Приклад 1. В тирі стрілець проводить 7 пострілів по мішені з ймовірністю улучення кожного 0,8.
Яка ймовірність того, що буде:
а) рівно 4 влучення;
б) не менше за 5 влучень;
в) не більше двох влучань.
Розв'язок. а) проводиться т=7 незалежних одне від одного дослідів з ймовірністю влучення в мішень в кожному з них рівною p=0,8. Ймовірність того, що буде рівно m=4 влучань обчислюємо за формулою Бернуллі:
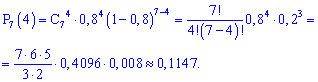
Вона становить p=0,1147.
б) подію A, яка полягає в тому, що при n=7 пострілах буде не менше за 5 влучань можна розглядати як суму трьох несумісних подій: B – 5 влучань з 7, подія C – 6 влучань з 7 і D – всі 7 пострілів влучні.
За формулою Бернуллі знаходимо імовірності подій
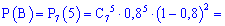
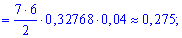
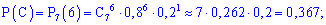
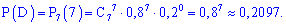
Тоді ймовірність шуканої події A рівна сумі знайдених імовірностей
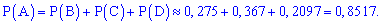
в) Подібним чином ймовірність події A – не більше двох влучань при семи пострілах можна обчислити, як суму ймовірностей трьох подій:
B – 2 влучення з 7,
C – 1 з 7,
D – жодного влучання із 7 пострілів (7 промахів).
На практиці студенти часто забувають розглядати події подібні до жодного влучання D , тож не робіть подібних помилок і Ви, та добре запам'ятайте можливість виникнення такого варіанту. Імовірності знаходимо за знайомою вже формулою
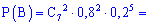
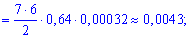
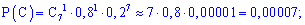
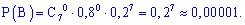
Сумуючи ймовірності одержимо

Однак події A (не більше трьох влучень при п'яти пострілах) і (не менше чотирьох влучень при п'яти пострілах) протилежні один одному, тому
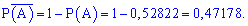
Всі завдання умови виконані і з пояснень є що взяти для кожного з Вас.
Приклад 2. Монету підкидають п'ять разів. Знайти ймовірність того, що герб випаде не більше трьох разів.
Розв'язок. Ймовірність випадання гербу чи решки вважаємо незалежною подією з ймовірністю p=q=0,5. По аналогії з попередньою задачею, шукана ймовірність рівна сумі трьох наступних
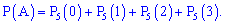
Щоб не шукати стільки доданків, з наведених вище формул отримаємо простішу
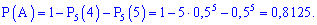
Така ймовірність більша 81%.
Приклад 3. Імовірність появи події в одному досліді рівна 0,4.
Скільки потрібно провести дослідів, щоб найімовірніша кількість появи події була рівна 20.
Розв'язок. Згідно умови виписуємо дані
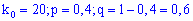
та проводимо розрахунки за нерівністю
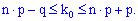
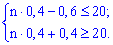
З нерівностей отримаємо
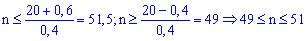
три числа 49,50,51. Отже потрібно провести від 49 до 51 досліду.
Приклад 4. Три біатлоністи незалежно один від одного роблять по одному пострілу в мішень.
Ймовірність попадання в мішень для першого рівна 0,9; для другого – 0,85; для третього – 0,8.
Знайти ймовірність того, що буде закрито дві мішені з трьох.
Розв'язок. Імовірності влучання для стрілків різні, тому застосовуємо твірну функцію.
Для неї вхідні дані приймуть заначення
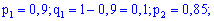
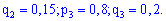
Після підстановки та рокладу в ряд за степенями змінної отримаємо
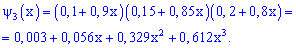
Шукана ймовірність входить в розклад множником при другому степені x2
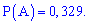
З цього прикладу також легко переконатися, що сума всіх множників при степенях  рівна повній ймовірності (одиниці).
рівна повній ймовірності (одиниці).
Задача1. Садівником восени посаджено 80 саджанців яблунь. Ймовірність того, що саджанець навесні оживе, дорівнює 0,8.
Знайти ймовірність того, що тільки 10 саджанців не розпустять листя навесні.
Розв'язання: Найточніше значення ймовірності знайдемо за формулою Бернуллі
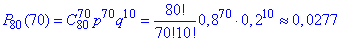
Але при великій кількості незалежних випробувань Ви не зможете скористатися формулою Бернуллі, оскільки калькулятор таких степенів чи факторіалів не обчислить, лише мат. пакети.
Тому для наближених обчислень використовують локальну формулу Лапласа
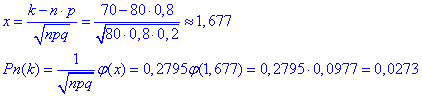
Тут φ(х) значення функції Лапласа.
Порівнянням результатів 0,0277 то 0, 0273, отриманих наведеними способами можете переконатися, що розходження невеликі.
Задача 2. Стрілець здійснює 90 пострілів у мішень. Ймовірність влучення у мішень внаслідок одного пострілу дорівнює 0,82. Знайти ймовірність того, що стрілець влучить у мішень 65 разів.
Розв'язання: Маємо серію n=90 повторних незалежних пострілів, ймовірність влучання в кожному рівна p=0,82, промаху – q=1-0,82=0,18.
Точне значення дає формула Бернуллі
P90(65)=C9065•p65•q(90-65)=90!/(65!•25!)•0,82^65 •0,18^25≈0,007.
Ми як завжди громіздкі обчислення вчимо Вас виконувати в мат. пакетах, зокрема Мейпл комбінації обчислюємо функцією binomial(90,65):
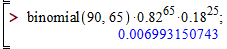
На практиці Вас вчать в таких ситуаціях користуватися локальною теоремою Лапласа, вона дає наближену ймовірність, тому самостійно перевірте розходження в обчисленнях.
Схема Бернуллі на практиці не складна, важливо вловити як в обчисленнях реалізувати завдання типу "не більше m раз", "не менше m раз", "рівно m раз" із n випробувань. Як тільки Ви це зрозумієте, все решта зведеться до сумування, множення та піднесення до степеня.
]]>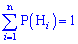 , відомі або можливо встановити апріорні ймовірністі P(Hi) кожної з гіпотез та умовні ймовірності P(A/Hi) події A за умови, що здійснилася та або інша гіпотеза, тоді ймовірність події A визначається за формулою повної ймовірності:
, відомі або можливо встановити апріорні ймовірністі P(Hi) кожної з гіпотез та умовні ймовірності P(A/Hi) події A за умови, що здійснилася та або інша гіпотеза, тоді ймовірність події A визначається за формулою повної ймовірності:
де P(Hi)– ймовірність гіпотези Hi;
P(A/Hi)– умовна ймовірність події 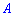 при виконанні гіпотези Hi. Наведена формула називається формулою повної ймовірності.
при виконанні гіпотези Hi. Наведена формула називається формулою повної ймовірності.
Задачі на повну ймовірність
Задача 1. В магазині три холодильники, в яких закінчується морозиво. У першому - 4 білих морозива і 6 шоколадних, у другому - 2 білих і 8 шоколадних, у третьому - 3 білих і 7 шоколадних. Навмання вибирають холодильник і виймають з нього морозиво, визначити ймовірність того, що воно біле.
Розв'язування. Позначимо події наступним чином: Hi – вибрано i-й холодильник, A – вибрано біле морозиво.
Тоді ймовірності витягнути з кожного холодильника однакові і рівні 1/3
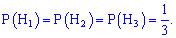
Ймовірності витягнути біле морозиво будуть рівні кількості морозива в кожному з холодильників розділеній на загальну кількість морозива
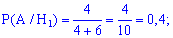
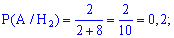
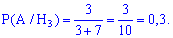
Тут Вам має бути усе зрозуміле.
Використовуючи формулу повної ймовірності, знаходимо
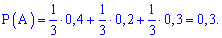
Таким чином ймовірність витягнути біле морозиво рівна 0,3 або 30%.
Задача 2. В офісі є чотири ноутбуки виготовлених компаніює A, 6 компанією B, 8 компаніює C та два, які виготовляє D. Гарантії, що ноутбуки цих компаній працюватимуть протягом гарантійного терміну без ремонту становлять 70 %, 80%, 85%, та 55% для кожної з них. Потрібно знайти ймовірність того, що вибраний ноутбук працюватиме без ремонту протягом гарантійного терміну.
Розв'язування. Позначимо події наступним чином: Hi – вибрано ноутбук компанії;
A – ноутбук працюватиме без ремонту.
Ймовірності вибору ноутбуків кожної з компаній вважаємо рівні їх кількості - на основі цього ймовірності приймуть значення :
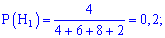
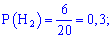
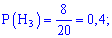
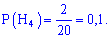
Такі прості обчисення повинен навчитися вионувати та бачити кожен студент.
Ймовірності, що вони працюватимуть без ремонту беремо з умови
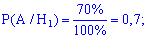
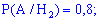
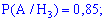
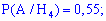
Тут ми просто переводимо проценти в ймовірності.
Застосовуємо формулу повної ймовірності:
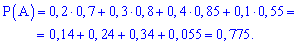
Таким чином, ймовірність безремонтної роботи ноутбука рівна 0,775. Колись це значення можливо було великим досягненням, в теперішній час, якщо б 22,5% ноутбуків потребували ремонту під час гарантійного терміну - це буа б велика проблема виробників.
ФОРМУЛА БАЙЄСА
Нехай гіпотези Hi(i=1,...,n) утворюють повну групу несумісних подій (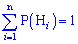 ) і нехай подія A відбувається обов'язково з однією з гіпотез Hi. Нехай подія A відбулася, тоді ймовірність того, що вона відбулася саме за умови Hi визначається формулою Байєса:
) і нехай подія A відбувається обов'язково з однією з гіпотез Hi. Нехай подія A відбулася, тоді ймовірність того, що вона відбулася саме за умови Hi визначається формулою Байєса:
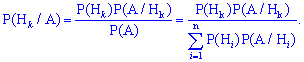
Розглянемо практичну сторону застосування формули Байєса.
Задача 3. Задані умови першої задачі. Потрібно встановити ймовірність того, що морозиво витягнули з другого холодильника.
Розв'язування. Випишемо результати першої задачі, які потрібні для обчислень
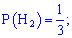
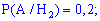
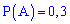
та підставимо у формулу Байєса
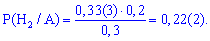
Як можна бачити, такі обчислення не складні, головне зрозуміти, що і як визначається.
Задача 4. Для другої задачі потрібно встановити ймовірності того, що справний ноутбук належить до компаній C та D.
Розв'язування. Випишемо попередньо знайдені ймовірності
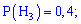
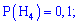
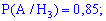
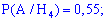
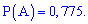
та застосуємо формулу Байєса
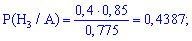
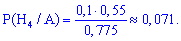
Добре розберіться чому саме так, далі буде важче.
Задача 5. На склад надходять телефони трьох заводів, причому частка телефонів першого заводу становить 25%, другого – 60%, третього – 15%. Відомо також, що середній відсоток телефонів з браком для першої фабрики становить 2%, другої – 4%, третьої – 1%. Знайти ймовірність того, що:
а) навмання взятий телефон виявиться з браком;
б) телефон виготовлений на першому заводі, якщо він бракований;
в) на якому заводі найвірогідніше був виготовлений телефон, якщо він якісно зроблений?
Розв'язування. Проаналізуємо ожне із завдань, щоб Ви якомого краще навчилися розбиратися в формулах.
а) Введемо для ясності позначення:
A – навмання вибраний телефон виявився бракованим;
Припущення: H1 – телефон виготовлений на першій, H2 – другій та H3 – третій фабриках відповідно.
Гіпотези є попарно несумісними і утворюють повну групу. Ймовірність кожного припущення визначаємо діленням процентної частки продукції до всієї (100%)
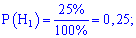
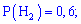
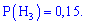
Це не важко знайти для більшості задач теорії ймовірностей..
Подібним чином визначаємо умовні ймовірності шуканої події A
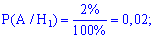
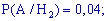
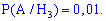
Застосуємо формулу повної ймовірності для визначення можливості вибору бракованого телефону
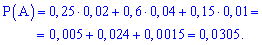
Ймовірність трохи більша за три сотих.
б) для відшукання ймовірності припущення H1 за умови, що подія A виконалася застосуємо формулу Байєса
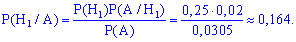
Таким чином, маючи попередні розрахунки, провести обчислення досить просто.
в) щоб визначити, на якому заводі найвірогідніше був виготовлений нормальний телефон, необхідно порівняти між собою ймовірності кожного з припущень :
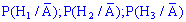
де 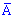 подія (витягнули телефон без браку) протилежна до події A. Для протилежних подій використовують формулу
подія (витягнули телефон без браку) протилежна до події A. Для протилежних подій використовують формулу
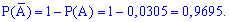
За подібною формулою визначаємо умовні ймовірності події 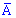 , за умови що справедливі припущення H1, H2, H3
, за умови що справедливі припущення H1, H2, H3



За формулою Байєса обчислюємо ймовірності
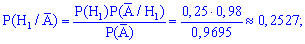
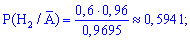
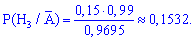
Найбільшу імовірність має друге припущення, тому телефон виготовлено на другому заводі.
Приклад 6. У першій урні 2 білих та 6 чорних куль, у другій – 4 білих та 2 чорних. З першої урни навмання переклали 2 кулі в другу, після чого з другої урни навмання дістали одну кулю.
а) Яка ймовірність того, що ця куля біла?
б) Куля, взята з другої урни, виявилася білою.
Яка ймовірність того, що з першої урни в другу були перекладені 2 білі кулі?
Розв'язування: Результат вибору кульки залежить від того, які кулі переклали.
1) переклали два білі ⇒ у другому кошику стало 6 білих та 2 чорних.
p=6/8 – ймовірність вийняти білу кулю
2) переклали два чорні ⇒ у другому кошику стало 4 білих та 4 чорних.
p=4/8 – ймовірність вийняти білу кулю
3) переклали один білий та один чорний ⇒ у другому кошику стало 5 білих та 3 чорних.
p=5/8 – ймовірність вийняти білу кулю.
Це напряму випливає з того, які набори кульок отримали в другій урні.
Записуємо події - гіпотези:
H1–"переклали дві білих"
H2–"переклали дві чорні"
H3–"переклали чорну, білу"
H4-"переклали білу, чорну".
Ймовірність гіпотез залежить від кількості мячів того чи іншого кольору, тому
p(H1)=2/8*1/7=2/56;
p(H2)=6/8*5/7=30/56;
p(H3)=p(H4)=6/8*2/7=12/56.
Гіпотези утворюють повну групу подій
p(H1)+p(H2)+p(H3)+p(H4)=1.
Подія A-"з другого кошика витягнуто білу кулю":
Випишемо скільки яких куль стало в другій урні та ймовірності події
6 б і 2 ч p(A/H1)=6/8;
4 б і 4 ч p(A/H2)=4/8;
5 б і 3 ч. p(A/H3)=5/8;
5 б і 3 ч p(A/H4)=5/8.
Тоді за формулою повної ймовірності маємо:
p(A)=2/56·6/8+30/56·4/8+12/56·5/8+12/56·5/8=9/16
б) за формулою Байєса знаходимо ймовірність, що взята куля була в другій урні:
p(H2/A)=p(A/H2)*p(H2)/p(A)=30/56·4/8:(9/16)=10/21.
Відповідь: 10/21.
Приклад 7. В спеціалізовану лікарню поступають в середньому 50% з захворюванням А, 30% - В, 20% - С. Ймовірність повного вилікування для А становить 0,7, В - 0,8, С -0,9. Пацієнта виписано здоровим.
Яка ймовірність того, що він хворів В?
Розв'язування: Задача на повну ймовірність та формулу Байєса.
Так як в умові задано захворювання А, В, С, так і позначимо гіпотези.
Тоді їх ймовірності рівні
p(A)=50%/100%=0,5;
p(B)=30%/20%=0,3;
p(C)=20%/100%=0,2.
Тоді ймовірності видужання D за гіпотез рівні:
p(D/A)=0,7;
p(D/B)=0,8;
p(D/C)=0,9.
Знайдемо спершу ймовірність, що пацієнта виписано здоровим:
p(D)=0,5*0,7+0,3*0,8+0,2*0,9=0,77.
Тоді ймовірність, що він хворів В рівна:
p(B/D)=p(D/B)*p(B)/p(D)=0,8*0,3/0,77≈0,31
Відповідь: 0,31.
Задач на знаходження повної ймовірності та застосування формули Байєса в літературі та інтернеті безліч. Варто ввести в гуглі потрібний запит і вам тут же буде запропоновано гори матеріалів до вибору. Тож засвоїти даний матеріал не важко, варто лише уважно (без паніки) розібратися з наведеними прикладами та аналогічні до них. Всі подібні вирішуються за приведеною схемою. Залишайтеся з нами і Ви знатемете більше, ніж розраховували!
]]>
p(A/Bn) - називають умовними ймовірностями (ймовірність події A за умови Вn)
Замість наведеної вище формули ви можете зустріти таку

Вони ідентичні, різниця лише в тому як Вас вчать.
формула Байєса. Ймовірність що подія А відбулась за гіпотези Вn рівна вкладу p(Bn)*p(A/Bn) в ймовірності події A:

Формула Байєса дозволяє переоцінити ймовірності гіпотез після того, як буде відомим результат випробування, внаслідок якого з'явилась подія А.
Далі перейдемо до практичних, але спершу зауважимо одну маленьку деталь, на якій наголошують не всі викладачі. «Утворюють повну групу несумісних подій» означає, що одна з подій від іншої не залежить, і що сума їх ймовірностей рівна 1, тобто
p(B1)+p(B2)+…+p(Bn)=1.
Якщо ця умова не виконується, то група подій не є повною.
Приклад 1. Ймовірність, що айфон куплять в першому магазині дорівнює 0,75, в другому – 0,25. Якщо куплять в першому магазині, то ймовірність отримати в бонус безпровідні навушники рівна 20%, якщо в другому – 60%. Знайти ймовірність того, що при покупці айфону отримають в подарок навушники. Переоцініть ймовірність того, що айфон куплений в першому магазині, якщо при покупці в бонус дали безпровідні навушники. Відповідь запишіть в процентах.
Розв'язування: Позначимо через B1 подію – айфон куплять в першому магазині, B2 – в другому.
Тоді ймовірності P(B1)=0.75, P(B2)=0.25.
Подія А полягає в тому, що до телефону в подарок дадуть навушники.
Тоді умовні ймовірності рівні
P(A/B1)=20%/100%=0.2
P(A/B2)=0.6.
За формулою повної ймовірності знаходимо P(A):
P(A)=P(A/B1)•P(B1)+P(A/B2)•P(B2)=0.75*0.2+0.25*0.6=0.3
Для переоцінки ймовірності, що айфон куплений в першому магазині, якщо бонусом дали безпровідні навушники скористаємося формулою Байєса
P(B1/A)=P(A/B1)•P(B1)/P(A)=0.75*0.2/0.3=0,5.
Відповідь: 30%, 50%.
Приклад 2. В момент початку рейсу може бути сухо з іймовірністю 80%, або піде дощ з імовірністю 20%. Автобус заносить на поворотах з ймовірністю 10% в суху погоду і з ймовірністю 60% під час дощу. Переоцініть імовірність того, що рейс розпочався в суху погоду, якщо автобус заносило на поворотах.
Розв'язування: Дану задачу спершу важко було віднести до формули Байєса, але вона такою є.
Ключовою тут є подія, що автобус заносило, а вже знайти потрібно ймовірність, що заносило в суху погоду.
Позначимо А – подія, що автобус заносило.
H1, H2 гіпотези, що сухо або падає дощ.
Тоді
p(H1)=80%/100%=0.8,
p(H2)=0.2.
Ймовірності події A за умов гіпотез рівні
p(A/H1)=10%/100%=0,1 p(A/H2)=0.6.
Тоді ймовірність, що автобус заносило рівна
p(A)=p(A/H1)•p(H1)+p(A/H2)•p(H2)=0.1*0.8+0.6*0.2=0.2
Переоцінити ймовірність, що рейс розпочався коли було сухо, якщо автобус заносило, означає знайти P(H1/A).
За формулою Байєса отримаємо
P(H1/A)=p(A/H1)•p(H1)/p(A)=0.1*0.8/0.2=0.4
Це і є переоцінка події A.
Відповідь: 0,4.
Приклад 3.До магазину надходять однотипні вироби з трьох заводів, причому перший завод постачає 60%, другий - 30%, третій - 10%. Серед виробів першого заводу 85%, другого - 70%, третього - 80% першосортних. Купуємо один виріб, він виявляється першосортним. Знайти ймовірність того, що придбаний виріб випущений третім заводом.
Розв'язування: Позначимо через B, C, D - гіпотези, що виріб виготовлений першим, другим та третім заводом відповідно.
Тоді ймовірності, що вибрана деталь виготовлена на кожному заводі рівні:
p(B)=60%/100%=0,6;
p(C)=30%/100%=0,3;
p(D)=10%/100%=0,1.
Переконуємося, що гіпотези становлять повну групу подій:
p(B)+ p(C)+p(D)=0,6+0,3+0,1=1.
Нехай подія A полягає в тому, що навмання вибраний виріб першосортний.
Тоді ймовірність такої події в залежності на якому заводі він виготовлений рівна:
p(A/B)=85%/100%=0,85;
p(A/C)=70%/100%=0,7;
p(A/D)=80%/100%=0,8.
за формулою повної ймовірності знаходимо вірогідність, що вибраний виріб першосортний:
p(A)=p(A/B)•p(B)+p(A/C)•p(C)+p(A/D)•p(D)=0,6*0,85+0,3*0,7+0,1*0,8=0,8
Ймовірність того, що першосортний виріб, що вибрали виготовлений третім заводом за формулою Байєса рівна
p(D/A)=p(A/D)•p(D)/p(A)=0,1*0,8/0,8=0,1.
Запам'ятайте цю просту схему обчислень та не забувайте перевіряти (нехай усно) чи гіпотези утворюють повну групу подій.
Відповідь: 0,1.
У Вас умови будуть іншими, тільки якщо зустрінете «Переоцініть ймовірність» знайте, що слід застосовувати формулу Байєса.
]]>