Завдань на формулу Бернуллі, Лапласа, Пуассона в інтернеті безліч, проте не всі вони розкривають відповідь на прості питання:
яку з формул ймовірності і в яких випадах потрібно застосовувати?
Яка похибка формули Лапласа і від чого вона залежить?
Чому в окремих випадках без спрощених формул Пуассона та Лапласа не обійтися?
Дочитайте розв'язки завдань до кінця і Ви отримає усі відповіді на поставлені вище запитання.
Завдання 1 Ймовірність виходу з ладу за час t одного приладу дорівнює p=0.9.
Визначити ймовірність того, що за час t з n=250 приладів вийдуть з ладу:
а) рівно k1=220 приладів;
б) від k2=230 до k3=235 приладів;
в) не менше k4=215 приладів;
г) менше k5=227 приладів.
Значення для кожного варіанту наведені у таблиці, а також продубльовані в умові
Розв'язання: а) Ймовірність, що вийде з ладу рівно 220 приладів з 250 точно можна знайти за формулою Бернуллі
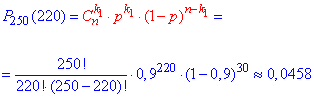
В попередній статті ми показували, як виконувати такі розрахуни в Мейплі.
Для даної теми та інших з теорії ймовірностей старайтеся використовувати одну з програм: Maple, MathCad, Matlab.
Тоді обчислення для будь-яких вхідних значень не таке важке і при великих вхідних значеннях n можна застосовувати формулу Бернуллі.
Запам'ятайте, що вона дає найточніші значення ймовірності і всі решту результати слід звіряти з нею.
Разом з тим в математичних пакетах можна обчислювати наближене значення за допомогою локальної теореми Лапласа.
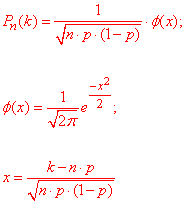
Наведені формули поширені не тільки в ймовірності, але й для опису статистичних процесів.
Властивості функції phi(x) досить легко запам'ятати:
так як маємо експоненту у від'ємному парному степені то функція Лапласа парна,
визначена для всіх дійсних значень змінної
та прямує до нуля, якщо змінна прямує до безмежності.
Це Ви повинні добре знати.
Спершу перевіряємо чи виконується умова n•p•q=250•0,9•0,1=22,5>9, тоді розбіжність зі значенням отриманим за формулою Бернуллі мінімальна.
Чим добуток ближчий до 9, а в окремій літературі вимагають більше 10, тим більше грішить формула Лапласа.
Виконаємо обчислення змінної:
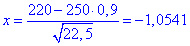
За таблицями табулювання локальної функції Лапласа маємо
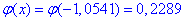
Багато з Вас зразу побачить в цьому пробему - де брати таблиці локальної та інтегральної фунцій Лапласа?
Відповідей декілька:
1. стара схема - шукати в математичному довіднику (при сучасних технологіях листати сторінками і тратити час дорожче для себе);
2. знайти в інтернеті на математичному сайті. В нас їх немає, можете не шукати, але через смартфони чи ноутбуки знайти не проблема.
3. завантажити додаток гугла для ймовірності, їх зараз безліч та вибрати один з готових, який безкоштовно надає широкий функціонал.
4. в любому з мат. пакетів знайти потрібне значення з точністю куди кращою ніж в паперовому довіднику, оскільки там функції протабульовані з певним кроком сітки, а проміжні значення необхідно інтерполювати, що не завжди є просто та займає часу.
Після цього знайти ймовірність можна за формулою
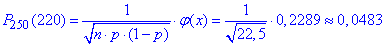
Розбіжність зі значенням отриманим за формулою Бернуллі (p=0.0458) незначне!
б) Ймовірність, що від 230 до 235 приладів із 250 вийдуть з ладу знайдемо за інтегральною формулою Лапласа: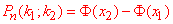 
де
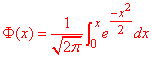- інтегральна функція Лапласа;
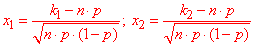- аргументи інтегральної функції розподілу.
Інтегральна формула Лапласа працює коли потрібно знайти ймовірність з немалого проміжку при велиих n. Запам'ятайте це.
Вона дає можливість швидко оцінити ймовірність не виконуючи при цьому велиих за часом обчислень.
Уявіть собі, що тут потрібно шукати (235-230+1)=6 доданків за формулою Бернуллі, при цьому скорочувати факторіали, або імовірність p підносити до високого (>200) порядку степеней.
Для студентів це непідйомне завдання як і для інженерів, тому в давнину були придумані такі формули як Лапласа та Пуасона.
Зараз вже є високоточні компютери та математичні пакети, які все це швидко рахують з наперед заданою точністю.
Ми ж дотримуємося теорії і знаходимо точки "ікси"
А далі через значення інтегральної функції Лапласа в них значення ймовірності.
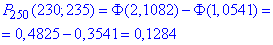
За формулою Бернуллі точне значення рівне 0.1625773175.
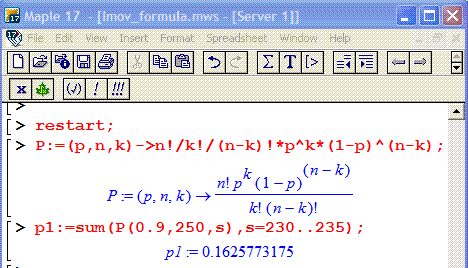
Наведемо Вам фрагмент розрахунків ймовірності в Мейплі.
Ми лише створимо функцію та використаємо бібліотечну функцію суми
restart;
P:=(p,n,k)->n!/k!/(n-k)!*p^k*(1-p)^(n-k);
> p1:=sum(P(0.9,250,s),s=230..235);
p1 := 0.1625773175
Це весь код, який нам необхідний для знаходження точного значення ймовірності.
А тепер задумайтеся для чого Ви ходите на пари, та чи багато нового Вас навчить теперішня "вища" освіта?
Щоб Вас переконати, що більш нічого ми не робили наводимо скріншот мейпла
в) Ймовірність, що не менше 215 приладів зі 250 вийдуть з ладу обчислимо за інтегральною теоремою Лапласа:
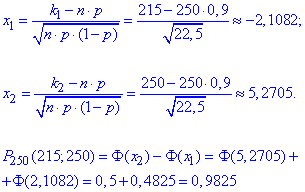
Точне значення обчислене в мейплі через формули Бернуллі рівне
p:= 0.9830960304
г) Ймовірність, що менше 227 приладів вийдуть з ладу означає, що від 0 до 227.
Без спрощених формул на аудиторному занятті таке завдання не рішити (потрібно шукати 228 імоверностей через формулу Бернуллі)
Тому знову скористаємося інтегральною теоремою Лапласа:
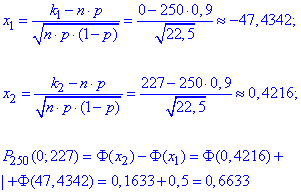
Ми ж нічим не обмежені, тому без труднощів визначаємо точне значення
p= 0.6936836956
Для цього було просумовано 228 доданків.
Порівнюючи отримане точне та наближене значення робимо висновок, що теореми Лапласа дають достатньо добрі значення для оцінки ймовірності.
Завдання 2 Ймовірність виходу з ладу за час t одного приладу дорівнює p=0.9.
Визначити ймовірність того, що за час t з n=500 приладів вийдуть з ладу:
а) рівно k1=7 приладів;
б) від k2=1 до k3=5 приладів;
в) не менше k4=4 приладів;
г) менше k5=3 приладів.
Розв'язання: а) Ймовірність, що вийде з ладу рівно 50 приладів з 90 найточніше можна знайти за формулою Бернуллі
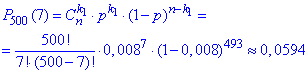
Якщо обчислювати швидко то наближене значення дає локальна теорема Пуассона.
Оскільки k=n•p•q=500•0.008=4<10, то похибка формул мінімальна
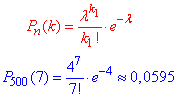
Похибка з точним значенням 0.0594 невелика.
Зверніть увагу, що для використання формули Пуасона необхідно, щоб добуток n•p•q був менший 10.
Для цього ймовірність p повинна приймати значення близькі до нуля.
Для Лапласа навпаки, тому у студентів виникає плутанина, чи можна - чи ні користуватися спрощеними формулами.
Тому що порушення умови веде до занижених або завишених значень ймовірності.
б) Ймовірність, що від 1 до 5 приладів із 500 вийдуть з ладу, знайдемо за теоремою Пуассона для k2=1 і k3=5 та формулою імовірності протилежної події
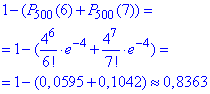
Точне значення рівне
p=0.7677368032
Розбіжність більша, це плата за наближені обчислення.
в) Ймовірність, що не менше 4 приладів із 500 вийдуть з ладу обчислимо, як протилежну подію до того, що з ладу вийдуть менше 4 приладів, тобто або 0, або 1, або 2, або3:
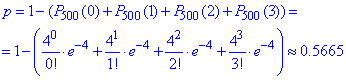
Точне значення імовірності
p=0 .5673147532
Маємо задовільну збіжність.
г) Ймовірність, що менше 3 приладів вийдуть з ладу означає, що від 0 до 3:
Обчислюємо за інтегральною теоремою Пуассона:
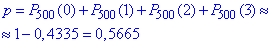
Завдання 3 Ймовірність виходу з ладу за час t одного приладу дорівнює p=0.55.
Визначити ймовірність того, що за час t з n=90 приладів вийдуть з ладу:
а) рівно k1=50 приладів;
б) від k2=45 до k3=55 приладів;
в) не менше k4=47 приладів;
г) менше k5=49 приладів.
Розв'язання: а) Точне значення ймовірності, що вийде з ладу рівно 50 приладів з 90 знаходимо за формулою Бернуллі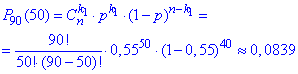 
Наближене значення знаходимо за локальною теоремою Лапласа.
Умова k= n•p•q=90•0.55•0.45=22,275>10 виконується, отже похибка наступних формул мінімальна
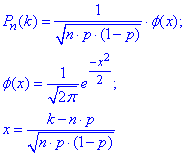
Виконаємо обчислення "ікса":
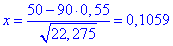
За таблицями табулювання локальної функції Лапласа маємо значення "phi"
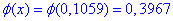
Ймовірність рівна 0.0841
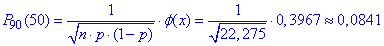
Похибка обчислень мінімальна.
б) Ймовірність, що від 45 до 55 приладів із 90 вийдуть з ладу знайдемо за інтегральною формулою Лапласа: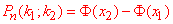
де
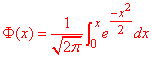- інтегральна функція Лапласа;
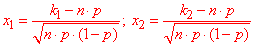- аргументи інтегральної функції розподілу.
Знаходимо "ікси" функції Лапласа, а далі за таблицею значення інтегральної функції в точках та саму ймовірність
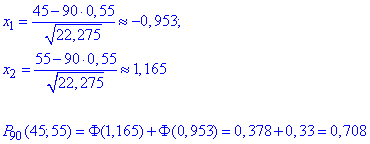
За точною формулою
p:=0 .7539348193
в) Ймовірність, що не менше 47 приладів зі 90 вийдуть з ладу обчислимо за інтегральною теоремою Лапласа: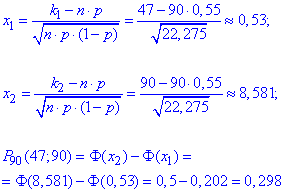 
Формули легко читати, проте вони приховують масу обчислень, які необхідні для отримання правильної відповіді.
г) Ймовірність, що менше 49 приладів вийдуть з ладу означає, що від 0 до 48 знходимо за інтегральною теоремою Лапласа:
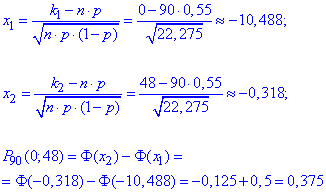
Точне значення p:=0.4148530245, розбіжність більша ніж потрібно.
Останні два приклади, які ми підготували разом з калькулятором на формули Лапласа в мейплі будуть розглянуті в наступній публікації.
