Всім студентам хто навчається у ВУЗах на факультетах з поглибленим вивченням математичних дисциплін дана стаття стане доброю інструкцією та навчить застосовувати формулу Бернуллі там де це необхідно.
Далі наведено готові відповіді всього навсього до 5 прикладів, причому ми не стали змінювати умову. Вона стала від завдання до завдання, міняються лише змінні в умовах. Проте, якщо дочитаєте до кінця - знатимете для чого потрібна формула Бернуллі, та в яких випадках вона працює.
Задача 1 Ймовірність хибного виклику пожежної команди (подія A) p=p(A)=0.8.
Яка ймовірність, що серед n=19 викликів число хибних викликів буде:
- а) рівно k1=9 разів;
- б) від k2=7 до k3=10 разів;
- в) хоча б один раз;
- г) не менше k4=17 разів;
- д) обчислити найімовірніше число хибних викликів.
Розв'язання: а) Оскільки ймовірність не залежить від історії (попередніх дослідів), то за формулою Бернуллі знаходимо
б) Ймовірність, що хибних викликів буде від 7 до 10 серед 19 також знайдемо за формулою Бернуллі через суму відповідних значень
в) «Хоча б один раз» рівносильно від 1 до 19 – це є протилежною подією до жодного хибного виклику. Чому саме так читайте в поясненнях до 5 прикладу.
г) «Не менше 17 разів» означає або 17, або 18, або 19 (формула Бернуллі)
д) Найімовірніше число хибних викликів знайдемо з умови:
Найімовірніше, що буде 15 хибних викликів.
Така ймовірність рівна
Це короткі пояснення головних моментів, щоб більш детально розібратися з окремими нюансами просимо дочитати статтю до кінця.
Формула Бернуллі в Мейпл
З розрахунів Ви могли зауважити, що обчислення та спрощення факторіалів, піднесення чисел до високих показників можливе із застосуванням інженерних калькуляторів. Однак світ рухається вперед і на сьогодні це вже не актуально.
В інтернеті чимало онлайн розв'язників та скриптів, які виконують обчислення за Вас.
Достатньо мати смартфон з підключеним інтернетом, та бажання знайти все це в інтернеті.
Проте з цього Ви нічого не навчитеся, лише вирішите проблему.
Інша ідея, яку ми пропагуємо на сайті - це вивчення та застосування математичних пакетів скрізь де це моживо, економить час, вимагає точності.
Давайте напишемо разом простенький код, який виконує наведені вище обчислення на автоматі. Все що на нашу думку буде Вам новим ми детально прокоментуємо.
> restart; занулюємо всі змінні, які були до цього введені в Мейплі.
Створююємо функцію, яа знаходить імовірність за формулоб Бернуллі
> P:=(p,n,k)->n!/k!/(n-k)!*p^k*(1-p)^(n-k);
Далі переходимо до розрахунку імовірностей, що:
що серед n=19 викликів число хибних викликів буде рівно 9 разів
> p1:=P(0.8,19,9);
У відповідь отримаємо
p1 := 0.001269633565
Ймовірність, що хибних викликів буде від 7 до 10 серед 19 усіх знаходимо тричі застосувавши формулу Бернуллі
> p2:=P(0.8,19,7)+P(0.8,19,8)+P(0.8,19,9)+ P(0.8,19,10);
p2 := 0.006651148560
Але це ще не ефетивний код. Уявімо собі, що потрібно знайти ймовірність, що якась подія виникне від 40 до 60 разів зі 100.
Ви ж не будете писати стільи доданків, це нереально.
Тому далі поажемо як це зробити в циклі
> p2_1:=0:
> for k from 7 by 1 to 10 do
> p2_1:=p2_1+P(0.8,19,k) end do;
В результаті отримаємо перше значення та суму попереднього з наступним
p2_1 := 0.00004328296243
p2_1 := 0.0003029807370
p2_1 := 0.001572614302
p2_1 := 0.006651148560
Остатнє і буде шуаною імовірністю.
Але це ще не все, можна все це записати одним рядом, застосувавши функцію сумування в Мейпл.
> p2_2:=sum(P(0.8,19,s),s=7..10);
p2_2 := 0.006651148559
Імовірність, що хибний викли буде хоча б один раз знаходимо із залежності
> p3:=1-(1-0.8)^19;
p3 := 1.
Як бачите, значення настільи близьке до одиниці, що для Мейпла це одне і те саме.
Імовірність, що хибних виликів буде "Не менше 17 разів" знаходимо за формулою суми
> p4:=sum(P(0.8,19,s),s=17..19);
p4 := 0.2368893404
Далі знаходимо інтервал в який попадає найімовірніше число хибних викликів
> n1:=19*0.8-(1-0.8); n2:=19*0.8+(1-0.8);
n1 := 15.0
n2 := 15.4
В цей інтервал попадає найменше ціле яе рівне 15.
Далі знаходимо ймовірність, що з 19 викликів рівно 15 будуть хибними.
> p5:=P(0.8,19,15);
p5 := 0.2181994019
Фрагмент вікна програми із знайденими за формулою Бернуллі імовірностями наведено на рисунку
Цей код не ідеальний, оскільки вирішує лише 1 завдання.
Ми могли б дати Вам готовий код, який лише за даними таблиці розраховує усі ймовірності.
Але це надто простий шлях. Хто займається розрахуновими, модулями з теорії ймовірності обов'язово захоче довести наведены обчислення до автоматизму, повірте що це під силу кожному.
Для візуалізації розрахунків Вам також підійде MathCad, Matlab непоганий пакет для роботи з числами, матрицями, однак у ньому, на відміну від двох згаданих солверів, відсутня візуалізація формул.
Тому вибирайте практичний з точки зору використання мат. пакет та поступово вчіться використосовувати в розрахунках.
Задача 2 Ймовірність хибного виклику пожежної команди (подія A) p=p(A)=0.7.
Яка ймовірність, що серед n=18 викликів число хибних викликів буде:
- а) рівно k1=8 разів;
- б) від k2=6 до k3=9 разів;
- в) хоча б один раз;
- г) не менше k4=16 разів;
- д) обчислити найімовірніше число хибних викликів.
Розв'язання: а) Тут у всіх завданнях ймовірність не залежить від історії, в кожному новому досліді хибний виклик може настати з наперез заданою в умові частотою.
Тому формула Бернуллі дає нам шукану імовірність
б) Ймовірність, що хибних викликів буде від 6 до 9 серед 18 також знайдемо за формулою Бернуллі
в) "Хоча б один раз" еквівалентно від 1 до 18 – це є протилежною подією до жодного хибного виклику
P=1-(1-p)n=1-(1-0.7)18=0.9999
г) "Не менше 16 разів" означає або 16, або 17, або 18 (формула Бернуллі)
P18(16)+P18(17)+P18(18)=0.0599
д) Найімовірніше число хибних викликів знайдемо з нерівності:
Отримаємо інтервал з якого найімовірніше, що буде 13 хибних викликів. Така ймовірність рівна
При 12 хибних викликах ймовірність буде близька, але менша. В цьому рекомендуємо Вам переконатися самостійно.
Задача 3 Ймовірність хибного виклику пожежної команди (подія A) p=p(A)=0.8.
Яка ймовірність, що серед n=20 викликів число хибних викликів буде:
- а) рівно k1=4 разів;
- б) від k2=3 до k3=5 разів;
- в) хоча б один раз;
- г) не менше k4=19 разів;
- д) обчислити найімовірніше число хибних викликів.
Розв'язання: а) Першу ймовірність знаходим одноразовим застосуванням формули Бернуллі 
б) Ймовірність, що хибних викликів буде від 3 до 5 серед 20 також знайдемо за формулою Бернуллі 
в) "Хоча б один раз" рівносильно від 1 до 20 , що є протилежною подією до жодного хибного виклику.
Комусь, мабуть, надоїли повторення з прикладу в приклад тих самих пояснень, але це єдиний дієвий та перевірений спосіб, щоб у Вас в голові пояснення відклалися та трималося хоч короткий проміжок часу
P=1-(1-0.8)20=0.9999
г) "Не менше 19 разів" означає або 19, або 20 з 20. Розраховуємо імовірності та сумуємо
д) Найімовірніше число хибних викликів знайдемо з умови:
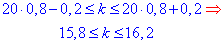
Пошук найменшого цілого значення з інтервалу показує, що найімовірніше буде 16 хибних викликів.
Така ймовірність рівна 0.22
Задача 4 Ймовірність хибного виклику пожежної команди (подія A) p=p(A)=0.7.
Яка ймовірність, що серед n=19 викликів число хибних викликів буде:
- а) рівно k1=5 разів;
- б) від k2=2 до k3=4 разів;
- в) хоча б один раз;
- г) не менше k4=18 разів;
- д) обчислити найімовірніше число хибних викликів.
Розв'язання: а) Оскільки ймовірність не залежить від історії (попередніх дослідів), то за теоремою Бернуллі отримаємо
б) Ймовірність, що хибних викликів буде від 2 до 4 серед 19 також знайдемо за формулою
в) "Хоча б один раз" означає від 1 до 19 , а це в свою чергу є протилежною подією до жодного хибного виклику
P=1-(1-p)n=1-(1-0.7)19=0.9999
г) "Не менше 18 разів" означає або 18, або 19
Як правило викладачі задають значення близькі до кінця проміжку, щоб полегшити Вам обчислення. Шукати 2 доданки за схемою Бернуллі куда простіше, ніж з половини проміжку.
Ніхто б не обчислював, навіть на калькуляторі, якщо б в умові стояло не менше 10 разів.
В таких випадках без математичних пакетів не обійтись і це я думаю кожен розуміє.
Однак в освіті цього не помічають і до сьогоднішньго дня всі шукають по 2, 3 доданки з розкладу і роблять вигляд, що це важкі задачі з ймовірності.
д) Найімовірніше число хибних викликів знайдемо з умови:
Найменше ціле значення з інтервалу 13, тому найвірогідніше, що буде саме стільки хибних викликів.
Далі знаходимо яка при цьому буде ймовірність
Задача 5 Ймовірність хибного виклику пожежної команди (подія A) p=p(A)=0.95.
Яка ймовірність, що серед n=16 викликів число хибних викликів буде:
- а) рівно k1=8 разів;
- б) від k2=1 до k3=3 разів;
- в) хоча б один раз;
- г) не менше k4=15 разів;
- д) обчислити найімовірніше число хибних викликів.
Розв'язання: а) Знаємо, що ймовірність подій не залежить від історії (попередніх дослідів), тому за формулою Бернуллі обчислюємо
б) Ймовірність, що хибних викликів буде від 3 до 5 серед 20 також знайдемо за формулою Бернуллі
в) "Хоча б один раз" еквівалентно від 1 до 16 – це є протилежною подією до жодного хибного виклику. Справа в тому, що нормальний розподіл визначається за формулою Бернуллі.
Сума ймовірностей, що хибних викликів буде від 0 до 16 рівна одиниці. Тому замість шукати ймовірності, що буде 1 хибний виклик, 2, 3 і т.д. можна піти іншим шляхом. Знайти імовірність, що хибних викликів не буде.
Далі від одиниці відмінусовуємо це значення і отримаємо суму решту членів ряду.
P=1-(1-p)n=1-(1-0.95)16=0.9999
г) "Не менше 15 разів" означає що від 15 до останнього номера - 16 (формула Бернуллі)
д) Найімовірніше число хибних викликів знайдемо з умови:
Тут теорія дає збій і на інтервалі немаємо цілого значення, тому наближчим цілим до інтервалу є 15 (хибних викликів).
Ймовірність, що буде саме стільки рівна
Дякуємо за потрачений час, сподіваємося Ви знайшли відповіді на питання з якими потрапили на сайт.
Уважно перегляньте сусідні сторінки категорії, ми підібрали для Вас чимало потрібних для навчання тем, що дозволяють в повній мірі освоїти поширені розділи теорії ймовірностей.
