ЗНО математика. Задачі з комбінаторики

Шановні школярі, випускники, абітурієнти, цей розділ допоможе підготуватися до зовнішнього незалежного оцінювання з математики 2017 року. Відповіді до тестів допоможуть засвоїти теоретичний матеріал та методику обчислень, систематизувати та підвищити накопичений рівень знань з математики.

Розділ IV. Елементи комбінаторики, початки теорії ймовірностей та елементи статистики

Завдання 4.1 - 4.9 мають по п'ять варіантів відповідей, із яких тільки одна правильна. Правильно виконане завдання оцінюється 1 балом.

Задача 4.1 У коробці шість однакових кубиків, які занумеровані числами від 1 до 6. По одному витягають усі кубики. Знайдіть імовірність того, що номери витягнутих кубиків з'являться у порядку зростання.
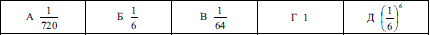ЗНО тести Розв'язання: В теорії ймовірностей на задачах з комбінаторики побудовані всі складні теореми і виведення формул, тому хто добре розбереться з простими задачами – Комбінаторика, як і сама Теорія ймовірності не складна.
Для прикладу, проаналізуємо дану задачу – кубик з цифрою 1 можна витягнути в 1 із 6 варіантів, тобто ймовірність першим витягнути кубик з цифрою 1 рівна 1/6. Після цього залишиться 5 кубиків з номерами від 2 до 5. Ймовірність з цієї кількості витягнути кубик з номером 2 рівна 1/5. Відповідно, ймовірність вибрати третій з цифрою 3 – 1/4 і так далі.
Сумарна ймовірність витягнути кубики в порядку зростання рівна добутку ймовірностей

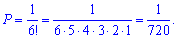
Ймовірність 1/720 відповідає варіанту А тестових відповідей.
Відповідь: А.

Задача 4.2 (Т-07, 33) З натуральних чисел від 1 до 30 учень навмання називає одне. Яка ймовірність того, що це число є дільником числа 30?
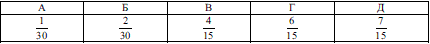ЗНО тести Розв'язання: Аналізуємо умову – задано 30 чисел, випишемо в ряд дільники числа 30.
1;2;3;5;6;10;15;30.
Їх кількість рівна 8
N=8.
Щоб знайти ймовірність ділимо кількість сприятливих подій до загальної кількості можливих
P=8/30=4/15.
Отримана відповідь наведена в варіанті В ЗНО тестів, і може добавити 1 бал на тестуванні.
Відповідь: В.

Задача 4.3 У коробці лежать різнокольорові кульки, з яких 40 - червоні, 20 - коричневі, а всі, що залишилися - жовті. З'ясуйте, скільки жовтих кульок лежить у коробці, якщо ймовірність вибору випадковим чином жовтої кульки дорівнює 0,75.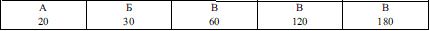
ЗНО тести Розв'язання: До прикладу з комбінаторики потрібно скласти рівняння. Ймовірність витягнути жовту кульку серед N всіх кульок рівна
P(A)=0,75.
Кількість червоних і коричневих рівна
40+20=60.
З іншої сторони ця ймовірність обчислюється з рівняння

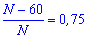
Розв'язавши його, ми знайдемо загальну кількість кульок, а також зможемо обчислити кількість жовтих
N-60=0,75*N;
N(1-0,75)=60;
0,25*N=60;
N=60/0,25=240 – кількість усіх кульок.
Далі обчислюємо скільки серед знайдених жовтих
n=N-60=240-60=180.
Результат відповідає варіанту Д ЗНО тестів.
Відповідь: Д.