Шановні школярі, випускники, абітурієнти, цей розділ допоможе підготуватися до зовнішнього незалежного оцінювання з математики у 2017 року. Відповіді до тестів допоможуть Вам зрозуміти матеріал та методику обчислень, систематизувати та підвищити накопичений рівень знань з математики.
Розділ III. Функції
В завданнях 3.46 - 3.62 правильна відповідь оцінюється 2 балами.
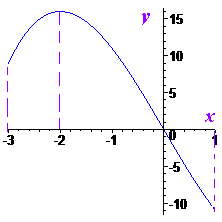
Завдання 3.55 Знайдіть найбільше значення функції f(х) = х3 - 12х на відрізку [-3; 1].
Розв'язання: Обчислимо похідну функції
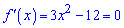
І з умови, що похідна рівна нулю знайдемо стаціонарні точки
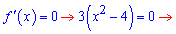
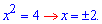
Обчислюємо значення функції на краях проміжку та в точці екстремуму
x=-2 f(-3)=-27+12*3=36-27=9;
f(-2)=-8+12*2=24-8=16;
f(1)=1-12=-11.
Максимум функції рівний 16.
Відповідь: 16.
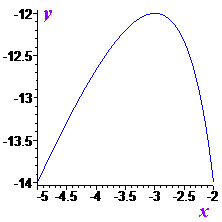
Завдання 3.56 Знайдіть найбільше значення функції
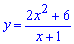
на відрізку [-5; -2]
Розв'язання: Хочете Ви цього чи не хочете, а без похідної перевірити функцію на стаціонарні точи не вийде. Тому за формулами диференціювання обчислюємо похідну від частки
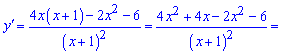
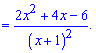
Знаменник нас не цікавить, а от чисельник прирівнюємо до нуля і розв'язуємо квадратне рівняння
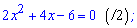
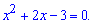
За теоремою Вієта розкладемо на прості множники
(x+3)(x-1)=0; x=-3; x=1.
Далі обчислюємо значення функції у точках, що належать проміжку
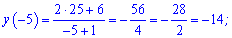
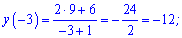
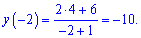
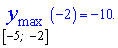
Помилку допускають ті хто вважає, що -14 є більшим за -10.
Відповідь: -10.
Залишайтеся з нами і підготовка до ЗНО з математики залишиться для Вас приємним спогадом та зекономить багато часу та грошей на репетиторів.
Відповіді до ЗНО тестів
- ЗНО відповіді з математики
- Попередня стаття - ЗНО 2017 математика. Найбільше значення функції на проміжку
- Наступна стаття - ЗНО 2017 математика. Завдання на похідну