ЗНО математика. Найбільше значення функції на проміжку

Шановні школярі, випускники, абітурієнти, цей розділ допоможе підготуватися до зовнішнього незалежного оцінювання з математики у 2017 року. Відповіді до тестів допоможуть Вам зрозуміти матеріал та методику обчислень, систематизувати та підвищити накопичений рівень знань з математики.

Розділ III. Функції

В завданнях 3.46 - 3.62 правильна відповідь оцінюється 2 балами.

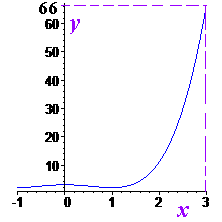
Завдання 3.53 Знайдіть найбільше значення функції f(х) = х⁴ - 2х² + 3 на відрізку [-1;3].
Розв'язання: Перевіримо чи має функція точку максимуму на проміжку. Для цього обчислимо похідну

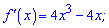
Та прирівняємо її до нуля

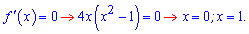
Функція має дві точки локального екстремуму, отже потрібно шукати значення функції в 4 точках – в знайдених + краї проміжку. Виконуємо обчислення
f(-1)=1-2+3=2
В одиниці за рахунок парності функції значення теж 2.
f(0)=3;
f(3)=81-27+3=57.
Максимум функції досягається на краю проміжку і рівний 57.
Щоб можна було уявити функцію наводимо її графік

графік функції
В нулі маємо локальний максимум, однак його не так легко помітити через масштаб графіка.
Відповідь: 57.

Завдання 3.54 (Т-07, 31) Знайдіть найбільше значення функції у = х³- 3х² + 2 на проміжку [-1; 1].
Розв'язання: Схему обчислень максимумів та мінімумів функції на проміжку Ви повинні знати. Спершу перевіряємо чи має функція стаціонарні точки на заданому проміжку. Обчислюємо похідну

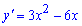
та прирівнюємо її до нуля
3x(x-2)=0; x=0; x=2.
Знаючи критичні точки знаходимо значення функції на краях проміжку та в 0.
y(-1)=-1-3+2=-2 y(0)=2 ;

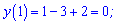
Максимум досягається в точці локального екстремуму

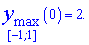
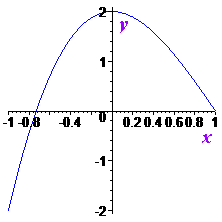
Графік функції має вигляд