ЗНО математика. Діагональ, площа

Шановні школярі, випускники, абітурієнти, цей розділ допоможе підготуватися до зовнішнього незалежного оцінювання з математики 2015 року. Відповіді до тестів допоможуть засвоїти теоретичний матеріал та методику обчислень, систематизувати та підвищити накопичений рівень знань з математики.

Розділ V. Планіметрія

Задача 5.1 - 5.32 мають по п'ять варіантів відповідей, із яких тільки одна правильна. Правильно виконане завдання оцінюється 1 балом.

Задача 5.7 Чотирикутник АВСD - паралелограм. Відомо, що АВ = 1 см, ВС = 2 см, < A=60. Знайдіть діагональ ВD.
ЗНО тести Розв'язання: Виконаємо побудову паралелограма 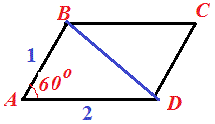З малюнку бачимо, що діагональ паралелограма можна обчислити за теоремою косинусів

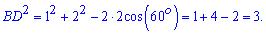
Знаходимо корінь квадратний

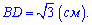
Варіант Б є відповіддю до тесту.
Відповідь:B

Задача 5.8 (Т-06, 47) У прямокутнику АВСD прямі m і n проходять через точку перетину діагоналей. Площа фігури, що складається з трьох зафарбованих трикутників, дорівнює 12 см² . Обчисліть площу прямокутника АВС .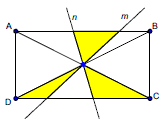
ЗНО тести Розв'язання: Для обчислень потрібно знати, що діагоналі прямокутника ділять його на 4 трикутники однакової площі. Зафарбований вгорі сектор доповнює нижній трикутник по площі, а весь прямокутник рівний площі трикутника помноженій на 4.
S=4*12=48 (сантиметрів квадратних).
Варіант Д є відповіддю до тесту.
Відповідь: Д.

Задача 5.9 (Т-07, 76) Точка М - середина сторони квадрата АВСD. Площа зафарбованої частини дорівнює 7 см². Знайдіть площу всього квадрата. 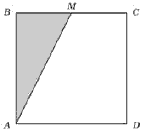ЗНО тести Розв'язання: З побудови бачимо, що площа зафарбованої частини є половиною від половини, або четвертою частиною всього квадрата. Повну площу квадрата знаходимо множенням на 4.
4*7=28 (сантиметрів квадратних).
Варіант В є правильним.
Відповідь: B.
Задача 5.10 У трапеції АВСD основи ВС і АD відносяться як 1:3. Знайдіть площу трапеції, якщо площа трикутника ВСD дорівнює 2 см² .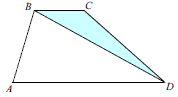 ЗНО тести Розв'язання: Нехай Ви не знаєте як розв'язати дану задачу, спробуйте обійти умову на основі певних міркувань. Задано лише, що основи відносяться як 1/3. Значить співвідношення,яке виражає площу трапеції універсальне відносно її вигляду. Для простоти побудуємо прямокутну трапецію зі сторонами при прямому куті 3 і 2. Менша основа трапеції рівна один.
Тоді площа трапеції рівна пів сумі основ помноженій на висоту або
S=(1+3)/2*2=4.
Площа трикутника рівна
S₁=2*3/2=3.
Площа заштрихованої частини трапеції відповідно рівна
S-S₁=4-3=1.
На основі цього можна скласти пропорцію

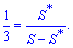
Де S* - заштрихована площа трапеції. З попередніх міркувань слідує, що при такій пропорції повна площа трапеції в 4 рази більша за позначену частину, тобто
S=4*2=8 (сантиметрів квадратних).
Це відповідає варіанту В відповідей.
Є і другий спосіб, але до нього ми додумалися дещо пізніше. Він простий і підійде усім.
Діагональ трапеції розбиває її на два трикутники. Площа кожного рівна пів добутку основи на висоту.
Оскільки висота в них однакова, то відношення площ трикутників у трапеції рівне відношенню основ.
Звідси площа трикутників рівна
S=2+2*3=8 (сантиметрів квадратних).
Результати однакові, а от схема обчислень зрозуміла багатьом.
Відповідь: В.
Залишайтеся з нами і підготовка до ЗНО з математики залишиться для Вас приємним спогадом та зекономить багато часу та грошей на репетиторів.