Шановні школярі, випускники, абітурієнти, цей розділ допоможе підготуватися до зовнішнього оцінювання 2017 року. Відповіді до тестів допоможуть Вам зрозуміти матеріал та методику обчислень, систематизувати та підвищити накопичений рівень знань з математики.
Розділ II. Рівняння і нерівності
Завдання 2.1 -2.36 мають по п'ять варіантів відповідей, із яких тільки одна правильна. Правильно виконане завдання оцінюється 1 балом.
Завдання 2.7 (Т-07, 29) Укажіть, скільки дійсних коренів має рівняння х3 - 4|х| = 0.

Розв'язання: Схема обчислень полягає в наступному - розкриваємо модуль і знаходимо корені, які належать інтервалам
x>0; x^3-4x=0;
x=0; x=-2; x=2.
x<0; x^3+4x=0;
x(x^2+2)=0; x=0.
Отримали два корені x=2; x=0, що відповідає варіанту В ЗНО тестів.
Відповідь: В.
Завдання 2.8 Корінь рівняння
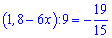
дорівнює:
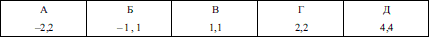
Розв'язання: Приведемо дробове рівняння до вигляду
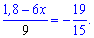
Використовуючи пропорції перетворимо рівняння до вигляду
1,8-6*х=-(19*9/15)=-( 19*3/5)=-(57/5)=-11,4
та знайдемо корінь
6х=1,8+11,4=13,2;
х=13,2/6=2,2.
З відповідей до тестів підходить варіант Г.
Відповідь: Г.
Завдання 2.9 Розв'яжіть нерівність
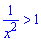
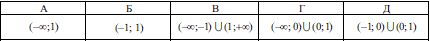
Розв'язання: Виписуємо умову на область допустимих значень. Переносимо одиницю за знак нерівності і зводимо під спільний знаменник
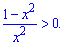
Нулями чисельника є точки x=1; x=-1. крім цього функція є парною, отже області будуть симетричними відносно осі Oy. Підстановкою числа, наприклад двійки, переконуємося, що розв'язком є інтервали.
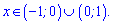
Розв'язок нерівності відповідає варіанту Д тестів.
Відповідь: Д.
Залишайтеся з нами і підготовка до ЗНО 2015 з математики залишиться для Вас приємним спогадом та зекономить багато часу та грошей на репетиторів.
Відповіді до ЗНО тестів
- ЗНО 2017 відповіді з математики
- Попередня стаття - ЗНО 2017 математика. Рівняння і нерівності
- Наступна стаття - ЗНО 2017 математика. Нерівності


