Розберемо готові відповіді до завдань на знаходження M(X), D(X), σ(X) неперервної випадкої величини X.
Формули математичного сподівання, дисперсії та середнього квадратичного відхилення
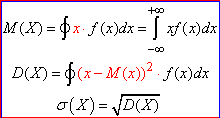
Приклад 1. Для якого значення k функція f(x)=k*exp(-(x^2+4x+4)) є щільністю розподілу випадкової величини Х?
Знайти M(X), D(X), σ(X) і обчислити
P(-4<X<-2.9).
Розв'язання: Задана щільність розподілу змінюється за експоненціальним законом, тому визначена на всій дійсній осі. Щоб вона мала властивості щільності розподілу необхідно, щоб інтеграл по всій множині значень (x∈R) був рівним одиниці (int(f(x),x)=1). Цю умову ще називають нормалізацією щільності розподілу. Вона потрібна для того, щоб ймовірність повної події не перевищувала одиницю. Невизначений інтеграл без мат. Пакету Ви навряд чи знайдете, бо він рівний функції erf(x)
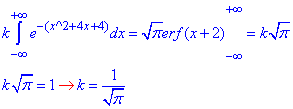
Далі, визначивши k, обчислюємо інтегруванням числові характеристики розподілу та ймовірність попадання в інтервал
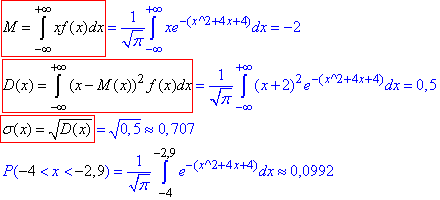
На цьому всі потрібні числові характеристики обчислено, використовуйте наведені алгоритми на практичних та екзаменах.
Приклад 2. Задано функцію розподілу F(x) неперервної випадкової величини X:
F(x)=0
F(x)=(x^3+2x)/12, x∈(0;2] ;
F(x)=1, x>2.
Знайти щільність розподілу f(x) і числові характеристики M(x), D(x), σ(x).
Розв'язання: Щільність розподілу знаходимо диференціюванням функції розподілу
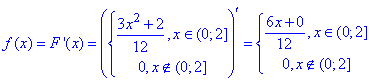
Слід пам'ятати, що функція розподілу заданана кусково неперервною функцією, тому щільність розподілу рівна нулю скрізь де щільність приймає стале значення.
Отже f(x)=0,5х, x∈(0;2] і f(x)=0 за межами інтервалу.
Щоб знайти математичне сподівання домножимо щільність розподілу на «ікс» і проінтегруємо на проміжку, де вона приймає відмінні від нуля значення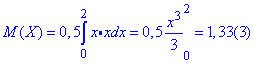
Через інтеграл знаходимо дисперсію.
Для цього інтегруємо щільність домножену на множник, який рівний (x-M(X))^2.
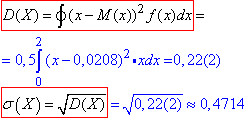
Середнє квадратичне відхилення це корінь з дисперсії.
Наведемо фрагмент коду з мат. пакету Мейпл

Приклад 3. Щільність розподілу випадкового вектора (X,Y) має вигляд f(x,y)=(3x+y)/7, x∈[0;2], y∈[0;1] і f(x,y)=0 в інших випадках.
Знайти середнє квадратичне відхилення складової Y.
Розв'язання: Для обчислення σ(X) нам потрбно знайти дисперсію D(Y), а в її формулу входить математичне сподівання M(Y).
Тому інтегруванням знаходимо одну величину за іншою, спершу матем. сподівання
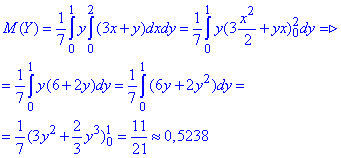
Далі обчислюємо дисперсію та середнє квадратичне відхилення
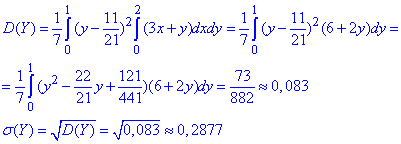
Повний інтеграл дисперсії розпишіть самостійно, ми ж взяли результат з обчислень в мейплі.
Для інтегрування служить функція int().
Математичне сподівання в мейплі можна обчислити так:
>My:=int(y*int((3*x+y),x=0..2),y=0..1);
Далі його копіюємо в другий рядок і змінюємо множник y перед внутрішнім інтегралом на (y-My)^2:
>Dy:=int((y-My)^2*int((3*x+y),x=0..2),y=0..1);
>sigma_y:=Dy^0.5;
Щоб обчислити кожен рядок проходимо командою «Enter» і отримаємо результат
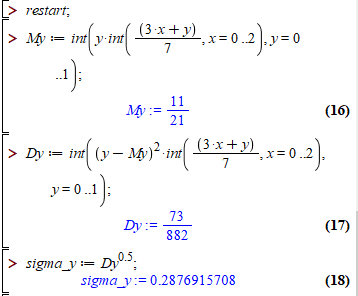
Це куди швидше, аніж по пів уроку тягнути інтеграл. Подібним чином виглядає код і в MatLab, в MathCad потрібно трохи повозитися з іконками. При теперішньому темпі розвитку ніхто на роботі не буде Вас заставляти інтегрувати вручну, максимум в мат. пакетах, або за допомогою команд в програмах, які автоматично підраховують вказані величини.
Приклад 4. Щільність розподілу ймовірностей випадкового вектора (X,Y) має вигляд f(x,y)=(2y-x)/12, якщо x∈[0;2], y∈[0,3] і рівна нулю f(x,y)=0 за межами інтервалів. Знайти математичне сподівання M(XY).
Обчислення:Математичне сподівання від добутку M(XY) обчислюємо інтегруванням щільності ймовірностей, домноженої на xy: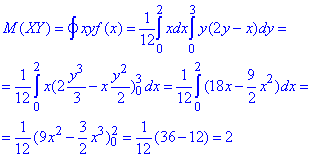
Отримали М(XY)=2.
З уроки Ви повинні запам'ятати, що інтеграл щільності розподілу по області рівний одиниці (умова нормування)+ вивчити формули числових характеристик для неперервної випадкової величини X. Все решта зводиться до інтегрування, яке Ви повинні вміти виконувати перед вивченням цієї теми.


