Розглянемо теоремe Чебишева, що присвячена граничним законам розподілу. Нехай задано ξ випадкову величину, що характеризується математичним сподіванням Мξ та дисперсією Dξ.
Теорема 1. Імовірность відхилення випадкової величини ξ від її математичного сподівання за модулем не менше будь-якого додатного числа ε, що не перевищує Dξ/ε^2.
Інше формулювання: Для випадкової величини X із математичним сподіванням Мξ і дисперсією Dξ можна вибрати будь-яке ε>0, для якого виконується нерівність:
Приклад 2.1 Відомо, що дисперсія кожної з заданих незалежних випадкових величин не перевищує C. Визначити кількість таких величин, при яких ймовірність абсолютної величини відхилення середнього арифметичного випадкових величин від середнього арифметичного їх математичних сподівань не більше, ніж на ε перевищує 0,99.
C=5; ε=0,2.
Розв'язування: Нехай ξ - незалежна випадкова величина; n - кількість таких величин.
За умовою задачі:
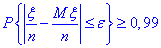– ймовірність того, що ймовірність абсолютної величини відхилення середнього арифметичного випадкових величин від середнього арифметичного їх математичних сподівань не більше, ніж на ε перевищує 0,99, де
ξ /n - середнє арифметичне випадкових величин;
Mξ /n - середнє арифметичне їх математичних сподівань.
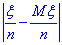- абсолютної величини відхилення середнього арифметичного випадкових величин від середнього арифметичного їх математичних сподівань.
Скористаємось ІІ нерівністю Чебишова:
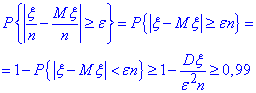
Тут знак в формулі стоїть ≥, оскільки віднімаємо значення з нерівності Чебишева ≤.
Отримали нерівність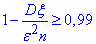 
, де Dξ =C=5, ε=0,2.
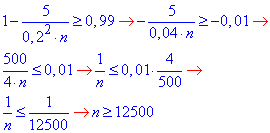
Кількість незалежних випадкових величин, що задовольняють умові завдання більше, ніж 12500.
Відповідь: n≥12500.
Приклад 2.2 Добова витрата електроенергії для персональних потреб у населеному пункті становить в середньому 4000 кВтˑгод. Оцінити ймовірність того, що протягом найближчої доби витрата електроенергії у населеному пункті не перевищить 10000 кВтˑгод.
Розв'язування: Нехай випадкова величина ξ – це добова витрата електроенергії, тоді Mξ=4000 – математичне сподівання цієї величини.
Скористаємось І нерівністю Чебишова:
За умовою задачі треба оцінити ймовірність того, що протягом найближчої доби витрата електроенергії у населеному пункті не перевищить 10000 кВтˑгод (тут a=10000), тобто
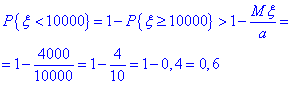
отже P{ ξ <10000}>0,6.
Зазначимо, що тут використано властивість ймовірності протилежної події P{ξ <a}=1- P{ξ ≥a}, а також властивості рівносильних нерівностей:
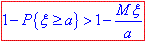рівносильна 
.
Отже, протягом найближчої доби витрата електроенергії у населеному пункті не перевищить 10000 кВтˑгод за ймовірністю не менше 0,6 (P>0,6).
Відповідь: P>0,6.
З кожним роком поступає більше задач з екзаменів та практикумів з теорії ймовірностей та математичної статистики на нерівності Чебишева, тому з такими задачами Вас будемо ознайомлювати. А Вас просимо ділитися готовими відповідями зі всіми студентами через наш сайт!
