Перед тим як розкладати вектор за базисом виконують перевірку – чи утворюють вектори базис. Якщо ні то немає змісту шукати через них розклад певного вектора.
Якщо маємо тримірний простір то достатньо трьох векторів, що не лежать в одній площині, щоб всі інші вектори можна було виразити через лінійну комбінацію трьох (a,b,c).
Не всі вектори простору можуть бути базисом, тому й виконують перевірку –
якщо визначник складений з векторів відмінний від нуля, то вектори утворюють базис;
якщо ранг матриці, побудованої на векторах рівний розмірності простору, то вектори лінійно незалежні, отже утворюють базис.
Далі наведені типові приклади на перевірку "чи утворюють вектори базис?" та наприкінці кілька завдань з параметром.
ЗАВДАННЯ 1 Перевірити, чи утворюють базис вектори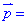 
(0,1,2), 
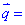(1,2,-1), 
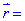(1,0,-5)
Розв'язання: Для перевірки складемо з векторів матрицю
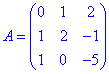
та перевіримо чи її ранг рівний 3.
Якщо rang=3, то вектори лінійно незалежні і вони утворюють базис.
Як шукати ранг матриці Ви повинні знати, якщо ні то дивіться статтю.
Альтернативою є обчисення визначника побудованого на векторах.
Ящо детермінант відмінний від нуля, то вектори утворюють базиc.
Якщо detA=0 то вектори лінійно залежні (не утворюють базису).
Знайдемо визначник матриці, розклавши його через алгебраїчні доповнення до першого стовпця
detA=-1•(-5+0)+1•(-1-4)=0.
Визначник рівний нулю, тому робимо висновок, о вектори не утворюють базис в просторі.
ЗАВДАННЯ 2 Довести, що вектори p(0,1,2), q(1,0,1), r(-1,2,4) утворюють базис.
Розв'язання: Доведемо, що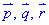 
утворюють базис: Знайдемо ранг матриці, попередньо звівши матрицю складену із векторів до трикутного виду
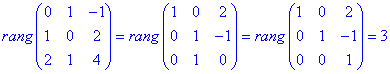
rang=3 або визначник матриці
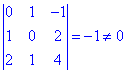
detA=-1 – відмінний від нуля.
Система векторів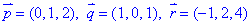 
лінійно незалежна, а тому задані вектори утворюють базис.
ЗАВДАННЯ 3 Чи утворюють базис вектори 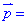(5, 1, 0), 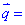(2, -1, 1), 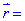(1, 0, -1)?
Розв'язання: Вионаємо перевірку рангу матриці
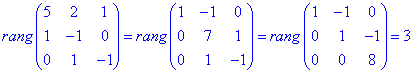
або визначника матриці
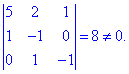
Необхідні умови існування базису виконуються, отже вектори лінійно незалежні.
На практиці вибирайте одну перевірку з двох – або знаходите визначник, або ранг матриці з векторів.
Обидва варіанти в плані обчислень рівносильні.
ЗАВДАННЯ 4 Довести, що вектори 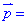(0, 1, 2), 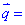(1, 0, 1), 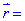(-1, 2, 4) утворюють базис.
Розв'язання: Складемо матрицю з векторів та знайдемо її ранг
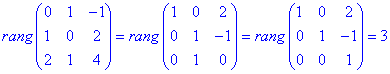
Оскільки rang=3, то задана система векторів утворює базис.
ЗАВДАННЯ 5 Довести, що вектори 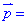(4,1,1), 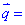(2,0,3), 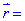(-1,2,1) утворюють базис.
Розв'язання: Обчислюємо ранг матриці з векторів
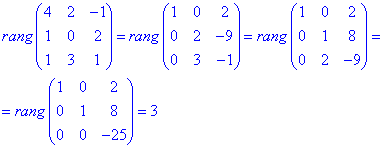
rang=3, отже вектори лінійно незалежні та утворюють базис.
ЗАВДАННЯ 6 Перевірити чи вектори 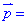(1,0,2), 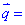(0,1,1), 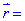(2,-1,4) утворюють базис.
Розв'язання: Будуємо на векторах матрицю та знаходимо її визначник
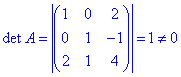
Детермінант =1 (не рівний нулю), отже система векторів лінійно незалежна, а тому задані вектори утворюють базис.
ЗАВДАННЯ 7 Довести, що вектори a(1,0,5), b(-1, 3, 2), c(0,-1,1) утворюють базис.
Розв'язання: Складемо матрицю з векторів, а далі, методом зведення до східчастого вигляду переконаємося, що rangA=3:
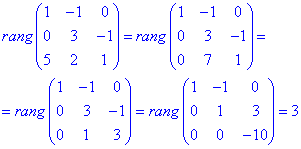
Умова базису виконується, вектори лінійно незалежні.
ЗАВДАННЯ 8 Довести, що вектори a(1,1,0), b(0,1,-2), c(1,0,3) утворюють базис.
Розв'язання: Складаємо з векторів матрицю та знаходимо її визначник
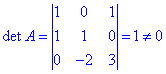
detA=1, отже вектори утворюють базис.
ЗАВДАННЯ 9 При якому значенні параметра a вектори (2,1,1), (-1,1, 2), (1,3,b) будуть лінійно залежними?
Розв'язання: Схема обчислень наступна: складаємо з векторів матрицю та знаходимо її визначник.
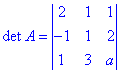
detA=2a+2-3-1+a-12=3a-14.
Далі прирівнюємо його до нуля та визначаємо, який параметр задовільняє цій умові
detA=0;
3a-14=0;
a=14/3.
При a=14/3 вектори будуть лінійно залежними.
ЗАВДАННЯ 10 При якому параметрі a вектори (3,2,1), (a,3,-2), (1,2,2) не утворять базису?
Розв'язання: Алгоритм обчислень наведено в попередньому прикладі. Складаємо матрицю з векторів та обчислюємо визначник.
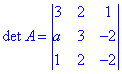
detA=-18-4+2a-3+4a+12=6a-13.
З умови рівності нулю визначника визначаємо невідомий параметр
detA=0;
6a-13=0;
a=13/6.
При a=13/6 вектори не утворюють базис (лінійно залежні).
