"Розкласти функцію в ряд по степенях x" - саме так звучить питання з вищої математики, яке одним студентам під силу, а інші не можуть справитися із завданням. Є кілька способів розкладу ряду, тут буде дана методика розкладу функцій в ряд Маклорена. При розвиненні функції в ряд потрібно добре вміти обчислювати похідні.
Приклад 4.7 Розкласти функцію в ряд по степенях x:
![]()
Обчислення: Розклад виконуємо за формулою Маклорена:
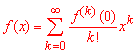
Спочатку розвинемо в ряд знаменник функції,
![]()
а вкінці помножимо розклад на чисельник.
Значення функції в нулі f(0)=1/3.
Знайдемо похідні функції першого та вищих порядків f(x) і значення цих похідних в точці x=0:
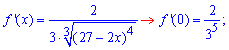
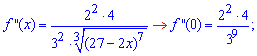
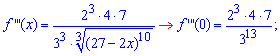
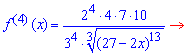
![]()
Далі із закономірності зміни значення похідних в 0 записуємо формулу для n-ї похідної
![]()
Отож, знаменник матиме наступне розвинення в ряд Маклорена
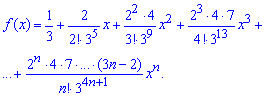
Множимо на чисельник і отримуємо розклад функції в ряд по степенях х
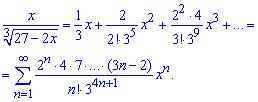
Як бачите нічого складного тут немає.
Всі ключові моменти базуються на вмінні обчислювати похідні і швидкому узагальненні значення похідної старших порядків в нулі. Наступні приклади допоможуть Вам навчитися швидко розкладати функцію в ряд.
Приклад 4.10 Розкласти функцію в ряд по степенях x
![]()
Обчислення: Як Ви можливо здогадалися розкладати в ряд будемо косинус в чисельнику. Для цього можете використати формули для нескінченно малих величин, або ж вивести розклад через похідні. В результаті прийдемо до наступного ряду за степенями x
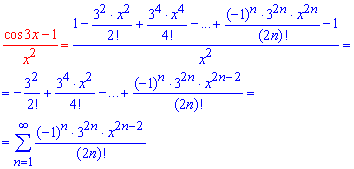
Як бачите маємо мінімум обчислень і компактний запис розкладу через ряд.
Приклад 4.16 Розкласти функцію в ряд по степенях x:
7/(12-x-x^2)
Обчислення: В такого роду прикладах необхідно дріб розкласти до найпростіших дробів.
Як це робити ми зараз не будемо показувати, але за допомогою невизначених коефіцієнтів прийдемо до суми дох дробів.
Далі записуємо знаменники в показниковій формі
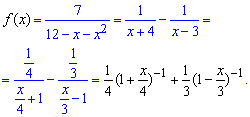
Залишилося розкласти два доданки за допомогою формули Маклорена. Підсумовуючи доданки при однакових степенях "ікс" складаємо формулу загального члена розкладу функції в ряд
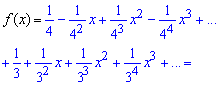
![]()
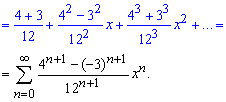
Останню частину переходу до ряду на початках важко реалізувати, оскільки складно об'єднати формули для парних та непарних індексів (степенів), але з практикою у Вас це буде виходити щоразу краще.
Приклад 4.18 Розкласти функцію в ряд по степенях x
![]()
Обчислення: Знайдемо похідну цієї функції:
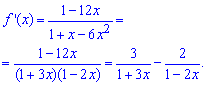
Розкладемо функцію ![]() в ряди, скориставшись однією з формул Маклорена:
в ряди, скориставшись однією з формул Маклорена:
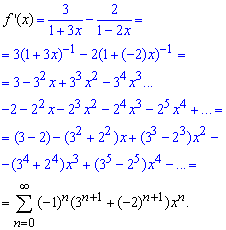
Ряди почленно додаємо на основі того, що обидва абсолютно збіжні. Проінтегрувавши почленно весь ряд, отримаємо розклад заданої функції в ряд по степенях x:
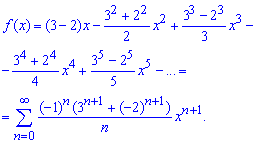
Між останніми двома рядками розкладу є перехід, який на початку у Вас забиратиме чимало часу. Узагальнення формули ряду не всім дається легко, тож не переймайтеся з приводу того, що не можете дістати красивої формули.
Приклад 4.28 Розкласти функцію в ряд по степенях x:
![]()
Запишемо функцію наступним чином
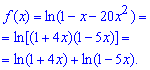
За формулою Маклорена розкладаємо в ряд по степенях x логарифм функцію
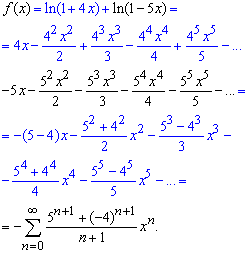
Кінцеве згортання на перший погляд складне, однак при чергуванні знаків Ви завжди отримаєте щось подібне. Вхідний урок з теми розкладу функцій в ряд завершено. Інші не менш цікаві схеми розладу будуть детально розглянуті в наступних матеріалах.
Готові розв'язки на ряди:


