Одним з методів розкладу функції в ряд є обчислення похідної функції, далі похідну розвивають в ряд (формули Маклорена) та інтегруванням знаходять розклад початкової функції. На словах це виглядає дещо заплутано, однак наступні приклади повинні розкрити суть цієї методики.
Приклад 5.8 Розкласти арктангенс функцію в ряд за степенями x:
Обчислення: Напряму розкладати арктангенс я би нікому не радив, тому спершу обчислимо похідну функції:
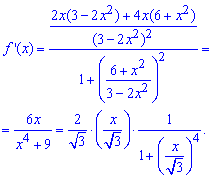
Позначимо за нову змінну 
, тоді похідна матиме компактний запис
Далі знаменник похідної за формулами Маклорена розкладаємо в ряд
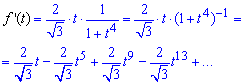
Повертаючись до заміни, отримаємо розклад похідної
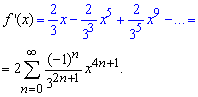
Після цього почленно інтегруємо весь ряд та отримаємо кінцеву формулу розкладу арктангенса
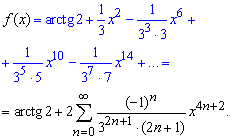
Обчислень багато, але на практиці завдання бувають не легші.
Приклад 5.13 Розкласти арктангенс функцію в ряд за степенями x
Обчислюємо похідну від арктангенса, як від складеної функції
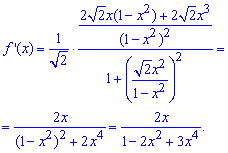
Спрощення дозволяють отримати компактний вираз похідної Далі записуємо розклад похідної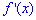 
в ряд з невизначеними коефіцієнтами
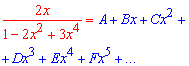
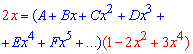
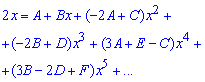
Повної схеми наводити зараз не будемо, однак, якщо перенести знаменник по праву сторону знаку рівності та прирівняти коефіцієнти при однакових степенях x то отримаємо розріджену систему рівнянь і вкінці її розв'язок:
A=0, B=2, C=0,D=4,E=0, F=2, ….
Після цього можемо записати розклад похідної у вигляді
Якщо запис проінтегрувати, то дістанемо розклад функції за степенями x
Формула, незважаючи на складність розрахунків, досить компактна.
Приклад: 5.19 Розкласти арксинус функцію в ряд за степенями x
Обчислення: За наведеною вище схемою спершу знаходимо похідну від складеної функції:
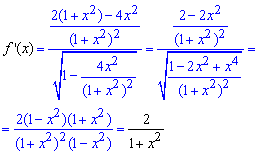
Розкладаємо похідну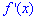 
в ряд за формулою Маклорена
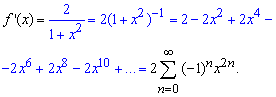
Інтегрування ряду не викликає ніяких труднощів і ми дістаємо фінальний розклад арксинуса в ряд
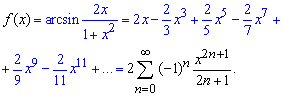
Приклад: 5.29 Розкласти логарифм в ряд по степенях x
Обчислення: Під логарифмом маємо складену функцію, тож за правилом складеної функції за диференціюємо логарифм і множимо на похідну від функції в дужках
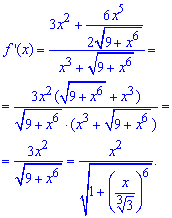
За формулами Маклорена розкладаємо похідну логарифма , а вірніше її знаменник в ряд за степенями x
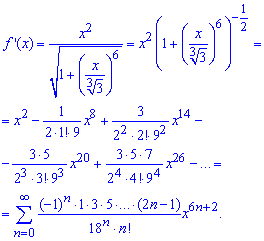
Загальний член ряду містить як показникову так і факторіальну залежність від індексу. Інтегруємо члени ряду, та враховуючи, що f(0)=ln(3), отримаємо розклад логарифма за степенями змінної x
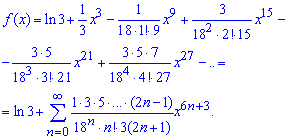
На цьому знайомство з розкладом функції в ряд Маклорена добігає кінця, більше прикладів Ви знайдете за наступними посиланнями.
Готові розв'язки на ряди:
