Неоднорідне диференціальне рівняння третього порядку

Теорію обчислень неоднорідних диференціальних рівнянь (ДР) наводити в даній публікації не будемо, з попередніх уроків Ви маєте достатньо інформації, щоб знати "Як розв'язати неоднорідне диференціальне рівняння?" Степінь неоднорідного ДР тут великої ролі не грає, не так вже і багато є способів, які дозволяють обчислити розв'язок ДР. Щоб Вам було легко читати відповіді до прикладів основний наголос буде зроблено лише на методиці обчислень, та підказках, які полегшать вивід кінцевої функції. Завдання взято з курсу, розробленого для математиків Львівського національного університету ім. І. Франка

Приклад 1. (8.11) Знайти загальний розв'язок диференціального рівняння:
Розв'язання: Задано однорідне диференціальне рівняння (ДР) третього порядку, причому воно містить лише другу та третю похідні, та немає функції та її першої похідної. В таких випадках застосовують метод пониження степеня диференціального рівняння. Для цього вводять параметр – позначимо другу похідну через параметр
,
тоді третя похідна функції рівна
.
Вихідне однорідне ДР спроститься до вигляду

Записуємо його в диференціалах, далі зводимо до рівняння з відокремленими змінними та знаходимо розв'язок інтегруванням

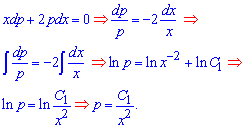
Згадуємо, що параметр це друга похідна функції

тому для знаходження виразу самої функції двічі інтегруємо знайдену диференціальну залежність
.
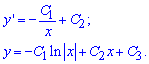В функції сталі C₁, C₂, C₃ – набувають довільних значень.
Ось так просто виглядає схема, що дозволяє знайти загальний розв'язок однорідного диференціального рівняння методом введення параметра. Наступні завдання дещо складніші і з них ви навчитеся розв'язувати неоднорідні диференціальні рівняння такого ж порядку. Між однорідними та неоднорідними ДР в плані обчислень є деяка відмінність, в цьому Ви зараз переконаєтеся.

Приклад 2.(8.14) Знайти загальний розв'язок диференціального рівняння:
Розв'язання: Маємо неоднорідне диференціальне рівняння третього порядку. Тому його розв'язок слід шукати у вигляд суми двох – розв'язку однорідного та часткового розв'язку неоднорідного рівняння
.
Розв'яжемо спершу однорідне диференціальне рівняння:

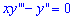
Як бачимо воно містить тільки другу і третю похідну функції і не містить самої функції. Такого сорту диф. рівняння розв'язують методом введення параметра, що в свою чергу понижує та спрощує знаходження розв'язку рівняння. На практиці це виглядає наступним чином: нехай друга похідна рівна певній функції , тоді третя похідна формально матиме запис
.
Розглянуте однорідне диф. рівняння перетвориться до вигляду

звідки заходимо інтеграл рівняння xdp-pdx=0;

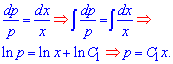
Сталі в таких завданнях лід нумерувати, оскільки розв'язок диф. рівняння 3 порядку матиме 3 сталі, четвертого - 4 і та далі. Тепер повертаємося до введенного параметра – оскільки друга похідна має вигляд , то інтегруючи її один раз маємо залежність для похідної похідної

і повторним інтегруванням знаходимо загальний вигляд самої функції

Частковий розв'язок рівняння запишемо у вигляді змінної помноженої на логарифм. Це слідує з того, що права неоднорідна частина диф. рівняння рівна -1/x і щоб отримати еквівалентний запис

слід розв'язок шукати у вигляді

Знайдемо коефіцієнт A, для цього обчислимо похідні першого та другого порядків

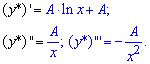
Підставимо знайдені вирази в початкове диференціальне рівняння і прирівняємо коефіцієнти при однакових степенях x:

Стала рівна -1/2, а розв'язок неоднорідного рівняння має вигляд
.
Загальний розв'язок диференціального рівняння записуємо у вигляді суми знайдених

де C₁, C₂, C₃- довільні константи, які можна уточнити з задачі Коші.

Приклад 3. (8.20) Знайти загальний розв'язок диференціального рівняння:
Розв'язання: Шукаємо загальний інтеграл неоднорідного диференціального рівняння третього порядку у вигляді суми розв'язку однорідного та часткового неоднорідного рівняння
.
Спершу для будь-якого типу рівнянь починаємо аналізувати однорідне диференціальне рівняння:

Воно містить лише другу та третю похідні невідомої поки що функції. Вводимо заміну змінних (параметр): позначимо за другу похідну

тоді третя похідна рівна
.
Такі ж перетворення виконували в попередньому завданні. Це дозволяє звести диф. рівняння третього порядку до рівняння першого порядку вигляду

Інтегруванням знаходимо розв'язок однорідного рівняння

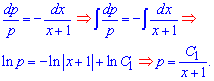
Згадуємо, що відповідно до заміни змінних це тільки друга похідна

а щоб знайти розв'язок однорідного диференціального рівняння третього порядку її потрібно двічі про інтегрувати

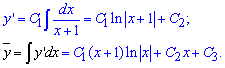
Виходячи з вигляду правої сторони (неоднорідної частини =x+1), частковий розв'язок рівняння шукаємо у вигляді

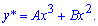
Як знати в якому вигляді шукати частковий розв'язок Вас повинні були навчити в теоретичній часині курсу диференціальних рівнянь. Якщо ні, то можемо лише підказати, що за функцію вибирають такий вираз щоб при підстановці в рівняння доданок, що містить найстаршу похідну або молодшу був одного порядку (подібний) з неоднорідною частиною рівняння

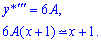
Думаю тепер Вам зрозуміліше, звідки береться вигляд часткового розв'язку. Знайдемо коефіцієнти A,B, для цього обчислюємо другу та третю похідну функції

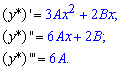
та підставляємо в диф. рівняння. Після групування подібних доданків, отримаємо лінійне рівняння

з якого при однакових степенях змінної складаємо систему рівнянь

та знаходимо невідомі сталі. Після їх підстановки частковий розв'язок рівняння виражається залежністю
.
Загальний розв'язок диференціального рівняння рівний сумі однорідного і часткового та має вигляд

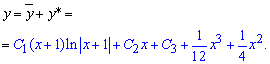
де С₁, С₂, С₃ - довільні константи.

Приклад 4. (8.22) Знайти загальний розв'язок диференціального рівняння:
Розв'язання: Маємо неоднорідне диференціальне рівняння третього порядку, розв'язок якого будемо знаходити через суму двох
.
Схема обчислень Вам відома, тому переходимо до розгляду однорідного диференціального рівняння:

За стандартною методикою вводимо параметр
Вихідне диференціальне рівняння набуде вигляду 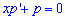, звідки можемо записати інтеграл однорідного рівняння

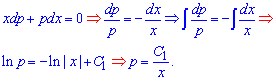
Згадуємо чому рівний параметр – це друга похідна
Інтегруючи диф. рівняння отримаємо першу похідну функції

Повторним інтегруванням знаходимо загальний інтеграл однорідного диференціального рівняння

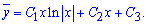
Частковий розв'язок рівняння шукаємо у вигляді , оскільки права частина рівна
Знайдемо коефіцієнт A - для цього підставимо цей вираз в диференціальне рівняння і прирівняємо коефіцієнт при однакових степенях змінної:
,
Після підстановки в рівняння і групування доданків отримаємо залежність

з якої стала рівна A=8/3, звідси
Отож, частковий розв'язок такий
.
Загальний розв'язок диференціального рівняння рівний сумі двох

де С₁, С₂, С₃ - довільні константи.

Вважаю, що матеріал Вам пригодиться при підготовці до практичних занять, модуля чи контрольної. Тут не розбирали задачу Коші, проте з попередніх уроків Ви загалом знаєте як це зробити.