Неоднородное дифференциальное уравнение по сложности вычислений можно разделить на два типа: первый имеет неоднородную функцию, которая не связана с решением однородного уравнения. Второй тип предполагает, что неоднородная часть ДУ может содержать экспоненту, синусы и косинусы или произведения экспонент на синусы и косинусы. Первый из вариантов ДУ подробно рассмотрен на предыдущих уроках. Далее будут проанализированы готовые ответы на сложные неоднородные ДУ 3 порядка: в этой статье задания, содержащие экспоненту, в последующих - тригонометрические функции.
Сразу хочу обратить Ваше внимание что на важных моментах при вычислениях отмечено и их следует заучить или выписать. В общем материал должен Вам понравиться и помочь в учебе!
Как решить неоднородное дифференциальное уравнение?
Пример 1. (10.16) Найти общее решение дифференциального уравнения:
![]()
Решение.Имеем неоднородное дифференциальное уравнение третьего порядка - одно из сложных в данном разделе. Его решение ищем через сумму решений однородного и неоднородно диф. уравнений ![]() . Найдем каждый из корней, для этого выполняем анализ однородного дифференциального уравнения
. Найдем каждый из корней, для этого выполняем анализ однородного дифференциального уравнения
![]()
Его решение ищем в виде суммы экспоненциальных функций
y=exp(k*x).
При подстановке в однородное уравнение и делении на exp(k*x) (всегда больше нуля) получим характеристическое уравнение
![]()
Поскольку уравнение кубическое то один из корней ищем среди простых множителей свободного члена другие два - с неполной квадратного уравнения, которое останется
(k2-1)(k-3)=0.
В результате получим следующие значения
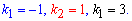
Так как корни характеристического уравнения различны действительные числа то решение имеет вид суммы произведения констант на экспоненты в соответствующих степенях
![]()
Правая часть дифференциального уравнения (4-8x)ex имеет вид полинома умноженного на степенную зависимость экспоненты P(x)ex, причем коэффициент в показательной функции является корнем характеристического уравнения (k=1),поэтому частичное решение запишем в виде
![]()
Определим А и В, входящие в формулу функции. Для этого подставим y в дифференциальное уравнение и приравняем коэффициенты при одинаковых степенях x. Вычисляем производные до третьего порядка
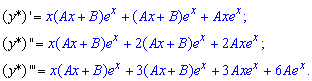
и подставляем в исходное дифференциальное уравнение. После объединения подобных слагаемых получим зависимость
![]()
Отсюда при одинаковых степенях переменной определяем сталые A=1, B=-1.
Таким образом частичное решение ДУ можем записать формулой
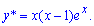
Общее решение дифференциального уравнения находим суммированием функций
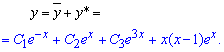
Здесь С1, С2, С3 – сталые, которые принимают произвольные значения. Доопределить их можем только при наличии условия Коши для функции.
Теперь Вы знаете, как решить неоднородное дифференциальное уравнение 3 порядка и как составить характеристическое уравнение.
Пример 2. (10.22) Найти общее решение дифференциального уравнения
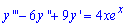
Решение:Решим неоднородное дифференциальное уравнение третьего порядка через суперпозицию двух корней.![]() .
.
Опуская выкладки которые можно прочитать с предыдущей задачи запишем характеристическое уравнение для однородного диф. уравнения и найдем его корни
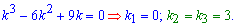
Поскольку два корни одинаковы то общий интеграл однородного ДУ имеет вид
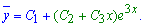
Правая часть данного уравнения 4x*ex имеет вид полинома первой степени P(x) умноженного на экспоненциальную функцию exp(x),поэтому и частичное решение уравнения ищем в таком же виде
![]()
Находим производные до третьего порядка
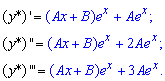
и подставляем в исходное ДУ. После объединения подобных слагаемых получим
![]()
Отсюда находим сталые – А=1; В=0. Можем записать явный вид частного решения ДУ
![]()
Общий интеграл дифференциального уравнения находим как сумму найденных функций
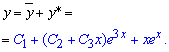
На этом задача решена.
Пример 3.(10.24) Найти общее решение дифференциального уравнения:
![]()
Решение:Корни неоднородного дифференциальное уравнение третьего порядка по известной Вам схеме ищем в виде суммы![]()
Для однородного дифференциального уравнения характеристическое уравнение имеет вид
![]()
Решив его, получим три корня, причем один кратности 2
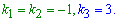
В таких случаях ответ записываем формулой
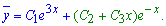
Правая часть неоднородного диф. уравнение -(8x+4)*ex имеет вид P(x)ex, при этом степень экспоненты не совпадает с характеристическими корнями, поэтому в аналогичном виде ищем частичное решение
![]()
Находим производные до третьего порядка
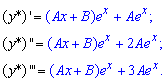
Подставляем их в дифференциальное уравнение и группируем общие слагаемые, в результате получим
![]()
откуда, приравняв коэффициенты при одинаковых степенях аргумента, определяем стали A=1; B=0.
Таким образом частичное решение уравнения можем записать зависимости
![]()
Далее суммированием находим общее решение дифференциального уравнения
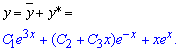
Как можно убедиться из приведенных задач вычисления не слишком сложные. Если есть задачи которые трудно самостоятельно решить - просьба присылать их нам на почту. Мы постоянно ищем и подбираем задачи которые научат Вас нового и в полной мере раскроют тему.
Во время учебы Вам приходилось брать куда сложные производные и интегралы, схема решения неоднородных уравнений довольно простая и ее под силу запомнить каждому.
Чтобы материал Вам лучше запомнился найдите в методичках по которым учитесь похожие дифференциальные уравнения и решите самостоятельно. Поверьте - это намного больше Вам поможет, чем прочитать на сайте и сказать - "Я все понял!". Чтобы потом не было на модули или контрольной вопросов "Как решить неоднородное дифференциальное уравнение?"
И знайте - в случае проблем при решении мы готовы Вам помочь.


