Рiвнянням в повних диференцiалах називається рiвняння вигляду
M(x,y)dx + N(x,y)dy = 0)
лiва частина якого є повним диференцiалом деякої функцiї
F(x,y), тобто,
dF(x,y) = M(x,y)dx + N(x,y)dy
Нагадаємо, що повний диференцiал функцiї F знаходиться за формулою
Умова перевірки рівняння на повний диференціал має вигляд
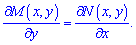(1)
Рівняння звідні до ДР в повних диференціалах
В деяких випадках рівняння
M(x,y)dx + N(x,y)dy = 0
не є рівнянням в повних диференціалах, не виконується умова (1). Однак існує функція "м'ю"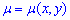 
така, що якщо на неї помножити початкове рівняння 
то отримаємо рівнянням в повних диференціалах.
Необхідною та достатньою умовою цього є рівність часткових похідних
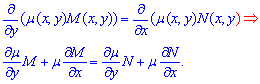
Функція "м'ю" називають інтегруючим множником.
Таким чином окрім ДР відносно функції u(x,y) на практиці приходиться розв'язувати диференціальне рівняння в частинних похідних відносно інтегруючого множника.
Але досі залишається невідоме питання, як його знаходити?
Як знайти інтегруючий множник?
В теорії як правило методика вже розроблена і інтегруючий множник слід шукати у вигляді 
де "омега" 
- відома функція.
В цьому випадку одержуємо
Після підстановки в умову повного диференціалу отримаємо
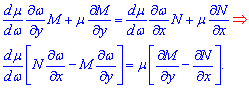Розділимо змінні в останньому рядку
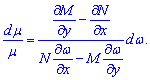Проінтегрувавши і поклавши сталу інтегрування рівною нулю знаходимо інтегруючий множник
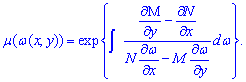Розглянемо часткові випадки.
1) Нехай "омега" рівна аргументу . Тоді деякі часткові похідні рівні нулю , а інтегруючий множник знаходять за формулою
. 
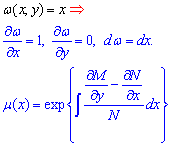2) Якщо "омега" рівна "ігрику", формула обчислення інтегруючого множника має вигляд
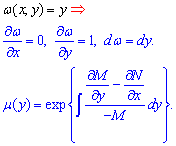3) Випадок, коли "омега" рівна сумі або різниці квадратів змінних. Інтегруючий множник знаходимо за формулою
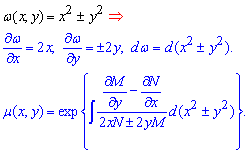4) І варіант коли маємо добуток змінних дає наступну залежність для визначення м'ю
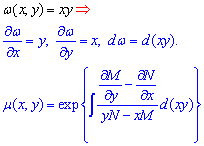Виведення формули інтегруючого чножника бе практики Вас нічого не навчить, тому розглянемо завдання з контрольної на яких Ви побачите суть всіх наведених вище формул. Приклади задавали в Львівському національному університеті ім. І. Франа, тому хто там вчиться готові відповіді зацінять..
Рівняння в повних диференціалах. Задача Коші.
Приклад 1. (7.15) Знайти розв'язок задачі Коші:
Розв'язання: Випишемо множники при диференціалах
і перевіримо чи виконується умова повного диференціалу функції двох змінних
Як бачимо, ліва частина рівняння не є повним диференціалом (умова не виконується). Встановимо, чи не допускає диференціальне рівняння інтегруючого множника:
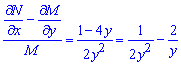
З правої сторони бачимо, що дане рівняння допускає множник інтегрування, причому він залежить тільки від y.
Знайдемо інтегруючий множник з диференціального рівняння з відокремленими змінними
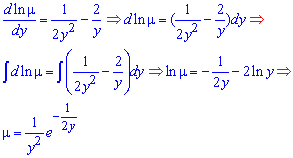
Після множення всіх членів рівняння на знайдений інтегруючий множник "м'ю" (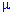
) отримаємо рівняння
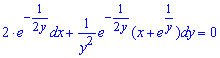
в повних диференціалах (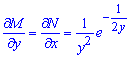
).
Далі будемо розв'язувати отримане рівняння, як у випадку повного диференціалу
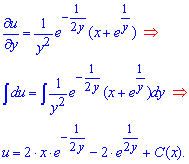
Запам'ятайте правило – якщо інтегрування іде по "ігрик", то константа залежить від "ікса", і навпаки.
Константу, що входить у рівняння до визначаютьо обчисленням часткової похідної знайденого розв'язок по "ікс" та при рівнянням до множника в диф. рівнянні при dx.
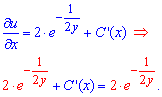
Звідси знаходимо сталу
Враховуючи все викладене вище, записуємо загальний інтеграл диференціального рівняння
В завданні необхідно знайти частковий розв'язок рівняння (задача Коші). Для цього записуємо додаткову умову на функцію
Звідси маємо частковий розв'язок диференціального рівняння
Він поки що записаний в неявній формі, проте в цьому випадку можемо знайти залежність функції від змінної y(x):
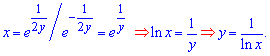- частковий розв'язок рівняння.
Приклад 2. (7.10) Знайти розв'язок задачі Коші:
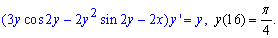Розв'язання: Записуємо задане диференціальне рівняння першого порядку через диференціали
Далі перевіримо чи маємо повний диференціал, виписуємо множники
,
та знаходимо часткові похідні
Умова на повний диференціал не виконується.
Перевіримо, чи не допускає це рівняння інтегруючого множника ?
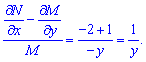
Отже, дане рівняння допускає інтегруючий множник, який залежить тільки від y. Знайдемо його інтегруванням рівняння
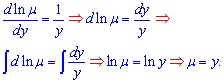
Після множення всіх членів рівняння на знайдений інтегруючий множник вихідне диф. рівняння перетвориться до вигляду
до рівняння в повних диференціалах
(
).
Як розв'язати таке рівняння Ви вже знаєте, тож переходимо до інтегрування простішого множника
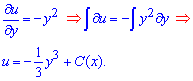
Щоб довизначити сталу – шукаємо часткову похідну функції u по "ікс" та прирівнюємо до другого множника в диф. рівнянні
Цього разу стала функція не рівна константі і для її встановлення потрібно знайти кілька інтегралів
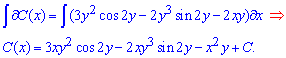
Загальний інтеграл диференціального рівняння при підстановці C(x)
має вигляд
Знайдемо частковий розв'язок рівняння (задача Коші):
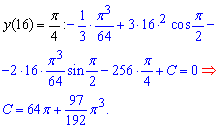
Звідси маємо
- частковий розв'язок диференціального рівняння.
Приклад 3. (7.21) Знайти розв'язок задачі Коші:
Розв'язання: Перепишемо рівняння розписавши похідну диференціалами
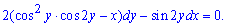
Далі діємо згідно методики для таких рівнянь.
Виписуємо множники біля диференціалів
Перевіряємо умову на повний диференціал функції
Умова на повний диференціал функції двох змінних не виконується.
Перевіримо, чи допускає рівняння інтегруючий множник?
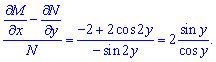
Як бачите, права сторона залежна від "ігрика", отже дане рівняння допускає інтегруючий множник.
Знайдемо його з рівняння
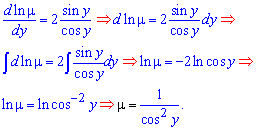
Після множення всіх членів рівняння на знайдений інтегруючий множник "м'ю" отримаємо таке рівняння в диференціалах
в повних диференціалах
(
).
Далі застосовуємо методику до диф. рівнянь в повних диференціалах. З першого доданку рівняння інтегруванням знаходимо залежність u(x)
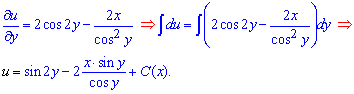
Далі обчислюємо часткову похідну функції u(x,y) по "ікс"
та порівнюємо з частковою похідною початкового рівняння
Неважко знайти звідси константу
Повертаємося та записуємо загальний інтеграл диференціального рівняння
За умовою потрібно знайти частковий інтеграл рівняння (розв'язати задачу Коші). Для цього обчислюємо значення функції в точці
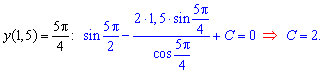
Константа рівна 2, а частковий розв'язок записуємо формулою
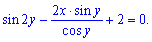
Для ясності відповіді знайдемо (обернену) залежність х(у):
- частковий розв'язок рівняння.
Красива відповідь незважаючи на масу перетворень та інтегрувань.
З наведених відповідей Ви маєте корисну інструкцію для обчислень. Для перевірки здобутих знань самоствйно знайдіть розв'язки рівнянь, використовуючи інтегруючий множник
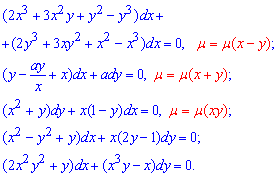Залишайтеся з нами, попереду ще багато готових прикадів з диференціальних рівнянь.
