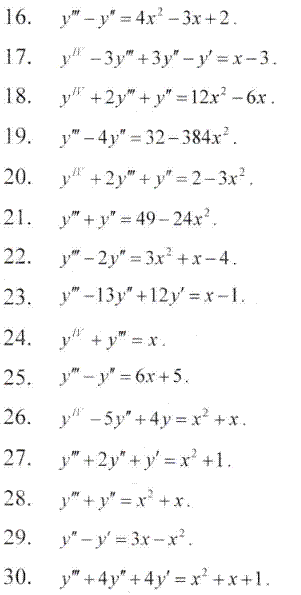З наведеної статі Ви отримаєте детальну інструкція для обчислення неоднорідного диференціального рівняння третього, четвертого порядку. Алгоритм знаходження загального розв'язку полягає у складанні характеристичного рівняння для однорідного ДР, а далі знаходженні часткового розв'язку неоднорідного ДР. В книжках все детально розписано, ми ж більше орієнтуємося на практичні заняття, тому переходимо до аналізу готових відповідей.
Приклад 1. (9.17) Знайти загальний розв'язок диференціального рівняння
![]()
Розв'язання: Маємо неоднорідне диференціальне рівняння четвертого порядку. Ви повинні знати, що розв'язок в таких рівняннях потрібно подати у вигляді суми інтегралу однорідного рівняння і часткового розв'язку неоднорідного ![]() .
.
Спершу завжди починаємо аналіз з однорідного диференціального рівняння
![]()
Подамо рішення у вигляд експоненти в степені y=ek*x.
Далі підставляємо у рівняння, і нехтуючи множником exp(k*x) (він завжди більший нуля), виписуємо характеристичне рівняння
![]() .
.
Розв'язавши його, отримаємо такі значення k1=0, k2=k3=k4=1.
Оскільки корені характеристичного рівняння є дійсні числа, причому три з них однакові, то розв'язок однорідного рівняння подамо у вигляді
![]()
Неоднорідна частина заданого рівняння x-3 має вигляд полінома P(x)ex, причому коефіцієнт у показниковій функції є коренем характеристичного рівняння (k=0, звідки e0*x=1), тому частковий розв'язок неоднорідного рівняння шукаємо у вигляді
![]()
Знайдемо коефіцієнти A і B: для цього підставимо функцію у вихідне диференціальне рівняння і прирівняємо множники при однакових степенях змінної x
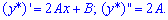
Третя і четверта похідні рівні нулю
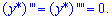
Підставляючи у рівняння і групуючи подібні вирази, отримаємо
![]()
звідки складаємо систему лінійних рівнянь
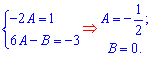
та знаходимо сталі A=-1/2 і B=0.
Отож, частковий розв'язок неоднорідного рівняння виражається формулою
![]()
Загальний розв'язок диференціального рівняння рівний сумі знайдених функцій
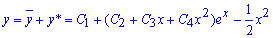
тут С1-С4 - довільні константи, які можна уточнити, якщо рівняння має умову Коші.
Приклад 2. (9.23) Знайти загальний розв'язок диференціального рівняння
![]()
Розв'язання: Розв'язок неоднорідного диференціального рівняння третього порядку за наведеною вище схемою подаємо через суму
![]() .
.
Спершу розглянемо однорідне диференціальне рівняння
![]()
Опускаючи проміжні дії, які описані в 1 завданні, записуємо характеристичне рівняння та знаходимо його корені
![]()
Так як корені характеристичного рівняння є різними, то розв'язок записуємо через суму експонент у різних степенях
![]()
Відповідно до правої частини рівняння (x-1) частковий розв'язок шукаємо у вигляді
![]()
Для визначення коефіцієнтів A, B обчислимо похідні першого – третього порядку
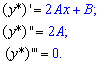
та підставимо у початкове диференціальне рівняння
![]()
Прирівнявши множники при однакових степенях змінної складаємо систему лінійних рівнянь
![]()
з якої знаходимо сталі
![]()
Можемо записати частковий розв'язок диференціального рівняння
![]()
Загальний розв'язок диференціального рівняння наступний
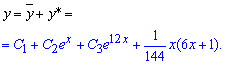
У ньому присутні три константи, які можуть приймати довільне значення. Довизначити їх може лише умова Коші, проте в завданні вона не задана.
Приклад 3.(9.12) Розв'язок диференціальне рівняння
![]()
Розв'язання: Завдання подібне до першого. Розв'язок неоднорідного диференціального рівняння четвертого порядку шукаємо через суму двох.
1. Для однорідного диференціального рівняння
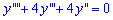
характеристичне рівняння після підстановки функції y=exp(k*x) матиме вигляд
![]()
Корені шукати в більшості випадків легко, для прикладу дане має розв'язком нуль кратності 2, інші два корені знаходимо з квадратного рівняння
k2-4k+4=0
за теоремою Вієта. В результаті отримаємо k1=k2=0 та k3=k4=-2. Оскільки корені характеристичного рівняння є дійсні числа, причому кожні 2 з них однакові (кратні), то розв'язок однорідного диференціального рівняння записуємо у вигляді
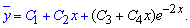
Неоднорідна частина заданого рівняння x-x2 має вигляд поліному другого порядку P2(x), тому частковий розв'язок шукаємо у вигляді
![]()
Знайдемо коефіцієнти A, B і D : для цього функцію підставляємо у початкове диференціальне рівняння і прирівняємо коефіцієнти при однакових степенях x:
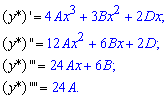
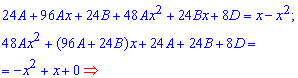
В результаті прийдемо до систему з 3 лінійних рівнянь
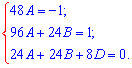
Мудрувати тут не приходиться – маємо готову схему Гауса, тому послідовно з першого рівняння знаходимо A , з другого B, третього – D
![]()
Підставляємо знайдені величини у формулу часткового розв'язку рівняння
![]()
Загальний розв'язок диференціального рівняння 4 порядку знаходимо сумуванням функцій:
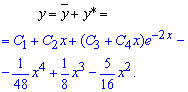
Сталі С1, С2, С3, С4 – приймають довільні значення. Якщо завдання містить задачу Коші то сталі визначають з початкової умови.
На цьому ознайомлення з методикою обчислень диференціальних рівнянь через характеристичне рівняння завершено. Вдосконалюйте вміння диференціювати та інтегрувати і з часом подібні ДР для Вас будуть легкими.
А для цього потрібно багато працювати самостійно, тому як домашнє завдання спробуйте знайти розв'язки наступних диференціальних рівнянь.