Неоднорідне диференціальне рівняння за складністю обчислень можна розділити на два типи: перший має неоднорідну функцію, яка не пов'язана з розв'язком однорідного рівняння. Другий тип передбачає, що неоднорідна частина ДР може містити експоненту, синуси та косинуси або добутки експонент на синуси та косинуси. Легший з варіантів ДР детально розглянуто на попередніх уроках. Далі будуть проаналізовані готові відповіді на складні неоднорідні ДР 3 порядку: в цій статті завдання, що містять експоненту, у наступних - тригонометричні функції.
Зразу хочу звернути Вашу увагу, що на важливих моментах при обчисленнях наголошено і їх слід завчити, чи виписати. Загалом матеріал повинен Вам сподобатися та допомогти в навчанні!
Як розв'язати неоднорідне диференціальне рівняння?
Приклад 1. (10.16) Знайти загальний розв'язок диференціального рівняння:
Розв'язання. Маємо неоднорідне диференціальне рівняння третього порядку, одне із складних в даному розділі. Його розв'язок шукаємо через суму розв'язків однорідного та неоднорідно диф. рівнянь 
. Знайдемо кожен із коренів, для цього виконуємо аналіз однорідного диференціального рівняння
Його розв'язок шукаємо у вигляді суми експоненціальних функцій
y=exp(k*x).
При підстановці в однорідне рівняння, та діленні на exp(k*x) (завжди більше нуля) отримаємо характеристичне рівняння
Оскільки рівняння кубічне, то один з коренів шукаємо серед простих множників вільного члена інші два – з неповного квадратного рівняння, що залишиться
(k2-1)(k-3)=0.
У результаті отримаємо наступні значення
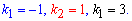
Так як корені характеристичного рівняння є різними дійсними числами, то розв'язок має вигляд суми добутку констант на експоненти у відповідних степенях
Права частина диференціального рівняння (4-8x)ex має вигляд полінома помноженого на степеневу залежність експоненти P(x)ex, причому коефіцієнт в показниковій функції є коренем характеристичного рівняння (k=1), тому частковий розв'язок запишемо у вигляді
А і В, що входять в формулу функції. Для цього підставимо y в диференціальне рівняння і прирівняємо коефіцієнти при однакових степенях x. Обчислюємо похідні до третього порядку
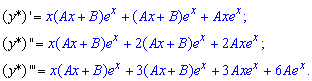
та підставляємо у початкове диференціальне рівняння. Після об'єднання подібних доданків отримаємо залежність
Звідси при однакових степенях змінної визначаємо сталі A=1, B=-1.
Таким чином, частковий розв'язок ДР можемо записати формулою
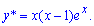
Загальний розв'язок диференціального рівняння знаходимо сумуванням функцій
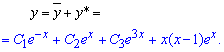
Тут С1, С2, С3 – сталі, що приймають довільні значення. Довизначити їх можемо лише за наявності умови Коші для розв'язку.
Тепер Ви знаєте, як розв'язати неоднорідне диференціальне рівняння такого виду.
Приклад 2. (10.22) Знайти загальний розв'язок диференціального рівняння
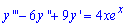
Розв'язання: Розв'яжемо неоднорідне диференціальне рівняння третього порядку через суперпозицію двох коренів .
Опускаючи викладки, які можете прочитати з попереднього завдання, запишемо характеристичне рівняння для однорідного диф. рівняння і знайдемо його корені
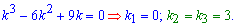
Оскільки два корені є однаковими, то загальний інтеграл однорідного ДР має вигляд
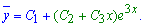
Права частина заданого рівняння 4x*ex 
має вигляд полінома першого степеня P(x) помноженого на експоненціальну функцію exp(x), тому і частковий розв'язок рівняння шукаємо у такому ж вигляді
Знаходимо похідні до третього порядку
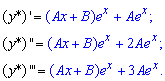
та підставляємо у початкове ДР. Після об'єднання подібних доданків отримаємо
Звідси знаходимо сталі – А=1; В=0. Можемо записати явний вигляд часткового розв'язку ДР 
Загальний інтеграл диференціального рівняння знаходимо, як суму знайдених функцій
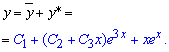
На цьому завдання розв'язане.
Приклад 3.(10.24) Знайти загальний розв'язок диференціального рівняння:
Розв'язання: Корені неоднорідного диференціальне рівняння третього порядку за відомою Вам схемою шукаємо у вигляді суми
Для однорідного диференціального рівняння характеристичне рівняння має вигляд
Розв'язавши його, отримаємо три корені, причому один кратності 2
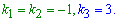
У таких випадках відповідь записуємо формулою
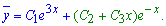
Права частина неоднорідного диф. рівняння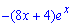 
має вигляд P(x)ex, при цьому степінь експоненти не співпадає з характеристичними коренями, тому в аналогічному вигляді шукаємо частковий розв'язок
Знаходимо похідні до третього порядку
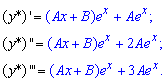
Підставляємо їх у диференціальне рівняння і групуємо спільні доданки, в результаті матимемо
звідки, прирівнявши коефіцієнти при однакових степенях аргументу визначаємо сталі A=1; B=0.
Отож, частковий розв'язок рівняння можемо записати залежністю
Далі сумуванням знаходимо загальний розв'язок диференціального рівняння
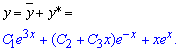
Як можна переконатися з наведених завдань, обчислення не надто складні. Якщо маєте завдання, які важко самостійно вирішити - просьба надсилати їх нам на пошту. Ми постійно шукаємо та підбираємо завдання, які навчать Вас нового та в повній мірі розкриють тему.
Під час навчання Вам приходилося брати куди важчі похідні та інтеграли, схема розв'язування неоднорідних рівнянь теж не складна і під силу запам'ятати кожному.
Щоб матеріал Вам краще засвоївся, знайдіть у методичках за якими вчитеся схожі диференціальні рівняння та розв'яжіть самостійно. Повірте - це набагато більше Вам допоможе, ніж прочитати на сайті і сказати -"Я все зрозумів!". Щоб потім не було на модулі чи контрольній питань "Як розв'язати неоднорідне диференціальне рівняння?"
І знайте - у разі труднощів ми готові Вам допомогти.
