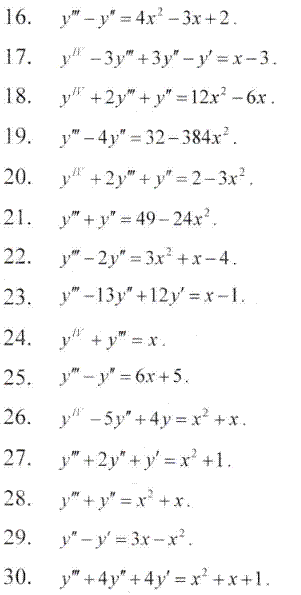Из приведенной статьи Вы получите подробную инструкция для вычисления неоднородного дифференциального уравнения третьего, четвертого порядка. Алгоритм нахождения общего решения заключается в составлении характеристического уравнения для однородного ДУ а потом нахождении частного решения неоднородного ДУ. В книгах все подробно расписано, мы же больше ориентируемся на практические занятия, поэтому переходим к анализу готовых ответов.
Пример 1. (9.17) Решить дифференциальное уравнение
![]()
Решение: Имеем неоднородное дифференциальное уравнение четвертого порядка. Вы должны знать что решение в таких уравнениях нужно представить в виде суммы интеграла однородного уравнения и частного решения неоднородного ![]() .
.
Сначала всегда начинаем анализ с однородного дифференциального уравнения
![]()
Представим решение в вид экспоненты в степени y=ek*x.
Далее подставляем y в уравнение и, пренебрегая множителем exp(k*x) (он всегда больше нуля), выписываем характеристическое уравнение
![]()
Решив его получим следующие значения k1=0, k2=k3=k4=1.
Поскольку корни характеристического уравнения действительны числа, причем три из них одинаковые, то решение однородного уравнения представим в виде
![]()
Неоднородная часть заданного уравнения x-3 имеет вид полинома P(x)ex, причем коэффициент в показательной функции является корнем характеристического уравнения (k=0, откуда e0*x=1), поэтому частичный решение неоднородного уравнения ищем в виде
![]()
Найдем коэффициенты A и B: для этого подставим функцию в исходное дифференциальное уравнение и приравняем множители при одинаковых степенях переменной x
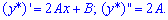
Третья и четвертая производные равны нулю
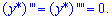
Подставляя в уравнение и группируя подобные выражения, получим
![]()
откуда составляем систему линейных уравнений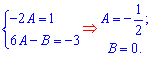
и находим сталые A=-1/2 и B=0.
Таким образом частичное решение неоднородного уравнения выражается формулой
![]()
Общее решение дифференциального уравнения равно сумме найденных функций
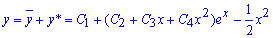
здесь С1-С4 - произвольные константы, которые можно уточнить если уравнение имеет условие Коши.
Пример 2. (9.23) Найти интеграл дифференциального уравнения![]()
Решение: Решение неоднородного дифференциального уравнения третьего порядка по приведенной выше схеме подаем через сумму
![]()
Сначала рассмотрим однородное дифференциальное уравнение![]()
Опуская промежуточные действия, которые описаны в 1 задании, записываем характеристическое уравнение и находим его корни
![]()
Так как корни характеристического уравнения различные, то решение записываем через сумму экспонент в соответственных степенях ![]()
Согласно правой части уравнения (x-1) частичное решение ищем в виде
![]()
Для определения коэффициентов A, B вычислим производные первого - третьего порядка 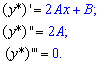
и подставим в исходное дифференциальное уравнение
![]()
Приравняв множители при одинаковых степенях переменной составляем систему линейных уравнений
![]()
из которой находим постоянные![]()
Теперь можем записать частичное решение дифференциального уравнения![]()
Общее решение дифференциального уравнения находим по формуле
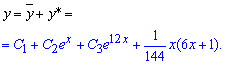
В нем присутствуют три константы, которые могут принимать произвольное значение. Доопределить их может только условие Коши, однако в задании оно не задано.
Пример 3.(9.12) Решить дифференциальное уравнение
![]()
Решение: Решение неоднородного дифференциального уравнения четвертого порядка ищем через сумму двух.
1. Для однородного дифференциального уравнения
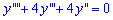
характеристическое уравнение после подстановки функции y=exp(k*x) будет иметь вид
![]()
Корни искать в большинстве случаев легко, например данное имеет решением ноль кратности 2, остальные два корня находим по теореме Виета с квадратного уравнения
k2-4k+4=0
В результате получим k1=k2=0 и k3=k4=-2. Поскольку корни характеристического уравнения действительны числа, причем каждые 2 из них одинаковые (кратные), то решение однородного дифференциального уравнения записываем в виде 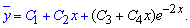
Неоднородная часть заданного уравнения x-x2 имеет вид полинома второго порядка P2(x), поэтому частичный решение ищем в виде
![]()
Найдем коэффициенты A, B и D : для этого функцию подставляем в исходное дифференциальное уравнение и приравниваем коэффициенты при одинаковых степенях x:
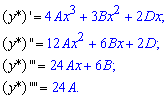
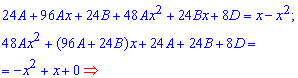
В результате придем к системе из 3 линейных уравнений
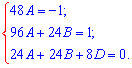
Мудрить здесь не приходится - имеем готовую схему Гаусса, поэтому последовательно с первого уравнения находим A, с второго - B, третьего - D
![]()
Подставляем найденные значения в формулу частного решения уравнения![]()
Общее решение дифференциального уравнения 4 порядка находим суммированием функций
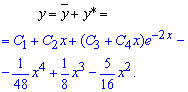
Сталые С1, С2, С3, С4 – принимают произвольные значения. Если задание содержит задачу Коши то их определяем с начального условия.
На этом знакомство с методикой вычисления дифференциальных уравнений через характеристическое уравнение завершено. Совершенствуйте умение дифференцировать и интегрировать и со временем подобные Ду для Вас также будут легкими.
А для этого нужно много работать самостоятельно, поэтому в качестве домашнего задания попробуйте найти решение следующих дифференциальных уравнений.