Серед прикладів рівнянь з модулями часто зустрічаються рівняння де потрібно знайти корені рівняння вигляду "модуль в модулі" (вкладені модулі), тобто рівнянь виду
||a*x-b|-c|=k*x+m.
Якщо k=0, тобто права сторона рівна сталій (m) то знайти розв'язок рівняння з модулями можна швидше графічним методом. Нижче наведена методика розкриття подвійних модулів на поширених для практики прикладах. Добре розберіть алгоритм обчислення рівнянь з модулями, щоб не мати труднощів на контрольних, тестах, та просто, щоб знати як їх розкривати.
Приклад 1. Розв'язати рівняння виду модуль в модулі |3|x|-5|=-2x-2.
Розв'язання: Завжди починають розкривати рівняння з внутрішнього модуля
|x|=0 <-> x=0.
В точці x=0 рівняння розділяється на 2.
При x<0 підмодульна функція від'ємна, тому при розкритті знак змінюємо на протилежний
|-3x-5|=-2x-2.
При x>0 або рівне 0, розкриваючи модуль отримаємо
|3x-5|=-2x-2.
Розв'яжемо рівняння для від'ємних змінних (x<0). Воно розкладається на дві системи рівнянь.
Перше р-ня системи отримуємо з умови, що функція за знаком рівності невід'ємна.
Друге – розкриваючи модуль в одній системі приймаємо, що підмодульна функція додатна, в іншій від'ємна – змінюємо знак правої або лівої частини
(залежить від методики викладання).
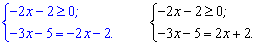
З першого рівняння отримаємо, що невідома не повинна перевищувати (-1), тобто
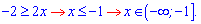
Це обмеження повністю належить області, в якій розв'язуємо.
Перенесемо змінні і сталі по різні сторони рівності в першій і другій системі
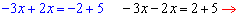
та знайдемо разв'язки
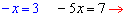
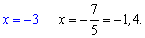
Обидва значення належать проміжку, що розглядається, тобто є коренями.
Розглянемо рівняння з модулем при додатних змінних
|3x-5|=-2x-2.
Опускаючи модуль, матимемо дві системи рівнянь
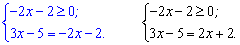
З першого рівняння, яке є спільним для двох сиcтем, отримаємо знайому умову
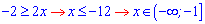
яка в перетині з множиною, на якій шукаємо розв'язок дає порожню множину
(немає точок перетину).
Звідси випливає, що єдиними коренями модуля з модулем є значення
x=-3; x=-1,4.
Приклад 2. Розв'язати рівняння ||x-1|-2|=3x-4.
Розв'язання: Почнемо з розкриття вложеного модуля
|x-1|=0 <=> x=1.
Підмодульна функція змінює знак в одиниці. При менших значеннях вона від'ємна, при більших – додатна. Відповідно до цього при розкритті вкладеного модуля отримаємо два рівняння з модулем
x |-(x-1)-2|=3x-4;
x>=1 -> |x-1-2|=3x-4.
Обов'язково перевіряємо праву сторону рівняння з модулем, вона завжди повинна бути невід'ємною.
(модуль від'ємним не буває)
3x-4>=0 -> x>=4/3.
Це означає, що перше з рівнянь немає необхідноcті розв'язувати, оcкільки його випиcано для x< 1, що не відповідає знайденій умові.
Розкриємо модуль в другому рівнянні
|x-3|=3x-4 ->
x-3=3x-4 або x-3=4-3x;
4-3=3x-x або x+3x=4+3;
2x=1 або 4x=7;
x=1/2 або x=7/4.
Отримали два значення, перше з яких відкидаємо, оскільки не належить розглядуваному інтервалу. Остаточно, рівняння має один розв'язок x=7/4.
Приклад 3. Знайти корені рівняння ||2x-5|-1|=x+3.
Розв'язання: Розкриємо внутрішній модуль
|2x-5|=0 <=> x=5/2=2,5.
Точка x=2,5 розбиває числову вісь на два інтервали. Відповідно, підмодульна функція змінює знак при переході через точку 2,5.
Випишемо умову на розв'язок (ОДЗ) з правої сторони рівняння з модулем.
x+3≥0 -> x≥-3.
Тому розв'язком можуть бути значення, які не менші за (-3).
Розкриємо модуль для від'ємного значення внутрішнього модуля
|-(2x-5)-1|=x+3;
|-2x+4|=x+3.
Цей модуль теж при розкритті дасть 2 рівняння
-2x+4=x+3 або 2x-4=x+3;
2x+x=4-3 або 2x-x=3+4;
3x=1; x=1/3 або x=7.
Значення x=7 відкидаємо, оскільки ми шукали розв'язок на проміжку [-3;2,5].
Далі розкриваємо внутрішній модуль для x>2,5.
Дістанемо рівняння
|2x-5-1|=x+3;
|2x-6|=x+3.
При розкритті модульне рівняння розділяється на два лінійні
-2x+6=x+3 або 2x-6=x+3;
2x+x=6-3 або 2x-x=3+6;
3x=3; x=1 або x=9.
Перше значення x=1 не задовольняє умову x>2,5. Тому на цьому інтервалі маємо один корінь рівняння з модулем x=9, а всього їх два (x=1/3). Підстановкою можна перевіряти правильність виконаних обчислень.
Відповідь: x=1/3; x=9.
Приклад 4. Знайти розв'язки рівняння ||3x-1|-5|=2x-3.
Розв'язання: Розкриємо вкладений модуль
|3x-1|=0 <=> x=1/3.
Точка x=2,5 ділить дійсну вісь на два інтервали, а задане рівняння на два випадки.
Записуємо умову на розв'язок, виходячи з того, що права сторона повинна бути невід'ємною
2x-3>=0 -> x≥3/2=1,5.
Звіди слідує, що нас цікавлять значення, які ≥1,5. Таким чином, модульне рівняння розглядаємо на двох інтервалах
[1,5; 2,5], [2,5; +безмежність).
Розкриємо модуль при від'ємних значеннях вкладеного модуля [1,5; 2,5]
|-(3x-1)-5|=2x-3;
|-3x-4|=2x-3.
Отриманий модуль при розкритті розділяється на 2 рівняння
-3x-4=2x-3 або 3x+4=2x-3;
2x+3x=-4+3 або 3x-2x=-3-4;
5x=-1; x=-1/5 або x=-7.
Обидва значення не належать проміжку [1,5; 2,5], тому не є розв'язками рівняння з модулями.
Далі розкриємо внутрішній модуль для x>2,5. Отримаємо:
|3x-1-5|=2x-3;
|3x-6|=2x-3.
Розкриваючи модуль, отримаємо:
3x-6=2x-3 або –(3x-6)=2x-3;
3x-2x=-3+6 або 2x+3x=6+3;
x=3 або 5x=9; x=9/5=1,8.
Друге значення із знайдених розв'язків не відповідає умові x>2,5, тому його відкидаємо.
Оcтаточно дістанемо один корінь рівняння з модулями x=3.
Виконуємо перевірку
||3*3-1|-5|=2*3-3 3=3.
Підстановка показує, що корінь рівняння з модулем обчислено вірно.
Відповідь: x=1/3; x=9.
Прикладів з модулями, де маємо один або декілька вкладених модулів в інтернеті, чи методичках можна знайти чимало. Схема їх обчислень нічим не відрізняється від наведеної вище. Для перевірки знань прошу розв'язати наступні завдання.
Рівняння типу на модуль в модулі:
- ||3x-3|-2|=5-2x;
- ||5x-3|-3|=3x-1;
- ||2x-7|-4|=x-2;
- ||5x-4|-8|=x+4;
- ||2x-2|-3|=1;
- ||x-2|-3|=4-x.
Переглянути схожі матеріали:


