Поширеними прикладами з модулями є рівняння типу модуль в модулі. Подвійний модуль можна записати у вигляді формули
||a*x-b|-c|=k*x+m.
Якщо k=0 то таке рівняння з модулем легше розв'язувати графічним методом. Класичне розкриття модулів в таких ситуаціях громіздке і не дає бажаного ефекту на контрольних та тестах. Графічний метод дозволяє за швидкий час виконати побудову модульних функцій і знайти кількість коренів рівняння.
Алгоритм побудови подвійного, потрійного модуля досить простий і з наведених нижче прикладів сподобається багатьом. Для закріплення методики внизу наведені приклади для самостійного обчислення.
Приклад 1. Розв'язати рівняння модуль в модулі ||x-3|-5|=3.
Розв'язання: Розв'яжемо рівняння з модулями класичним методом та графічно. Знайдемо нуль внутрішнього модуля
x-3=0 x=3.
В точці x=3 рівняння з модулем розділяється на 2. Крім цього, нуль внутрішнього модуля є точкою симетрії графіка модулів і якщо права сторона рівняння рівна сталій, то корені лежать на однаковій відстані від цієї точки. Тобто можна розв'язати одне рівняння з двох, а решту коренів обчислити з цієї умови.
Розкриємо внутрішній модуль для x>3
|x-3-5|=3; |x-8|=3.
Отримане рівняння при розкритті модуля ділиться на 2
Підмодульна функція >0
x-8=3; x=3+8=11;
і для х< 0 матимемо
-(x-8)=3; x=8-3=5.
Обидва корені рівняння задовольняють умову x>3, тобто є розв'язками.
Враховуючи записане вище правило симетрії розв'язків рівняння з модулями, можна не шукати корені рівняння для x< 3, яке має вигляд
|-(x-3)-5|=3; |-x-2|=3,
а обчислити їх.
Значення симетричне відносно x=3 для x=11 рівне
x=3-(11-3)=6-11=-5.
За тією ж формулою знаходимо другий розв'язок
x=3-(5-3)=6-5=1.
Задане рівняння модуля в модулі має 4 розв'язки
x=-5; x=1; x=5; x=11.
Тепер знайдемо розв'язки рівняння з модулями графічним методом. З внутрішнього модуля |x-3| слідує, що графік стандартної модуль функції є зміщений по осі Ох вправо на 3.
Дальше відняти 5 означає, що графік необхідно опустити на 5 по осі Oy. Щоб отримати модуль отриманої функції симетрично відображаємо все, що знаходиться нижче осі Ox.
І наостанку виконуємо побудову прямої y=3, яка паралельна осі Ox. Найкраще для обчислень рівнянь з модулями графічно використовувати зошит в клітинку, оскільки в ньому зручно будувати графіки.
Остаточний вигляд графіка модулів має вигляд
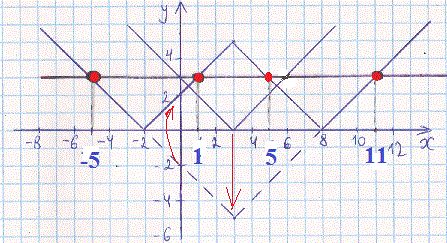
Точки перетину модуль функції і прямої y=3 і є шуканими розв'язками.
Перевага графічного методу над розкриттям модулів для простіших рівнянь очевидна. Однак графічно незручно шукати корені коли права сторона має вигляд k*x+m, тобто пряму нахилену до осі абсцис під кутом.
Тут таких рівнянь розглядати не будемо.
Приклад 2. Скільки коренів має рівняння ||2x-3|-2|=2?
Розв'язання: Права сторона рівна сталій, тому швидше знайти розв'язок можна графічним методом. Внутрішній модуль перетворюється в нуль
|2x-3|=0 x=3/2=1,5
в точці x=1,5.
Значить в цю точку зміщуємо графік функції y=|2x|. Для того, щоб його побудувати підставте декілька точок та проведіть через них прямі. Від отриманої функції віднімаємо 2, тобто графік опускаємо на двійку вниз і, щоб отримати модуль переносимо від'ємні значення (y< 0) симетрично відносно осі Ox.
Далі залишається побудувати праву сторону (пряму y=2) та підрахувати кількість точок перетину. Графік модуль функції та прямої зображено нижче
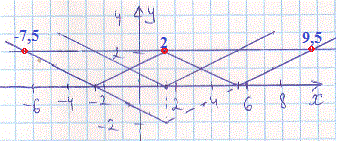
Бачимо, що задане рівняння має три розв'язки.
Приклад 3. При якому значенні параметра a рівняння з модулем |||x+1|-2|-5|=a має 5 розв'язків?
Розв'язання: Маємо рівняння з трьома вкладеними модулями. Знайдемо відповідь з графічного аналізу. Почнемо, як завжди, з внутрішнього модуля. Він перетворюється в нуль
|x+1|=0 x=-1
в точці x=-1.
Будуємо графік модуль функції в цій точці.
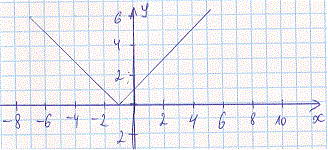
Далі графік опускаємо вниз на двійку і від'ємні значення (y< 0) симетрично переносимо вгору. Отримаємо графік функції
y=||x+1|-2|
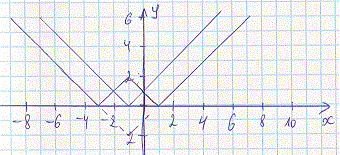
Повторно виконаємо зміщення графіку модуль функції вниз на 5 і симетричне перенесення від'ємних значень функції. В результаті отримаємо ліву сторону рівняння з модулями
y=|||x+1|-2|-5|.
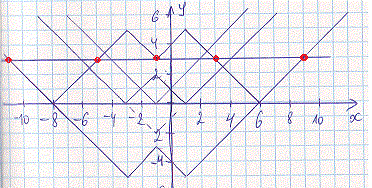
Параметр а відповідає значенню паралельної прямої, яка повинна перетнути графік модуль функції в 5 точках. Спочатку проводимо таку пряму, далі шукаємо точку перетину її з віссю Oy.
Це пряма y=3, тобто шуканий параметр рівний a=3.
Методом розкриття модулів дане завдання можна було розв'язувати цілий урок, якщо не більше. Тут все звелося до кількох графіків.
Відповідь: a=3.
Приклад 4. Скільки розв'язків має рівняння |||3x-3|-2|-7|=x+5 ?
Розв'язання: Розкриємо внутрішній модуль рівняння
|3x-3|=0 <=> x=3/3=1.
Будуємо графік функції y=|3x-3|. Для цього на одну клітинки зміни x від знайденої точки додаємо 3 клітинки по y. Виконуйте побудову коренів рівняння в зошиті в клітинку, а я розкажу як це можна зробити в середовищі Maple.
restart;with(plots): Занулюємо всі змінні і підключаємо модуль для роботи з графікою.
Далі будуємо графік внутрішнього модуля. Значення x=-2..4 вказують в яких межах змінної виконати побудову.
> plot(abs(3*x-3),x=-2..4):
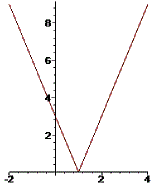
Далі опускаємо графік на 2 клітинки донизу і симетрично осі Ox переносимо від'ємні значення (y< 0).
Отримаємо графік двох внутрішніх модулів Отриманий графік опускаємо на двійку і симетрично відображаємо. Отримаємо графік
y=||3x-3|-2|.
В математичному пакеті це рівносильне запису ще одного модуля
> plot(abs(abs(3*x-3)-2),x=-2..4):
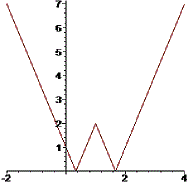
Повторно зміщуємо графік донизу на сім одиниць і симетрично переносимо. Отримаємо графік функції
y=|||3x-3|-2|-7|
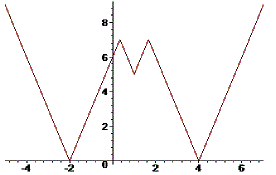
В Мейплі це рівносильно наступній стрічці коду
> plot(abs(abs(abs(3*x-3)-2)-7),x=-5..7):
Будуємо пряму y=x+5 за двома точками. Перша – перетин прямої з віссю абсцис
у=0: x+5=0;x=-5 (-5;0)
Друга – осі ординат
х=0: y=0+5=5 (0;5).
Через знайдені точки проводимо пряму.
В Мейплі використаємо функції відображення кількох графіків display.
Для цього дамо назву графіку модуль функції.
> q1:=plot(abs(abs(abs(3*x-3)-2)-7),x=-5..9):
Далі виконаємо побудову правої частини рівняння – прямої y=x+5.
> q2:=plot(x+5,x=-5..10,color=blue):
властивість color відповідає за колір кривих на графіку, ще Вам деколи може знадобитись thickness=2; 3 – це товщина ліній.
Вкінці рядка варто ставити знак ":" а не ";", що не виводило зайвого коду.
Ну і вкінці відображаємо два графіки
> display(q1,q2);
Результатом буде наступний рисунок.
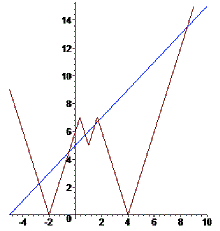
Звідси бачимо, що модуль з прямою має 6 точок перетину, отже є 6 розв'язків рівняння.
Рівняння на модуль в модулі:
- |||2x-3|-4|-7|=3;
- |||x+2|-3|-1|=1;
- |||x+3|-1|-4|=3;
- ||2x+3|-5|=3;
- ||5x-4|-4|=3;
- ||x-7|-2|=1.
Переглянути схожі матеріали:


