Під простими рівняння з модулями маємо на увазі рівняння виду
|x|=5; |x-3|=2; ||2x-1|-5|=3; |1-x|=4
в яких змінна входить одноразово та лінійно.
Розв'язувати модульні рівняння можна як за допомогою розкриття модулів так і графічно. В даній статті більша увага буде приділена саме графічному методу розкриття модулів. Для цього поступово буде розкрита суть перетворень з модулями. В такий спосіб вдається розв'язати безліч тестових задач, в яких потрібно знайти кількість розв'язків рівняння з модулем.
Для наочності наведемо графік функції y=|x|
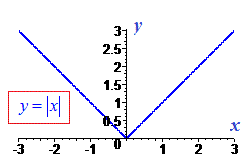
Далі зобразимо зміщення графіку модуль функції по осі Ox, наприклад y=|x-7|. Такий запис означає, що функція рівна нулю, коли дужа рівна нулю
x-7=0; –> x=7.
Отже "галочка" переноситься вправо на 7.
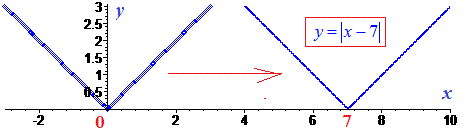
Якщо підмодульну функцію помножити на (-1) то графік функції не зміниться |7-x|=|x-7|.
Якщо під модулем маємо додавання |x+5|, то зміщення графіка модуль функції виконуємо в бік від'ємних змінних
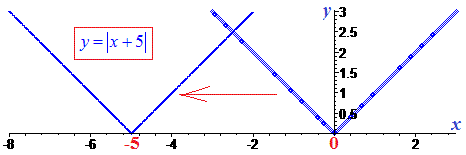
Самі цікаве в обчисленнях відбувається коли маємо рівняння виду модуль в модулі
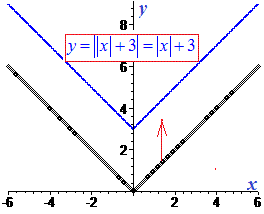
||x|-6|, ||x|+3|
Тоді виконуємо перенесення графіку внутрішнього модуля по осі вниз або вгору, та симетричне відображення значень, які йдуть нижче осі Oх угору.
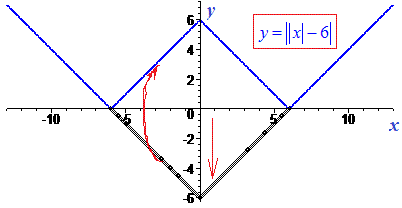
Друга функція, це модуль піднятий угору на три.
Далі, якщо в завданні питають "Яка кількість коренів рівняння ||x|-6|=2?" , то необхідно провести лиш лінію y=2 і підрахувати кількість точок перетину з графіком модуля
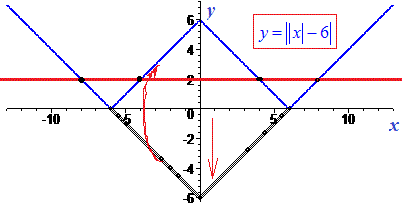
Рівняння має 4 розв'язки. Найкраще розв'язувати графічно рівняння з модулями на листку в клітинку, є краща прив'язка до квадратиків. Завдання в кожному з випадків зводиться до зміщення, відображення та паралельного переносу графіка модуль функції |x|.
Приклад 1. Знайти корені рівняння ||x-2|-5|=3.
Розв'язання: Маємо завдання типу модуль від модуля. Виконуємо побудову першого (внутрішнього) модуля
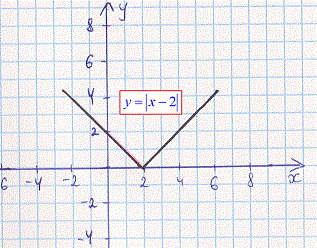
Далі паралельно переносимо лінії вниз на 5, щоб отримати графік y=|x-2|-5
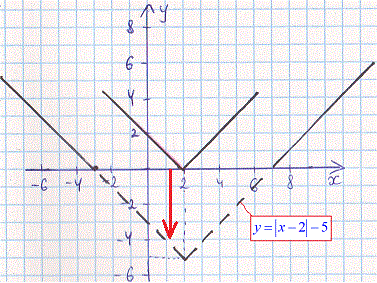
Наступним кроком віддзеркалюємо все, що знаходиться нижче осі абсцис. Це і буде шукана модуль функція y=||x-2|-5|. Також виконуємо побудову прямої у=3
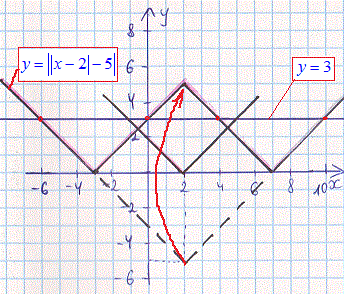
Неважко визначити з рисунку, що розв'язками рівняння з модулями будуть
x=-6; x=0;x=4; x=10.
На цьому приклад розв'язано. Далі буде менше деталізації, проте суть алгоритму Вам буде зрозуміла.
Приклад 2. Знайти кількість коренів наступного рівняння з модулем
|||x+1|-3|-5|=2.
Розв'язання: Задано рівняння з двома вкладеними модулями. Графік першого вкладеного модуля отримаємо зміщенням в від'ємний бік осі абсцис модуль функції на одиницю. Далі паралельно переносимо отриманий графік вниз на 3 та відобразимо відносно осі Ox всі мінусові y. Отриманий графік знову опускаємо вниз, цього разу на 5 та симетрично відображаємо все, що знаходиться нижче осі Ox. Виконуємо побудову правої сторони рівняння – y=2.
В результаті у Вас повинен вийти схожий кінцевий графік модуль функції
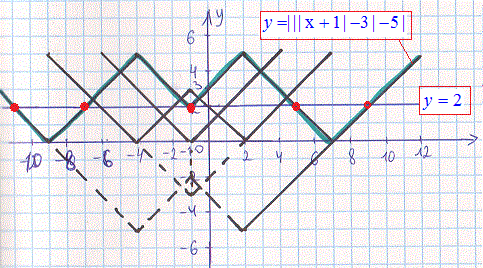
Бачимо, що маємо п'ять точок перетину прямої з модуль-функцією, а отже і 5 коренів рівняння.
Приклад 3. При якому значенні параметра a рівняння з модулем ||x-4|-2|=a-3 має три, чотири корені?
Розв'язання: Виконуємо побудову заданих модулів, що є в лівій частині рівняння з модулями
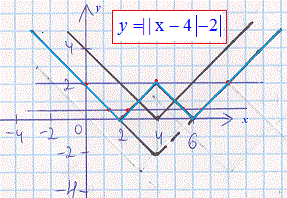
З побудови бачимо, якщо права сторона рівняння з модулями рівна 2, то маємо три корені. Якщо від 0 до 2, не включаючи країв – маємо 4 корені рівняння. Звідси отримаємо рівняння для знаходження параметра
a-3=2; – > a=5.
та нерівності
a-3>0; a>3;
a-3< 2; a < 5 .
Підсумовуємо: рівняння має 3 корені коли параметр рівний a=5
і 4 корені, якщо параметр належить інтервалу a=(3..5).
В подібних прикладах треба бути дуже уважними, оскільки часто саме запитання ставиться так, щоб допомогти Вам або навпаки. Наприклад: "Скільки додатних коренів має рівняння з модулями?", "Знайдіть суму розв'язків рівняння", "Знайдіть найбільше ціле значення параметра" і тому подібні. Тому вдумливо читайте, що від Вас вимагають, а вже тоді приступайте до обчислень.
Переглянути схожі матеріали:


