Ірраціональні рівняння взяті із із "Збірника задач для вступників. Математика" виданого Волинським державним університетом імені Лесі Українки у 2001 році. Їх розв'язування має практичний інтерес для школярів, абітурієнтів, викладачів. Тож не гайте часу та вивчіть методи обчислень ірраціональних рівнянь.
Приклад 1. Визначити менший корінь ірраціонального рівняння
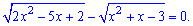
Розв'язання. Схема обчислень такого сорту прикладів наступна:
Переносимо від'ємний доданок за знак рівності і підносимо корені до квадрату. Щоб не виникла ситуація, коли під коренем отримаємо від'ємне значення в кінці обов'язково перевіряємо відповідь
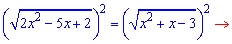
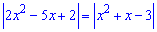
Оскільки підкореневий вираз повинен бути додатній, то модулі опускаємо і групуємо подібні доданки
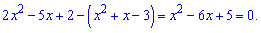
Отримане квадратне рівняння за теоремою Вієта має корені x=1; x=5. В умові питають за менший корінь, і тут половина із Вас у відповідь впише x=1. І це буде неправильно! Спробуйте підставити одиницю в рівняння
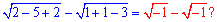
Отримали корені з від'ємних чисел. Це в ірраціональних рівняннях недопустимо, в комплексних числах звична ситуація, але в 10 класі комплексні числа не вчать. Тепер спробуйте підставити x=5
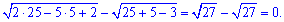
Отримали тотожність і перевірили єдиний правильний розв'язок ірраціонального рівняння (x=5). Він і є найменшими для заданого прикладу. Взагалі кажучи, тестові завдання при вступі так і побудовані, що Ви довго розв'язуєте, тратите дорогоцінний час. І якщо не перевірите правильність розв'язку, то можете недорахуватися декількох потрібних для вступу балів. Тому будьте уважні при вирішенні ірраціональних прикладів на тестах, контрольних, зрізах.
Приклад 2. Визначити більший корінь рівняння
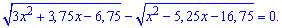
Розв'язання. Схему для такого завдання Ви вже знаєте. Записуємо область допустимих значень коренів
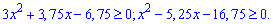
Зводимо ірраціональне рівняння до квадратного
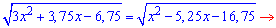
Підносимо до квадрату та згрупуємо подібні доданки
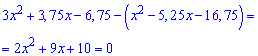
Обчислю дискримінант рівняння
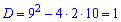
та корені рівняння
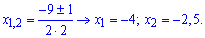
І знову заковирка – хто не знає від'ємних чисел тягнеться поставити у відповідь x=-4. Однак -2,5 є більше за -5. Хто відповість x=-2,5 теж може виявитися неправим, якщо виявиться, що значення не задовольняє ОДЗ. Тому для себе зробіть простий висновок – після обчислення ірраціональних рівнянь перевіряйте розв'язки підстановкою. Оскільки -2,5>-5, то ми його і перевіримо
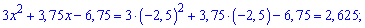
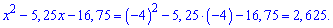
Варто в таких обчисленнях мати під рукою інженерний калькулятор.
Праві сторони рівні, отже x=-2,5 – більший корінь ірраціонального рівняння.
Приклад 3. Розв'язання рівняння
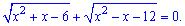
Розв'язання. Знайомтеся із новим типом ірраціональних рівнянь – сума коренів рівна нулю. Розв'язувати їх легше, аніж попередні завдання. А все через одне просте правило. Сума коренів рівна нулю тоді і тільки тоді, коли підкореневі вирази рівні нулю.
Тобто, потрібно розв'язати два квадратні рівняння і вибрати корінь, який є спільним для двох, якщо такий існує. В іншому випадку рівняння розв'язків немає. Оскільки квадратичні функції під коренями не складні, то розв'язки знаходимо через теорему Вієта
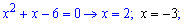
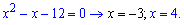
Спільним для двох рівнянь буде x=-3, це і є шуканий розв'язок.
Приклад 4. Визначити суму коренів рівняння
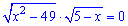 ,
,
які є натуральними числами.
Розв'язання. Маємо добуток коренів рівний нулю. Очевидно, що кожен з коренів потрібно прирівняти до нуля.
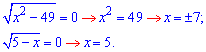
Сумуємо корені 7-7+5=5.
Відповідь:5.
Тут навмисне допущена помилка, тому що така ситуація часто зустрічається на практиці. Всі розв'язують і часто забувають, що вимагалося знайти: суму натуральних чисел (коренів). Тому правильна відповідь – (7+5)=12.
Приклад 5. Визначити найменший розв'язок рівняння
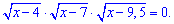
Розв'язання. Прирівнюємо корені до нуля і розташовуємо корені в ряд за зростанням.
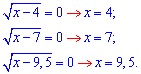
Маємо 4; 7; 9,5. Найменший із знайдених x=4.
Приклад 6. Розв'язання рівняння
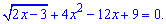
Розв'язання. Не кожен може зразу побачити, що справа міститься підкореневий вираз у квадраті. Тобто
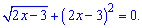
Звідси легко знаходимо розв'язок x=3/2=1,5/ Помилкою в такого роду завданнях є перенесення квадратичної залежності за знак рівності і піднесення до квадрату з подальшими намаганнями, щось спростити та отримати відповідь. Правильним підходом є виділення повного квадрату в квадратичній функції. Це завжди пам'ятайте і використовуйте на практиці.
Приклад 7. Розв'язання рівняння
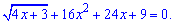
Розв'язання. Ідентичний за методикою розв'язування приклад, тому я записую
4x+3=0; x=-3/4=-0,75,
а Ви спробуйте виділити повний квадрат і розв'язати за наведеною вище схемою.
Приклад 8. Розв'язання рівняння 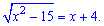
Розв'язання. Досить поширений варіант ірраціональних завдань. Перш за все виписуємо ОДЗ
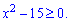
Далі підносимо обидві частини рівняння до квадрату
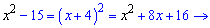
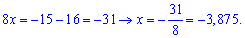
В декого закрадуться сумніви, що квадрат цього числа (-3,875)^2 менший за 15 і рівняння не має розв'язку. Проте, перевірка на калькуляторі показує
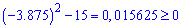
що х=-3,875 є розв'язком ірраціонального рівняння.
Це лиш мала частина прикладів на ірраціональні рівняння, які можна зустріти на тестах при вступі у ВУЗи. Однак на їх базі можна отримати чималий досвід, як не допустити помилок при розв'язуванні ірраціональних рівнянь.
Переглянути схожі матеріали:


