Логарифмом числа b за основою a позначають вираз logab. Обчислити логарифм означає знайти такий степінь x (logab=x), при якому виконується рівність ax=b.
Основні властивості логарифма
Наведені властивості необхідно знати, оскільки, на їх основі розв'язуються практично всі завдання і приклади пов'язані з логарифмами. Решта екзотичних властивостей можна вивести шляхом математичних маніпуляцій з даними формулами
1. logaa=1
2. loga1=0
3. 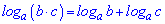
4. 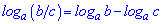
5. 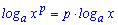
6. 
7. 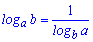
8. 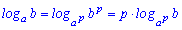
9. 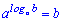
10. 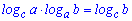
11. 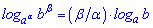
12. 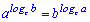
13. 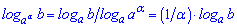
14. 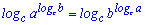
15. 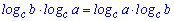
При обчисленнях формули суми та різниці логарифмів (3,4) зустрічаються досить часто. Решта дещо складні, але в ряді задач є незамінними для спрощення складних виразів та обчислення їх значень.
Поширені випадки логарифмів
Одними з розповсюджених логарифмів є такі в яких основа рівна десять, експоненті або двійці.
Логарифм за основою десять прийнято називати десятковим і спрощено позначати lg(x).
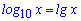
Із запису бачимо, що основи в записі не пишуть. Для прикладу
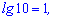
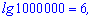
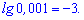
Логарифм натуральний – це логарифм у якого за основу експонента (позначають ln(x)).
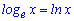
Експонента рівна 2,718281828…. Щоб запам'ятати експоненту можете вивчити правило: експонента рівна 2, 7 і два рази рік народження Лева Миколайовича Толстого. Знаючи це правило будете знати і точне значення експоненти, і дату народження Льва Толстого.
І ще один важливий логарифм за основою два позначають
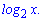
Похідна від логарифм функції рівна одиниці розділеній на змінну
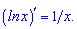
Інтеграл або первісна логарифма визначається залежністю
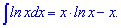
Наведеного матеріалу Вам буде достатньо, щоб розв'язувати широкий клас задач пов'язаних з логарифмами і логарифмуванням. Для засвоєння матеріалу наведу лише кілька поширених прикладів хзі шкільної програми та ВУЗів.
Приклади на логарифми
Прологарифмувати вирази
Приклад 1.
1. х=10ас2 (а>0,с>0).
За властивостями 3,5 обчислюємо
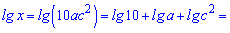
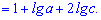
2.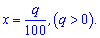
За властивістю різниці логарифмів маємо
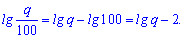
3. 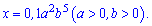
Використовуючи властивості 3, 5 знаходимо
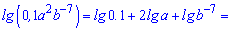
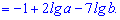
4. 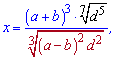 де
де 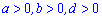 .
.
На вигляд складний вираз із використанням ряду правил спрощується до вигляду
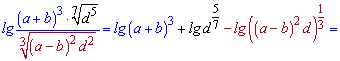
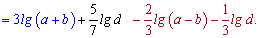
Знаходження значень логарифмів
Приклад 2. Знайти х, якщо
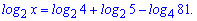
Розв'язання. Для обчислення застосуємо до останнього доданку 5 та 13 властивості
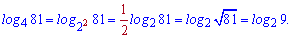
Підставляємо у запис та сумуємо
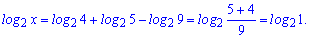
Оскільки основи рівні, то прирівнюємо вирази
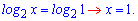
Приклад 3. Нехай задано значення логарифмів
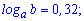
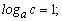
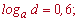
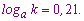
Обчислити log[a](x), якщо 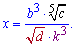
Розв'язання: Логарифмуємо змінну, щоб розписати логарифм через суму доданків
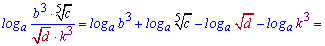
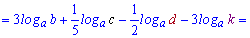
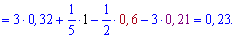
На цьому знайомство з логарифмами та їх властивостями тільки розпочинається. Вправляйтеся в обчисленнях, збагачуйте практичні навики – отримані знання Вам скоро знадобляться для розв'язування логарифмічних рівнянь. Вивчивши основні методи розв'язання таких рівнянь ми розширимо Ваші знання для іншої не менш важливої теми – логарифмічні нерівності...


