Логарифмом числа b по основанию a обозначают выражение 
. Вычислить логарифм значит найти такой степень x (
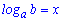),при котором выполняется равенство
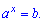
Основные свойства логарифма
Приведенные свойства необходимо знать, поскольку, на их основе решаются практически все задачи и примеры связаны с логарифмами. Остальные экзотических свойств можно вывести путем математических манипуляций с данными формулами
1. 
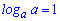
2. 
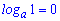
3. 
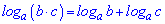
4. 
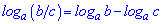
5. 
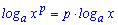
6. 
7. 
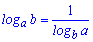
8. 
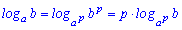
9. 
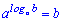
10. 
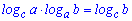
11. 
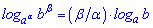
12. 
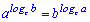
13. 
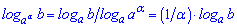
14. 
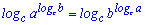
15. 
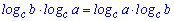
При вычислениях формулы суммы и разности логарифмов (3,4 ) встречаются довольно часто. Остальные несколько сложные, но в ряде задач являются незаменимыми для упрощения сложных выражений и вычисления их значений.
Распространены случаи логарифмов
Одними из распространенных логарифмов такие в которых основание ровное десять, экспоненте или двойке.
Логарифм по основанию десять принято называть десятичным логарифмом и упрощенно обозначать lg(x).
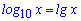
Из записи видно, что основы в записи не пишут. Для примера
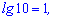
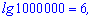
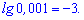
Натуральный логарифм – это логарифм у которого за основу экспонента ( обозначают ln(x)).
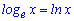
Экспонента равна 2,718281828…. Чтобы запомнить экспоненту можете изучить правило: экспонента равна 2,7 и два раза год рождения Льва Николаевича Толстого. Зная это правило будете знать и точное значение экспоненты, и дату рождения Льва Толстого.
И еще один важный логарифм по основанию два обозначают
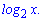
Производная от логарифм функции равна единице разделенной на переменную
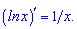
Интеграл или первообразная логарифма определяется зависимостью
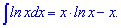
Приведенного материала Вам достаточно, чтобы решать широкий класс задач связанных с логарифмами и логарифмирования. Для усвоения материала приведу лишь несколько распространенных примеров из школьной программы и ВУЗов.
Примеры на логарифмы
Прологарифмировать выражения
Пример 1.
а). х=10ас^2 (а>0,с>0).
По свойствам 3,5 вычисляем
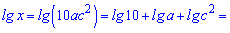
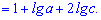
2.
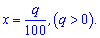
По свойству разницы логарифмов имеем
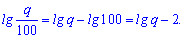
3. 
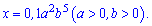
Используя свойства 3,5 находим
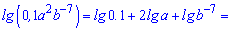
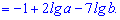
4. 
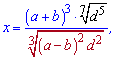где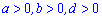 
.
На вид сложное выражение с использованием ряда правил упрощается к виду
------------------------------------------
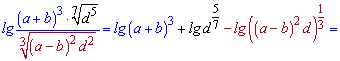
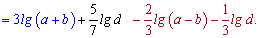
Нахождение значений логарифмов
Пример 2. Найти х, если
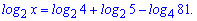
Решение. Для вычисления применим до последнего слагаемого 5 и 13 свойства
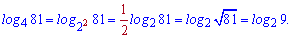
Подставляем в запись и скорбим
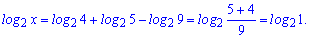
Поскольку основания равные, то приравниваем выражения
------------------------------------------
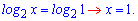
Пример 3. Пусть задано значение логарифмов
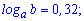
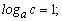
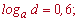
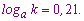
Вычислить log[a](x), если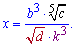 
Решение: Прологарифмируем переменную, чтобы расписать логарифм через сумму слагаемых
------------------------------------------
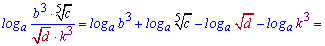
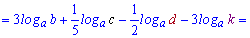
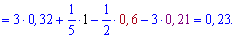
На этом знакомство с логарифмами и их свойствами только начинается. Упражняйтесь в вычислениях, обогащайте практические навыки - полученные знания Вам скоро понадобятся для решения логарифмических уравнений. Изучив основные методы решения таких уравнений мы расширим Ваши знания для другой не менее важной теме - логарифмические неравенства ...
