Знаходити границю функції на контрольній роботі потрібно не тільки на першому, другому курсі вузів, а й в останні роки школярам 11 класів. Серед студентів найбільше дружать з границями математики, механіки, фізики, прикладники, економісти та статисти. Їм наведені нижче завдання контрольної роботи з границь функцій зрозумілі і більшість розв'яже приклади на 5. Та завжди є частина, яка хоче або знати більше або шукає "халяви" в інтернеті. Тому приклади підібрані так, що будуть цікаві для всіх, вони підійдуть і школярам, і студентам.
Приклад 1. Обчислити границю
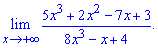Розв'язання: В границі змінна прямує до безмежності, тому в дробовій функції з чисельника і знаменника виносимо змінну в старшому степені та обчислюємо границю
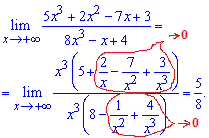
Тут враховано, що доданки в чисельнику і знаменнику, що містять ділення на змінну в 1, 2, 3 степені прямують до нуля при змінній прямуючій до безмежності. Таким чином границя рівна 5/8.
Приклад 2. Обчислити границю
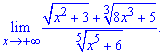Розв'язання: Маємо невизначеність типу безмежність поділити на безмежність 
.
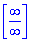Винесемо з чисельника і знаменника змінну х
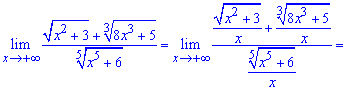
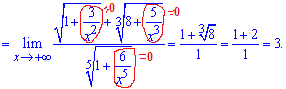
Тут також враховано, що деякі доданки під коренем прямують до нуля холи "ікс" прямує до безмежності.
Приклад 3. Обчислити границю
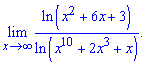Розв'язання: Маємо границю у вигляді частки логарифмів, яка при підстановці дає невизначеність типу безмежність поділити на безмежність
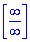. Зробимо наступне перетворення, в чисельнику в логарифмі виділимо множником "ікс" в квадраті, в знаменнику "ікс " в 10 степені та перетворимо згідно властивостей логарифма
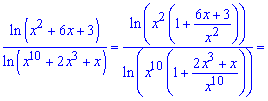
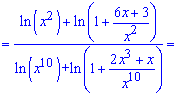
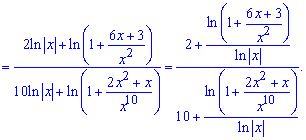
Застосовуючи співвідношення для нескінченно великих функцій і для обчислення границь, отримаємо
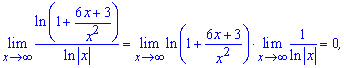
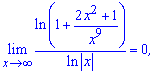
звідси, знаходимо кінцевий вигляд границі
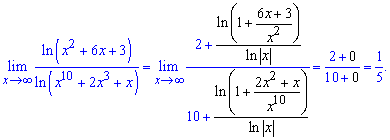
Границя функції рівна 0,2.
Приклад 4. Обчислити границю
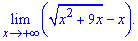Розв'язання: Маємо невизначеність типу безмежність розділити на безмежність 
.
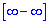Функція має вигляд корінь мінус змінна. Щоб позбутися невизначеності помножимо і розділимо на спряжену функцію
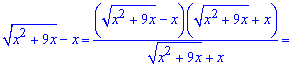
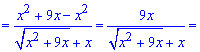
та спростимо чисельник і знаменник на "ікс"
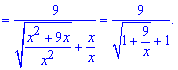
Отримали компактний вираз функції для знаходження границі
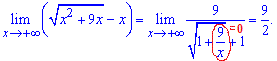
Границя функції рівна 4,5.
Приклад 5. Знайти границю
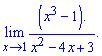Розв'язання: Маємо частку функцій, які дають невизначеність типу нуль поділити на нуль 
. В околі точки х=1 розкладемо функції чисельника і знаменника
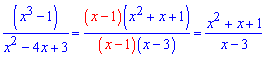
та спростимо на множник, що вносить особливість в границю. Границя функції зведеться до вигляду
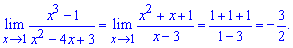
В результаті отримаємо -1,5.
Приклад 6. Обчислити границю
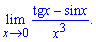Розв'язання: В чисельнику маємо тангенс і синус, в знаменнику "ікс" в кубі. При підстановці отримаємо невизначеність типу нуль поділити на нуль 
.
Винесемо в чисельнику тангенс за дужки та скористаємося формулами для обчислення границь нескінченно малих функцій
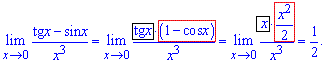
Границя рівна 0,5.
Приклад 7. Обчислити границю
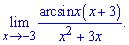Розв'язання: Знову маємо невизначеність типу нуль поділити на нуль 
.
Функція арксинус прямує до нуля при змінній, яка прямує до (-3). Тому застосувавши нескінченно малі функції знайдемо границю
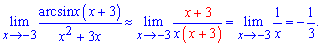
Приклад 8. Знайти границю
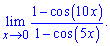Розв'язання: Оскільки косинуси в чисельнику і знаменнику прямують до одиниці коли "ікс" прямує до нуля, то маємо невизначеність виду нуль поділити на нуль. За правилом еквівалентних нескінченно малих функцій замінимо чисельник і знаменник розкладом в околі нуля перших членів ряду
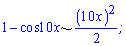
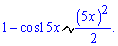
Відшукання границі спроститься до частки
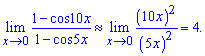
На цьому контрольна робота на знаходження границь функцій розв'язана. Більше завдань на границю Ви можете знайти в категорії "Обчислення границь" з меню вищої математики.
Сподіваюсь приклади на границі були корисними для Вас та частині стануть підказкою на контрольній роботі чи тестах.
