В контрольній роботі містятьться завдання наступного типу: розв'язок СЛАР методом Крамера, границя функції без застосування правила Лопіталя, екстремум функції двох змінних, визначені та невизначені інтеграли, знаходження площі між кривими на площині. Такі задачі часто зустрічаються в студентській практиці та будуть корисні для ознайомлення усім.
Завдання 1. Розв'язати систему трьох лінійних алгебраїчних рівнянь з трьома невідомими за формулами Крамера
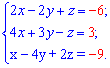
Виконати перевірку розв'язків.
Розв'язання: Знаходимо головний визначник за формулою трикутника
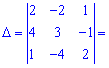
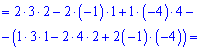
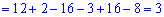
Обчисюємо допоміжні визначники заміною відповідних стовпців на стовпець із вільних членів
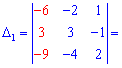
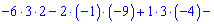
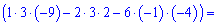
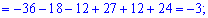
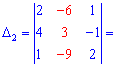
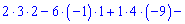
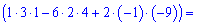
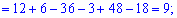
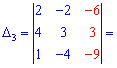
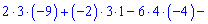
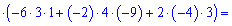
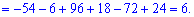
За формулами Крамера обчислюємо розв'язки системи рівнянь
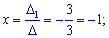
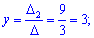
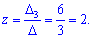
Виконуємо перевірку підстановкою значень
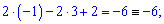
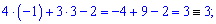
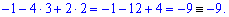
Значення тотожні, отже обчислення виконані правильно.
Завдання 2. Дано координати вершин трикутника А,В,С:
А(3;0), В(5;10), С(13;6).
1) Знайти рівняння сторони АВ.
2) рівняння медіани АМ.
3) рівняння кола, для якого медіана АМє діаметром
Розв'язання:
1) Запишемо умову завдання
АВС: (3;0), В(5;10), С(13;6).
АВ=(5-3;10-0)=(2;10)
Модуль вектора АВ рівний
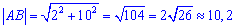
Загальне рівняння прямої, що проходить через точки А і В таке
y=kx+b.
Підставляємо задані точки та зводимо до системи рівнянь
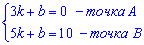
Від другого рівняння віднімаємо перше
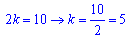
Підставляємо k=5 в друге рівняння
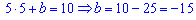
Остаточне рівняння прямої, що проходить через точки А і В таке:
y=5x-15.
2) Знайдемо середину сторони BC, адже медіана АМ буде проходити через цю точку.
М=(B+C)/2;
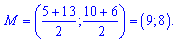
Складаємо рівняння прямої, що проходить через точки
А(3;0); M(9;8);
y=kx+b
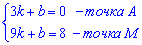
Від другого рівняння віднімаємо перше, помножене на 3
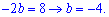
Знайдену невідому підставляємо в перше рівняння
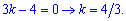
Остаточне рівняння прямої АМ буде наступним
y=4/3*x-4.
3) Знайдемо радіус кола, для якого медіана АМ (А(3;0), M(9;8)) є діаметром
АM=(9-3;8-0)=(6;8);
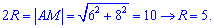
Знайдемо центр кола – точку О.
O=(A+M)/2;
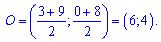
Рівняння кола з центром в точці О(6;4) та радіусом 5 буде наступним.
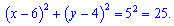
Трикутник та коло наведені нижче
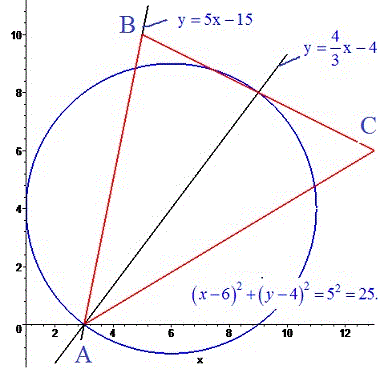
Завдання 3. Знайти границі функцій, не користуючись правилом Лопіталя:
а)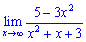 
Розв'язання: При змінній прямуючій до безмежності домінуючий вклад вносять доданки, в яких змінна міститься в більшому степені. Виносимо їх за дужки та скорочуємо
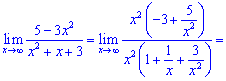
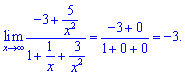
б)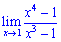 
Розв'язання: Чисельник і знаменник перетворюються в нуль у точці x=1. В подібних випадках потрібно скоротити обидві частини на множник, що має особливість. В данному випадку можна було скористатися формулами
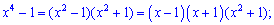
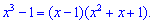
Але такими формулами можна скористатися лише в окремих випадках. В загальному, якщо функція має вигляд поліном розділити на поліном, і вточці знаходження границі x0 обидві перетворюються в нуль то необхідно їх розділити на (x-x0). В даному випадку отримаємо такі розклади для чисельника
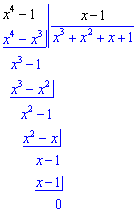
та знаменника відповідно.
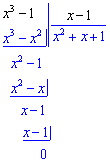
Отримані значення підставляємо в границю та обчислюємо
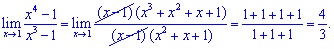
Границя функції рівна 4/3.
Завдання 4. Знайти похідну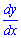 
функції
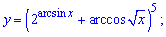
Розв'язання: Знаходимо похідну за правилом складеної функції. Спершу від степеневої функції за формулою
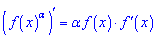
а далі від фукцій в дужках.
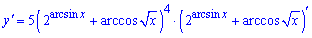
В останній дужці похідну шукаємо від кожного доданку окремо.
До першого доданку застосовуємо логарифмічне диференціювання
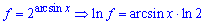
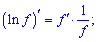
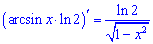
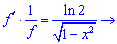
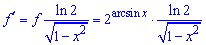
Другий доданок внесе такий вклад
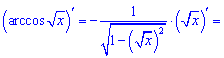
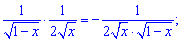
Підставляємо знайдені значення в похідну
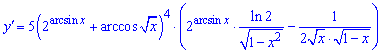
Даний приклад навчить Вас нових прийомів, тому добре в ньому розберіться.
Завдання 5. Дослідити функцію z=f(x,y) на екстремум:
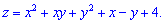
Розв'язання: Методика дослідженя функції двох змінних на екстремум наступна.
Знаходимо похідні dz/dx і dz/dy та пирівнюємо їх до нуля.
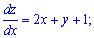
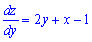
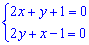
Розв'язавши систему рівнянь знайдемо екстремальну точку.
З другого рівняння виражаємо невідому х та підставляємо в перше.
х=1-2y
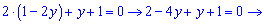
3-3y=0
y=1.
Знайдене значення підставляємо в будь-яке із рівнянь (2)
Отже точка А(-1;-1) точка екстремуму.
Знайдемо другі похідні
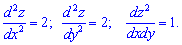
За необхідною ознакою екстремуму знаходимо
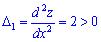
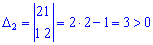
Оскільки обидва додатні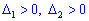 
, то точка А(-1;1)є точкою мінімуму.
Графічно функції в околі мінімуму зображено нижче
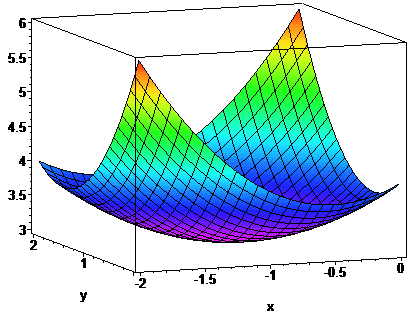
Завдання 6. Знайти невизначені інтеграли:
а)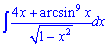 
Розв'язання: Розбиваємо підінтегральний вираз на два доданки та знаходимо невизначені інтеграли. Перший інтеграл знаходимо заміною змінних, другий - внесенням змінної під диференціал.
1) 
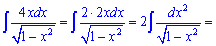
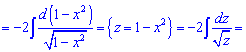
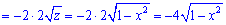
2) 
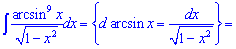
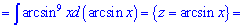
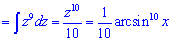
Сумуємо інтеграли
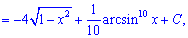
де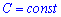
- константа. На цьому всі розрахунки.
б)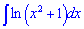 
Розв'язання: Даний інтеграл обчислюємо за правилом інтегрування частинами udv
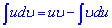
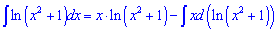
Знаходимо інтеграл, що залишився
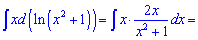
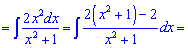
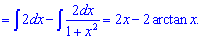
Підставляємо вираз у вихідний інтеграл
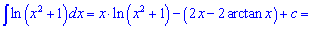
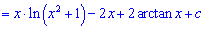
У відповіді отримали і логарифм і арктангенс.
Завдання 7. Обчислити визначений інтеграл
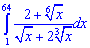
Розв'язання:Проведемо деякі перетвореня підінтегральної функції
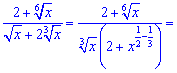
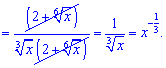
після чого виконаємо інтегрування
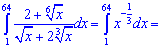
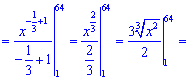
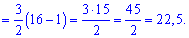
Інтеграл рівний 22,5.
Завдання 8. Обчислити площу фігури, обмеженої лініями:
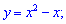
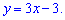
S-?
Розв'язання: Знайдемо точки перетину цих ліній
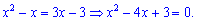
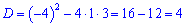
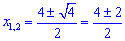
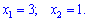
Для з'ясування, яка крива знаходиться вище на графіку, а яка нижче підставляємо точку з проміжку [1;3], наприклад візьмемо точку х=2
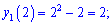
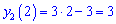
Обидві функції на графіку матимуть такий вигляд
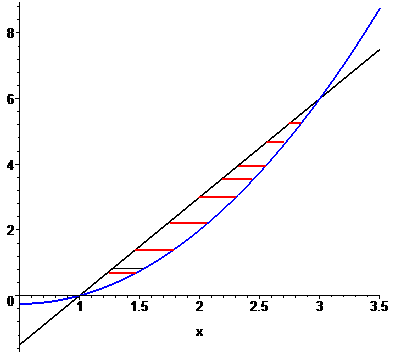
Отже друга лінія вище на графіку від першої, враховуючи це знаходимо площу
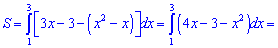
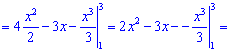
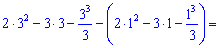
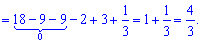
Якщо не враховувати порядку кривих то може вийти від'ємне значення інтегралу. Пам'ятайте, що площа від'ємною не буває (міняйте знак при відповіді).
Вибирайте для себе простіші та швидкі методи обчислення тих чи інших завдань. Практикуйте та не майте труднощів у подібних обчисленнях.
