Готові відповіді контрольних чи індивідуальних робіт, зокрема із теорії ймовірностей люблять усі студенти, особливо коли якісно пояснені обчислення. Наведені нижче завдання задавали в Львівському національному університеті імені Івана Франка, на якому факультеті ми Вам не скажемо. Готових завдань по рядах тут вдосталь, щоб підготуватись до контрольної чи тестів.
Завдання: 1.3 Обчислити суму рядів:
а)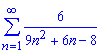 
Розв'язання: Спершу виконуємо перевірку ряду на збіжність
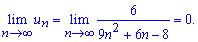
Границя загального члена ряду рівна нулю, отже даний ряд збігається. Якщо Ви отримаєте границю відмінну від нуля, хоча і скінченну, то такий ряд буде розбіжним, а його сума рівна плюс або мінус безмежності. Тобто такі ряди не сумують. На екзаменах, як правило такі приклади не зустрічаються, однак на тестах можливо все. Тому перш ніж переходити до сумування ряду перевіряйте його на збіжність.
Напряму Ви суму цього ряду оцінити не зможете, єдиний вихід розкласти знаменник загального члена ряду на прості множники, а далі методом невизначених коефіцієнтів сам дріб звести до різниці найпростіших дробів
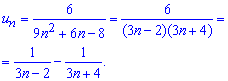
Це дасть можливість звести обчислення суми ряду до відшукання різниці двох рядів
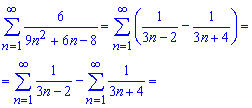
Якщо останні розписати в явному вигляді, то завжди отримаєте, що більшість доданків при обчисленні дасть нуль (підкреслені). Решта, що залишилися (виділені чорним) і є шуканою сумою ряду
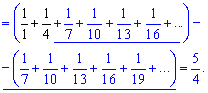
Тепер Ви на крок ближче, щоб самостійно знайти суму ряду.
б)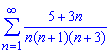 
Розв'язання: Знаходженням границі
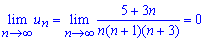
переконуємося, що вона рівна 0, а заданий ряд збігається.
Далі методом невизначених коефіцієнтів розкладаємо загальний член ряду на прості дроби
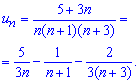
Це дозволяє перейти від обчислення суми 1 складного ряду до сумування 3 простих рядів
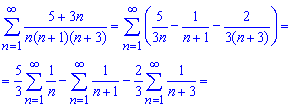
Ряди записуємо у явному вигляді і виділяємо доданки, що знищаться при сумуванні
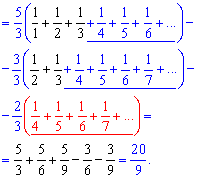
Підказкою слугує те, що члени одного з рядів (виділений червоним) в кінцеву суму жодного вкладу не внесуть. Також для зручності обчислень записуйте ряди один під одним. Для чого це потрібно Ви можете бачити з цього прикладу.
Завдання: 2.4 Дослідити збіжність рядів:
а)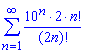 
Розв'язання: Заданий ряд має додатні члени, тому можемо дослідити збіжність ряду за ознакою Даламбера:
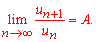
Записуємо члени ряду, що фігурують в границі
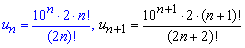
та підставляємо у формулу Даламбера
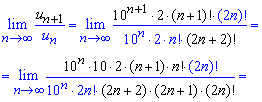
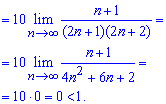
При розписуванні границі найбільше помилок в студентів виникає при розписуванні факторіалів, тому добре вивчіть властивості факторіалів.
Оскільки границя менша одиниці A=0<1, то даний ряд збігається!
б)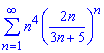 
Розв'язання: Досліджувати на збіжність ряд будемо за ознакою Даламбера. Для цього записуємо формули загального члена ряду та наступного після нього
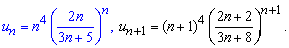
Далі підставляємо їх у границю та, наскільки це можливо, спрощуємо її
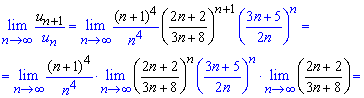
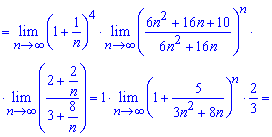
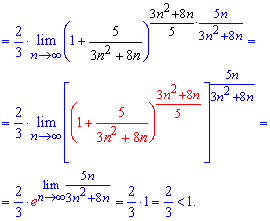
При обчисленні один з множників під границею рівний другій чудовій границі – експоненті.
Оскільки границя менша одиниці A=2/3<1, то робимо висновок про збіжність ряду.
Завдання: 3.5 Знайти радіус збіжності та область збіжності степеневих рядів:
а)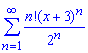 
Розв'язання: Заданий функціональний ряд може при певних значеннях змінної приймати від'ємні значення, тому для дослідження збіжності ряду за ознакою Даламбера
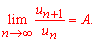
складемо ряд із модулів членів заданого ряду
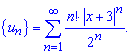
Записуємо загальний та наступний після нього члени ряду з модулів
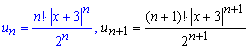
та підставляємо їх у границю
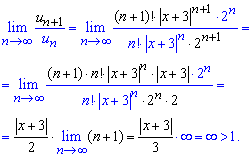
Розписавши факторіали та степеневі залежності, прийдемо до залежності, яка не є обмеженою. Границя рівна безмежності, отже функціональний ряд розбігається (за теоремою Даламбера) при всіх дійсних значеннях змінної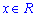 
.
Це означає, що радіус збіжності рівний нулю R=0, а область збіжності порожня множина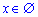 
.
б)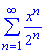 
Розв'язання: Складемо ряд із модулів членів заданого ряду:
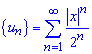
а далі виконуємо дослідження ряду на збіжність за теоремою Даламбера.
Знаходимо границю частки старшого та молодшого членів функціонального ряду
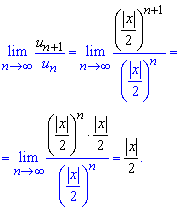
За теоремою Даламбера ряд збігається для змінних, що задовільняють умову
.
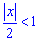Розкриваючи модуль знаходимо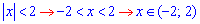 
область збіжності ряду та записуємо радіус збіжності R=2.
Завдання: 4.6 Розкласти дробову функцію в ряд по степенях x:
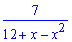
Розв'язання: Розкладемо функцію методом невизначених коефіцієнтів на суму простих дробів, а далі перетворимо знаменники, щоб мати зручний запис для розкладу
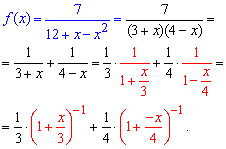
Функцію f(x) розкладемо в ряд за степенями x, скориставшись формулами Маклорена для степеневих функцій:
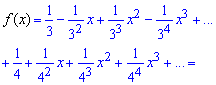
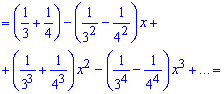
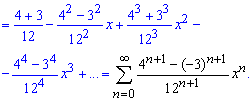
Вкінці згрупуємо доданки при однакових степенях "ікс" та розклад функції записуємо рядом.
Завдання: 5.7 Розкласти арктангенс функцію в ряд по степенях x:
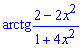
Розв'язання: Для розкладу арктангенса застосуємо наступну методику. Спершу знайдемо похідну складеної функції від арктангенса
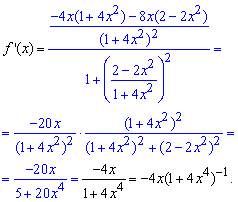
Розкладемо похідну арктангенса в ряд за степенями x, використовуючи формули Маклорена
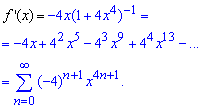
Щоб отримати розлад арктангенса інтегруємо похідну. Враховуючи, що f(0)=arctg(2), отримаємо ряд за степенями x заданої функції f(x):
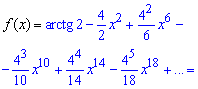
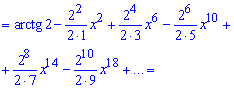
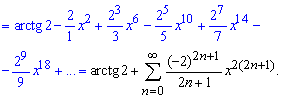
Останній перехід до ряду не такий очевидний, однак для знакозмінного ряду саме такі залежності отримують у відповідях.
Завдання: 6.8 Розкласти функцію в тригонометричний ряд Фур'є:
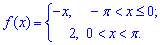
Розв'язання:Схема розкладу в ряд Фур'є детально розписана в попередніх статтях. Тут інтегруванням визначаємо коефіцієнти Фур'є:
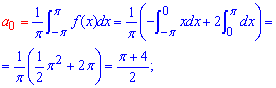
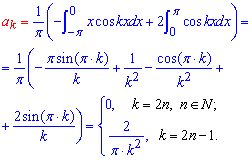
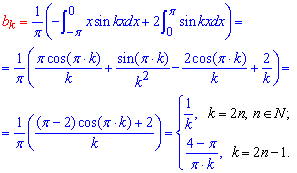
Далі для заданої функції ряд Фур'є відповідно до формул матиме вигляд
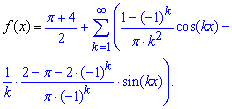
В кінцевому розкладі функції коефіцієнти Фур'є для непарних та парних індексів об'єднали в один. В цьому, як і в інтегруванні вся суть розкладу функції в тригонометричний ряд. Ось такі завдання з теорії рядів Вам доведеться вирішувати на контрольній чи екзаменах. Якщо сумніваєтеся у власних силах, то замовляйте обчислення у нас!
